1. Цель работы: изучение метода статистических испытаний.
2. Исходные данные для расчета:
![]()
![]() Ом - нормальный закон
распределения
Ом - нормальный закон
распределения
![]() - нормальный закон
распределения
- нормальный закон
распределения
![]() - равномерный закон
распределения
- равномерный закон
распределения
![]() - равномерный закон
распределения
- равномерный закон
распределения
![]()
3. Пример расчета и таблица результатов
Для закона нормального
распределения с параметрами ![]() ,
, ![]() , случайные величины ui получают при помощи линейного
преобразования:
, случайные величины ui получают при помощи линейного
преобразования:
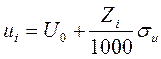 , где U0 – номинальное значение величины,
, где U0 – номинальное значение величины, ![]() -
нормально распределённые случайные числа,
-
нормально распределённые случайные числа,![]() -
стандарт, рассчитываемый по правилу трех сигм:
-
стандарт, рассчитываемый по правилу трех сигм:
![]() , где
, где ![]() -
половина поля допуска.
-
половина поля допуска.
Для![]() Ом:
Ом:
![]() Ом
Ом
![]() Ом
Ом
![]() Ом
Ом
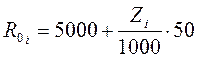
При ![]() =464 имеем:
=464 имеем:
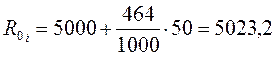 Ом
Ом
Для![]() :
:
![]()
![]()
![]()
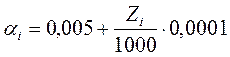
При ![]() =464 имеем:
=464 имеем:
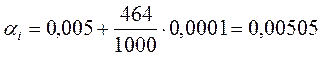
Для равномерного закона случайные величины ui, равномерно распределенные в интервале от а до b, получают при помощи линейного преобразования:
![]() , (3)
, (3)
где 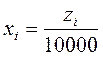 ,
, ![]() - равномерно распределённые случайные числа,
а – минимальное значение величины, b – максимальное значение величины.
- равномерно распределённые случайные числа,
а – минимальное значение величины, b – максимальное значение величины.
Для ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
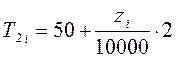
При ![]() =1009 имеем:
=1009 имеем:
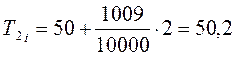
![]()
Для ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
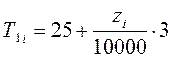
При ![]() =1009 имеем:
=1009 имеем:
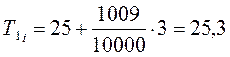
![]()
Для всех полученных выше значений рассчитываем значение случайной величины R:
![]() Ом
Ом
Расчет номинального значения величины R:
![]() Ом
Ом
Допуск составляет ![]() , где 2% от номинального значения:
, где 2% от номинального значения: ![]() Ом
Ом
Тогда
![]() .
.
Рассчитанное значение случайной величины R попадает в этот интервал.
Для определения вероятности попадания случайной величины R в заданный интервал необходимо произвести большое число опытов(30 – в нашем случае), тогда частота Р* будет стремиться к искомой вероятности P с ошибкой:
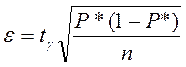 , где
, где ![]() -
параметр распределения Стьюдента, определяемый доверительной вероятностью(
-
параметр распределения Стьюдента, определяемый доверительной вероятностью(![]() ) и числом опытов(n=30).
) и числом опытов(n=30).
![]()
Таблица результатов для 30 опытов:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.