Соотношения между электрофизическими характеристиками двух образцов по известным диаграммам температурной зависимости электропроводности

Федеральное агентство по образованию Российской Федерации

Государственное образовательное учреждение

высшего профессионального образования

Владимирский государственный университет

Кафедра конструирования и технологии радиоэлектронных средств

лабораторная работа

по дисциплине: «Физические основы микроэлектроники»

Выполнил:

студент гр. Р-105

Руководитель:

Владимир 2007

1.1 Формулировка задачи

Определить соотношения между электрофизическими характеристиками двух образцов по известным диаграммам температурной зависимости электропроводности.

1.2 Краткие теоретические сведения

Проводимость полупроводника обусловлена концентрацией свободных носителей (электронов в зоне проводимости или дырок в валентной зоне)  и величиной их подвижности:

,                                                      (1.1)

где  - концентрация свободных носителей;

 - подвижность носителей;

- подвижность электронов;

 - подвижность дырок;

 - заряд электрона.

Концентрация носителей зависит от температуры. Для примесной проводимости концентрация носителей (n - электронов, p- дырок) определяется следующим выражением:

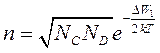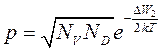,                                        (1.2)

где - эффективная плотность состояний для электронов;

- эффективная плотность состояний для дырок;

-  концентрация примесных атомов;

 - энергия активации донорных атомов;

- энергия активации акцепторных примесей;

k- постоянная Больцмана;

Т – абсолютная температура.

Концентрация собственных носителей:

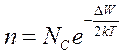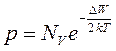 ,                                                (1.3)

где - ширина запрещённой зоны.

Из выражений (1.1), (1.2) следует, что проводимость примесного полупроводника:

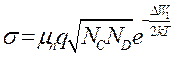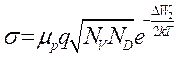,  ,                                 (1.4)

проводимость собственного полупроводника:

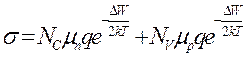.                                          (1.5)

Подвижность определяется рассеянием носителей на примесях  и тепловых колебаниях решётки. По мере увеличения температуры до определённых пределов подвижность плавно возрастает по закону:

.                                                         (1.6)

При дальнейшем росте температуры усиливаются процессы фонон-электронного взаимодействия, вследствие этого подвижность уменьшается по закону:

.                                                        (1.7)

Таким образом, проводимость полупроводниковых материалов сильно зависит от температуры, при этом определяющей является температурная зависимость концентрации носителей.

1.3 Решение задачи

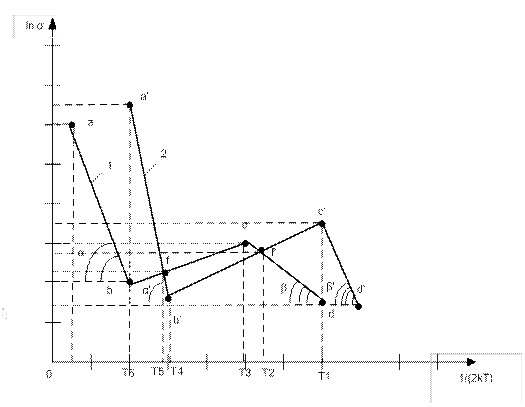
Рис.1.1. Температурные зависимости электропроводности образцов 1 и 2 полупроводниковых материалов при высоких (участки a-b и a_’-b_’) и низких (участки c-d и c’-d’) температурах.

Зависимость проводимости полупроводника от температуры можно представить в виде трех участков на графике: правая часть (область низких температур) - электропроводность определяется примесной составляющей, этому участку соответствует выражение (1.4); средняя часть - снижение величины электропроводности в результате уменьшения подвижности, соответствует выражение (1.7), левая часть (область высоких температур) - примесная проводимость переходит в собственную и резко возрастает, выражение (1.5).

Тангенс угла наклона участка ab к оси абсцисс равен ширине запрещенной зоны ΔW, не зависящей от концентрации примесей. Наклон участка cd к оси абсцисс определяет энергию активации донорного уровня ΔW₁.

Энергия активации донорного уровня будет иметь следующее соотношение:

                                                          (1.8)

Получается, что

                                                                   (1.9)

Рассмотрим область низких температур. Фиксируем значение Т₁. При этом значение температуры, значение проводимости второго образца больше проводимости первого:

                                                                 (1.10)

Подставляя выражение (1.1) в неравенство получаем:

                                                                    (1.11)

В первом образце при температуре Т₁ происходит процесс ионизации атомов примеси, во втором образце – все атомы примеси уже ионизированы.

Подставляя в неравенство выражение (1.4) и сократив элементарный заряд, получаем:

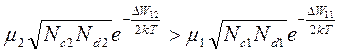                                   (1.12)

Если предположить, что подвижности носителей в образцах равны:

                                                                 (1.13)

Учитывая выражения (1.9) и (1.13) получаем следующее неравенство:

                                            (1.14)

Эффективная плотность состояний одинакова, то можно сделать вывод:

                                                             (1.15)

Концентрация примеси во втором образце больше концентрации примеси в первом.

При дальнейшем увеличении температуры до Т₂ графики пересекаются в точке f^’. Это означает, что значение проводимости образцов при этой температуре равны:

                                                                 (1.16)

В первом образце при температуре Т₂ происходит процесс ионизации атомов примеси. Подставляя выражение (1.1) и (1.4) проводимость равна: