




























ОПТИКА
Геометрическая оптика как предельный случай волновой оптики. Распространение света рассматривается как движение световой энергии по лучам. Плоскость, перпендикулярная лучам света называется волновым фронтом. Приближение геометрической оптики, это переход от уравнений, описывающих волны к уравнениям, описывающим лучи.
В геометрической оптике не учитывается эффекты дифракции.
В геометрической оптике все лучи от точки предмета идут по различным путям и встречаются в точке изображения. Но все они затрачивают одно и тоже время на прохождение своего пути. Другими словами: оптические длины всех путей, соединяющих точку предмета с точкой изображения, одинаковы. Это утверждение называется принципом таутохронизма.
Законы отражения и преломления. 1. Частота электромагнитной волны
при отражении и преломлении не изменяется: ![]() .
.
|
Рис. 28. Преломление света при п2 > n1 |
2. Волновые векторы (лучи) падающей, отраженной и преломленной волны
лежат в одной плоскости. Если:![]() то
то ![]() , где
, где ![]() - вектор
с началом отсчета в плоскости раздела сред, перпендикулярной вектору.
- вектор
с началом отсчета в плоскости раздела сред, перпендикулярной вектору.
3. Угол падения равен углу отражения: ![]() .
.
Принцип Ферма. Принцип Ферма может быть высказан в форме утверждения, что лучом, соединяющим две точки, является тот путь, который делает стационарным время, затрачиваемое светом на его прохождение.
|
Рис. 29. К выводу законов преломления с помощью принципа Ферма |
Он был открыт П. Ферма (1601-1665 гг.) в 1657 г. как “принцип наименьшего времени” в такой формулировке: “Природа всегда следует по наикратчайшему пути”. Наикратчайших путей может существовать много. В геометрической оптике все лучи от точки предмета идут по различным путям и встречаются в точке изображения. Но все они затрачивают одно и то же время на прохождение своего пути.
Соединим лучом точки Р1 и Р2 находящиеся в однородных средах с показателями преломления n1 и n2и разделенных плоской границей (рис. .). Полное время распространения света из Р1 в Р2:
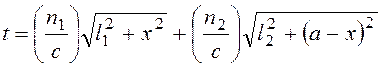 , где
, где 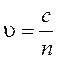 зависит
от переменной х.
зависит
от переменной х.
Условие стационарности 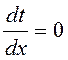 принимает вид
принимает вид
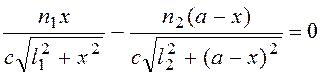 ;
;
Учитывая, что 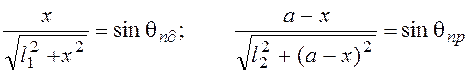 получаем
получаем ![]() ,
что совпадает с законом Снелла.
,
что совпадает с законом Снелла.
Отношение синуса угла падения к синусу угла преломления равно показателю
преломления среды с преломленным лучом относительно среды с падающим лучом.
Показатель преломления ![]() второй среды относительно первой
называется относительным показателем преломления. Если одна из сред вакуум, то
второй среды относительно первой
называется относительным показателем преломления. Если одна из сред вакуум, то 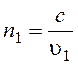 и
и 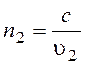 -
абсолютные показатели преломления сред 1 и 2 относительно вакуума.
-
абсолютные показатели преломления сред 1 и 2 относительно вакуума.
4. Полное внутреннее отражение (n2< n1). Видя,
что при некотором значении, называемом предельным углом угол преломления
становится равен ![]() , т.е. преломленный луч движется
вдоль поверхности раздела и нет никакого преломленного луча во второй среде
(рис. 30, а, б).
, т.е. преломленный луч движется
вдоль поверхности раздела и нет никакого преломленного луча во второй среде
(рис. 30, а, б).
|
а б Рис. 30. Преломление свeтa при п2 < n1 (а). При предельном угле падения (б) угол преломления становится равным π/2 |
5. а) При отражении света от границы со среды с большим показателем преломления (n2 > n1) фаза отраженной волны изменится на p, т.е. вектор напряженности электрического поля (магнитного поля) изменяет направление на обратное.
б) При отражении света от границы со средой с меньшим показателем
преломления не происходит изменения фазы вектора ![]() .
.
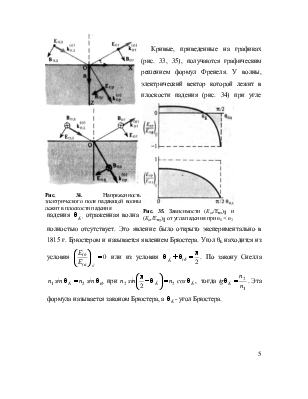
(в) Преломленная волна в обоих случаях не претерпевает изменения фазы.
|
Рис. 31. Разложение плоской волны на две волны, поляризованные во взаимно перпендикулярных плоскостях |
Рассмотрим содержание закона 5, более подробно. Плоскость, в которой лежит вектор падающей волны и нормаль к поверхности раздела в точке падения луча, называется плоскостью падения луча. Будем обозначать с индексом || компоненты векторов, лежащих в плоскости
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.