Разработка лабораторного макета, при помощи которого можно исследовать помехоустойчивость и оценить верность передачи информации, страница 2

1.  Среднеквадратичная функция потерь представленная на рис.1.

 

При этом выражение для  среднеквадратичной ошибки имеет вид:

 

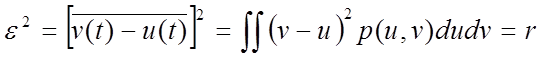Разность  v(t) – u(t)  можно рассматривать как «помеху» на выходе приемника. Если канал имеет идеальную П-образную частотную характеристику, то при наличии флуктуационной помехи с равномерным  спектром  расхождение   между  u  и  v  на  частоте              будет равно интенсивности помехи на выходе приемника на этой частоте                                                     

а среднеквадратичное расхождение за счет всех составляющих определится средней мощностью помехи на выходе приемника          .

         Относительная ошибка определится как выражение:

 

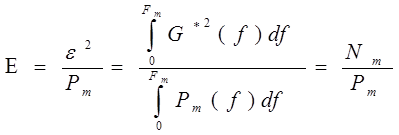Где Fm – полоса пропускания приемника по низкой частоте.                                             

Pm – средняя мощность сигнала на выходе приемника.

 Таким образом, квадрат среднеквадратичной ошибки полностью определяется средней мощностью помехи на выходе приемника, а относительная ошибка – отношением средней мощности помехи Nm к средней мощности сообщения Pm

Вместо величины Е удобно пользоваться логарифмической мерой точности воспроизведения:

 

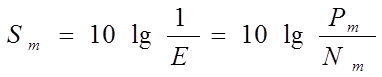Величина Sm численно равна отношению сигнала к помехи на выходе приемника, выраженному в децибелах.

Для практических расчетов в качестве критерия помехоустойчивости часто принимают величину  “ выигрыша системы   [  ]”.

B = Sm / S,

где Sm = Pm / Nm – отношение средних мощностей сигнала и помехи  на выходе,  а  S = P/N – на входе приемника.

          2. Средняя по модулю функция потерь P (u,v) = | V – U |, для которой средняя по модулю ошибка будет иметь следующий вид:

График этой функции представлен на рис. 2

3. Прямоугольная функция потерь

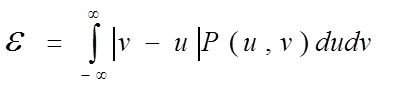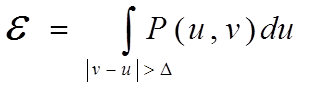Прямоугольная функция потерь, ее график, представлена на рис. 3.

В данном дипломном проекте для оценки верности передачи непрерывных сообщений будем использовать среднеквадратичную функцию потерь. Это подразумевает то, что среднеквадратичное расхождение за счет всех составляющих на выходе приемника будет полностью определяться средней мощностью шума на выходе приемника. То есть оценка верности будет определяться путем сравнения принятого и задержанного переданного сигналов, при чем, если принятый сигнал верный, то значение средней мощности шума на выходе блока сравнения не изменится. В противном случае значение средней мощности шума на выходе увеличится за счет ошибки в принятом сигнале, что можно зафиксировать с помощью стрелочного индикатора, нулевое значение которого соответствует значению средней мощности шума при условии, что принятый сигнал верный. Если принятый сигнал является ортогональным для переданного, то стрелочный индикатор будет показывать максимальное значение. Таким образом в лабораторной работе необходимо будет снять зависимость среднеквадратичной ошибки приема от отношения сигнал шум на входе приемника. Уровень шумов будет изменяться при помощи регулируемого генератора шума, а стрелочный индикатор будет показывать средний квадрат ошибки.  

4.2 Оценка верности передачи дискретных сообщений

Критерий помехоустойчивости [ ] записан применительно к системам передачи непрерывных сообщений U(t). Для систем передачи дискретных сообщений этот критерий определяется следующим выражением:

 

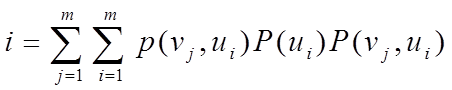Простая функция потерь в этом случае:

 

 При этом согласно [1] средний риск:

 

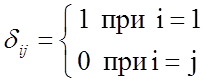
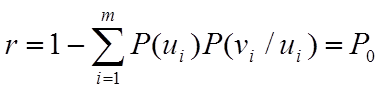где P0 – среднее вероятность ошибок. Таким образом, вероятность передачи любой системы связи можно оценивать величиной среднего риска.

При передаче дискретных сообщений в случае простой функции потерь средний риск равен средней (полной) вероятности ошибок [8].

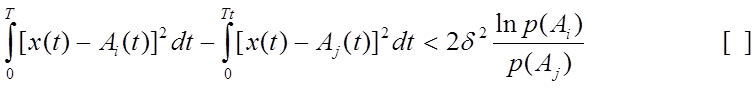Определим вероятность ошибки в системе передачи бинарных сигналов. Пусть сигнал может принять значение  А1(t)  с вероятностью  P(A1) и значения   А2(t)с вероятностью P(A2). Согласно:

                                                                                                                     приемник будет воспроизводить сообщение, соответствующее сигналу  A1(t) если выполняется неравенство:

 

и сигналу                в противном случае. Если был передан сигнал                   , то вероятность ошибки будет равна вероятности выполнения неравенства. Подставим значение X(t) в неравенство и раскроем скобки. После сокращения получаем:

 

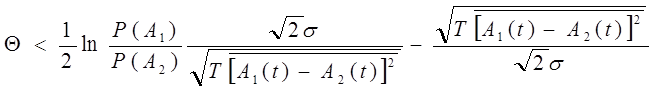Вероятность выполнения этого неравенства может быть определена по формуле.

Вероятность ошибочного приема при передаче сигнала                 :

 

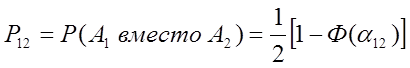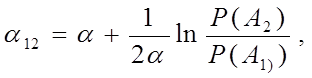Где

 

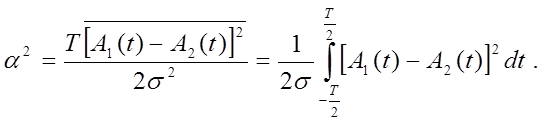Совершенно аналогично определяется вероятность ошибки при передаче сигнала A1(t)

 

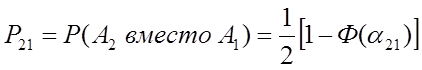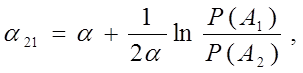Где,

Вероятность  ошибки при идеальном приеме бинарных сигналов A1(t) и А2(t):

                                                                                                                                   либо:

 

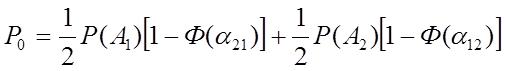Из формул видно, что вероятность ошибки определяющая потенциальную помехоустойчивость зависит от двух величин    и  Р(А1)/P(A2).  

Первая величина определяется отношением удельной энергии разности сигналов к интенсивности помехи          . Чем больше это отклонение, тем больше потенциальная помехоустойчивость. Отношение априорных вероятностей Р(А1)/Р(А2) определяется статистическими свойствами передаваемых сообщений.

Если передаваемые сигналы равновероятны Р(А1)=Р(А2)=1/2 то вероятность ошибки будет иметь вид:

Р0=1/2 [1 – Ф(a)]

При малой интенсивности помех, когда  a >>1 в формулах вторым членом можно пренебречь. Вероятность ошибки при этом практически не зависит от Р(А1) и Р(А2).

При большом уровне помех, когда a мало, зависимость вероятности ошибки от отношения априорных вероятностей Р(А1) и Р(А2) становится заметной. Отклонение этого отношения от единицы приводит к увеличению вероятности ошибок [2]. Таким  образом, при равновероятных сигналах вероятность ошибки полностью определяется величиной a. Значение этой величины зависит от передаваемых сигналов А1(t) и А2(t).