1. Задание на расчёт
С
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Дана
RC – цепь
Дана
RC – цепь
R
R=1 кОм С=1 мкФ
![]()

![]()
![]()
![]()

![]()
![]() Е
Е
Е
Е
τ t Т/2 Т t
![]()
1. Рассчитать следующие характеристики цепи : АЧХ , ФЧХ , импульсную характеристику , переходную характеристику , построить соответствующие графики.
2. Разложение в ряд Фурье для периодического сигнала. Просуммировать на периоде первые 5 членов этого ряда , построить соответствующий график.
3. Для непериодического сигнала найти выражение спектральной плотности , АЧХ и ФЧХ , соответствующие графики.
4. Найти отклик цепи на периодический сигнал. Записать выражение ряда Фурье для сигнала на выходе цепи , и просуммировать первые 5 членов этого ряда, соответствующий график.
5. Отклик цепи на непериодический сигнал.
2. Коэффициент передачи цепи, её АЧХ и ФЧХ
Rвх = R+1/jωC Rвых = R
K(jω)=
Rвых
/Rвх =
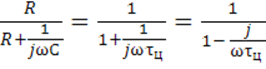 , или , представив в экспоненциальной форме , получим :
, или , представив в экспоненциальной форме , получим :
K(jω)= 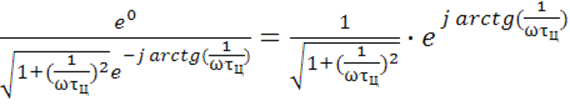
Подставив конкретные значения , получим :
![]() =R
=R![]() C=
C=![]()
K(jω)=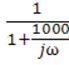 ; в экспоненциальной форме K(jω)=
; в экспоненциальной форме K(jω)=
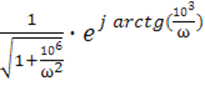
Где АЧХ цепи 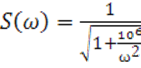 , ФЧХ цепи :
, ФЧХ цепи : ![]()
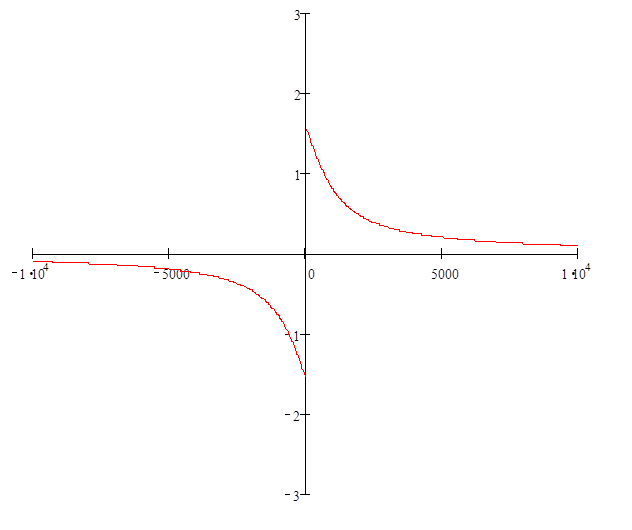
3. Импульсная и переходная характеристики цепи
Импульсная характеристика цепи – это её отклик на дельта функцию , вычисляется по формуле:
![]() , этот интеграл будем вычислять с
помощью обратного преобразования Лапласса :
, этот интеграл будем вычислять с
помощью обратного преобразования Лапласса :
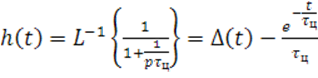 , подставив данные получим :
, подставив данные получим :
![]() . Как видим , в выражении
присутствует дельта функция-
. Как видим , в выражении
присутствует дельта функция- ![]() .
.
![]()
![]()
![]()
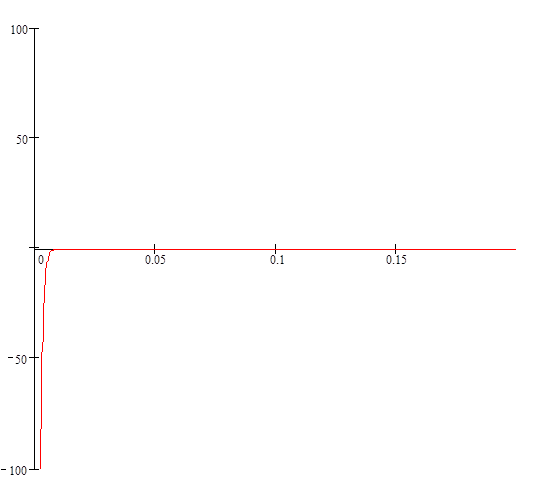
Переходная характеристика цепи вычисляется по формуле :
![]() . Вычисляем с помощью обратного
преобразования Лапласса :
. Вычисляем с помощью обратного
преобразования Лапласса :
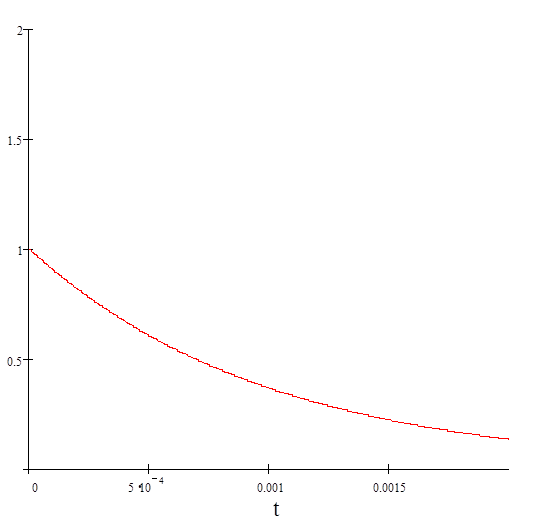
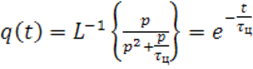 , и ,подставив конкретные
значения, получим:
, и ,подставив конкретные
значения, получим:
![]() .
.
![]()
![]()
![]()
4. Разложение периодического сигнала в ряд Фурье
Аналитически сигнал можно представить в виде : ![]()
Найдём коэффициенты ряда Фурье :
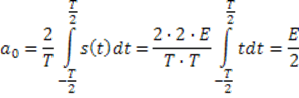
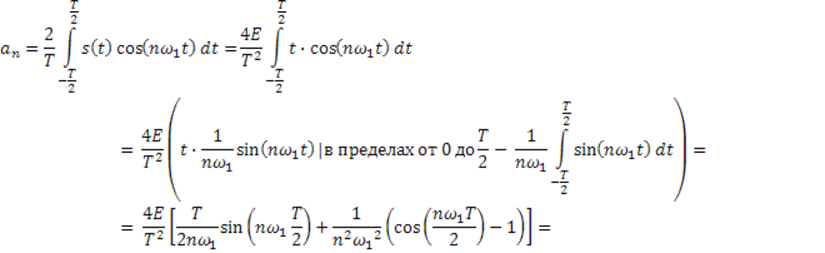
![]()
![]() ,
т.к.
,
т.к.
![]()
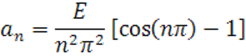
Аналогично для ![]() :
:
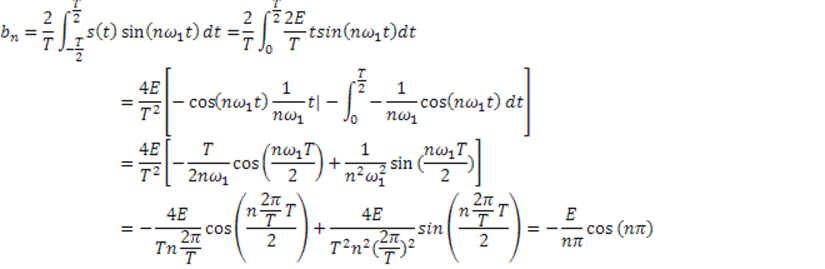
Таким образом : ![]()
Вычислим первые 5 членов ряда Фурье :
![]()
![]()
Сигнал с помощью ряда Фурье можно представить так :
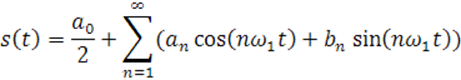
Или же
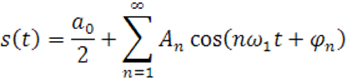
Где:
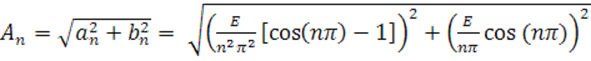 ,
,
![]() =
=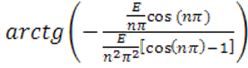 =
=![]() ,
,
Таким образом сигнал можно представить в виде :
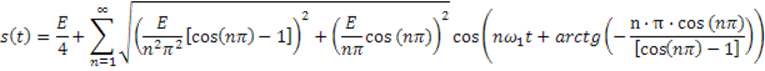
Вычислим первые 5 членов второго ряда :
![]()
![]()
![]()
(значения даны в градусах)
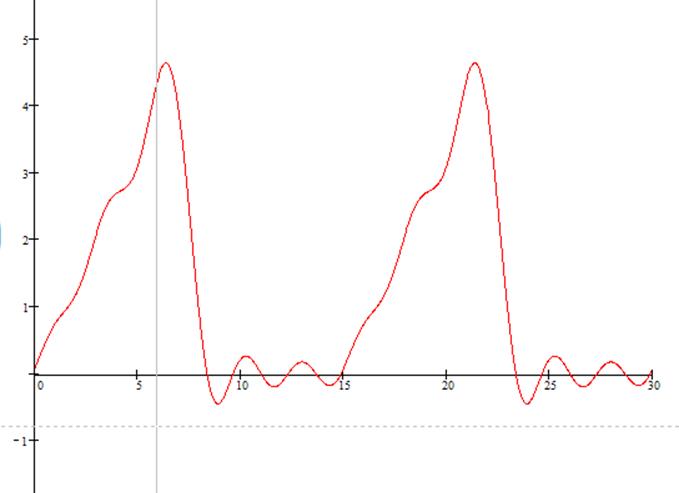
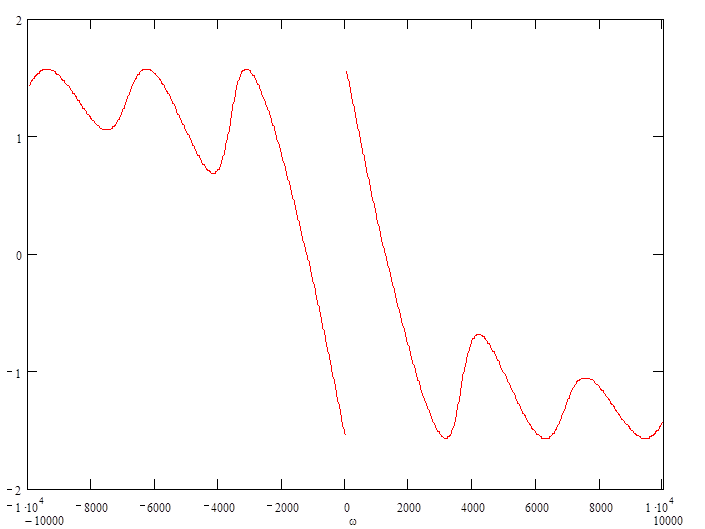
5. АЧХ и ФЧХ непериодического сигнала
Аналитически сигнал можно представить как :
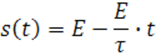
Спектральную плотность вычислим по формуле :
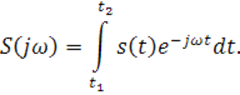
В нашем случае :
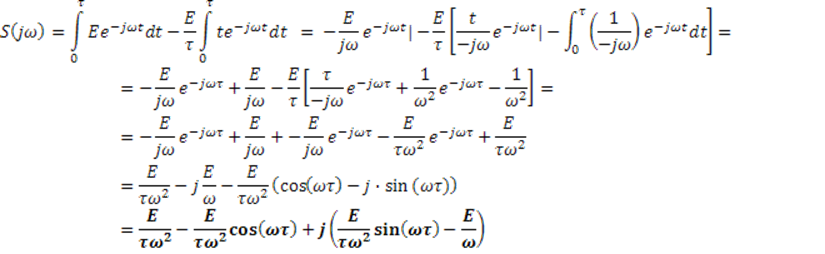
Подставив данные получим :
![]()
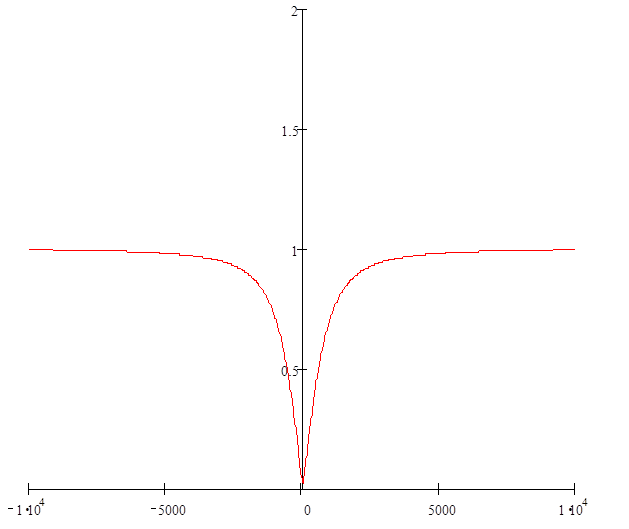
АЧХ сигнала :
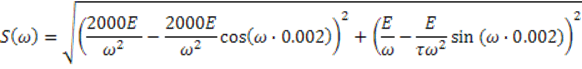
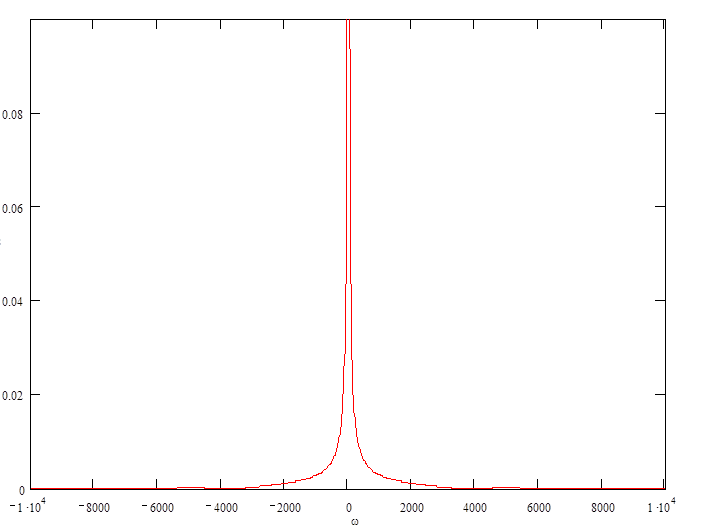
ФЧХ сигнала :
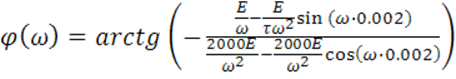
6.Отклик цепи на периодический сигнал
Выходной сигнал будет описываться следующим рядом :
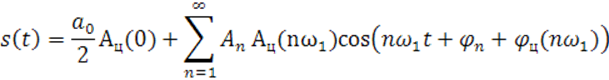
Где ![]() - это значение АЧХ цепи на данной
частоте , а
- это значение АЧХ цепи на данной
частоте , а ![]() – значение ФЧХ цепи на данной
частоте.
– значение ФЧХ цепи на данной
частоте.
Тогда сигнал на выходе можно будет описать так :
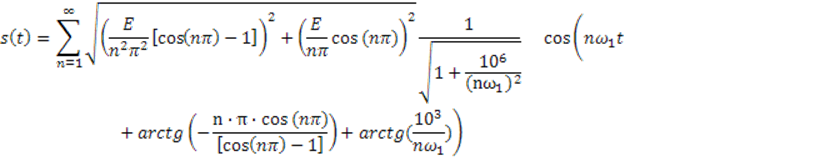
![]() :
:
|
гармоника |
частота |
АЧХ |
|
|
ФЧХ,° |
|
|
|
|
1570 |
0.843 |
0.377E |
0.318E |
32.49 |
-57.52 |
-25.03 |
|
|
3140 |
0.953 |
0.159E |
0.152E |
17.66 |
-90.00 |
-72.34 |
|
|
4710 |
0.978 |
0.107E |
0.104E |
11.99 |
-83.94 |
-71.95 |
|
|
6280 |
0.988 |
0.078E |
0.077E |
9.05 |
-90.00 |
-80.95 |
|
|
7854 |
0.992 |
0.064E |
0.063E |
7.26 |
-82.74 |
-75.48 |
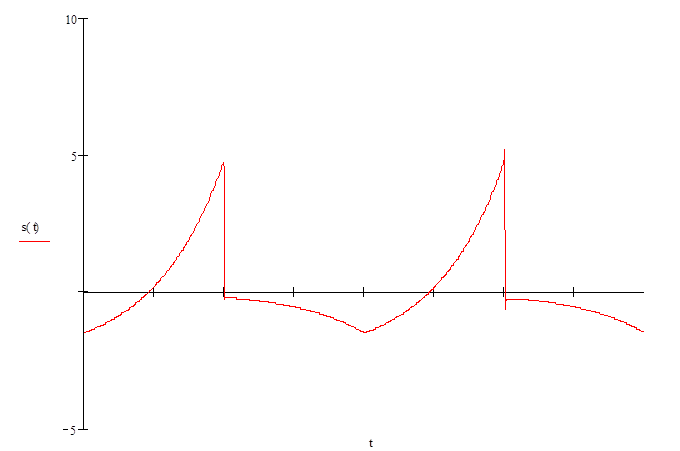
График построен для количества элементов n=500
6. Отклик цепи на непериодический сигнал


![]()
![]()
![]()
![]()

![]()
![]()
![]()
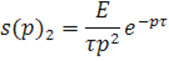
Представим наш сигнал как сумму двух других. Сигнал ![]() , изображение этой функции по
Лаплассу будет
, изображение этой функции по
Лаплассу будет ![]() , его легко найти , т.к. преобразование
Лапласса линейное , а изоброжения постоянной и прямой зависимости нам известны
. Сигнал
, его легко найти , т.к. преобразование
Лапласса линейное , а изоброжения постоянной и прямой зависимости нам известны
. Сигнал ![]() -E
,при
чём он должен начинаться в точке t=
-E
,при
чём он должен начинаться в точке t=![]() . изображение такой функции по
Лаплассу будет изображение обычной линейной зависимости , умноженное на
экспоненту
. изображение такой функции по
Лаплассу будет изображение обычной линейной зависимости , умноженное на
экспоненту ![]() , где
, где ![]() это время на которое сигнал
сдвинут во времени. Т.о.
это время на которое сигнал
сдвинут во времени. Т.о. ![]() .
.
Как видим из графиков , до момента времени ![]() существует только первая функция,
описывая наш входной сигнал , а с момента
существует только первая функция,
описывая наш входной сигнал , а с момента ![]() появляется вторая функция ,
которая является равной по модулю и противоположной по знаку , относительно
первой…таким образом , если сложить эти две функции , получится аналитическое
выражение , описывающее наш сигнал:
появляется вторая функция ,
которая является равной по модулю и противоположной по знаку , относительно
первой…таким образом , если сложить эти две функции , получится аналитическое
выражение , описывающее наш сигнал:
S(p)=![]() .
.
Реакцию цепи найдём с помощью обратного преобразования Лапласса от произведения спектральной плотности сигнала на коэффицент передачи цепи :
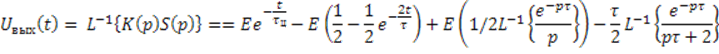
Как известно , ![]() - это единичный сигнал
существующий лишь в точке t=
- это единичный сигнал
существующий лишь в точке t=
![]()
А ![]() - это смещённая во времени
экспонента ,
- это смещённая во времени
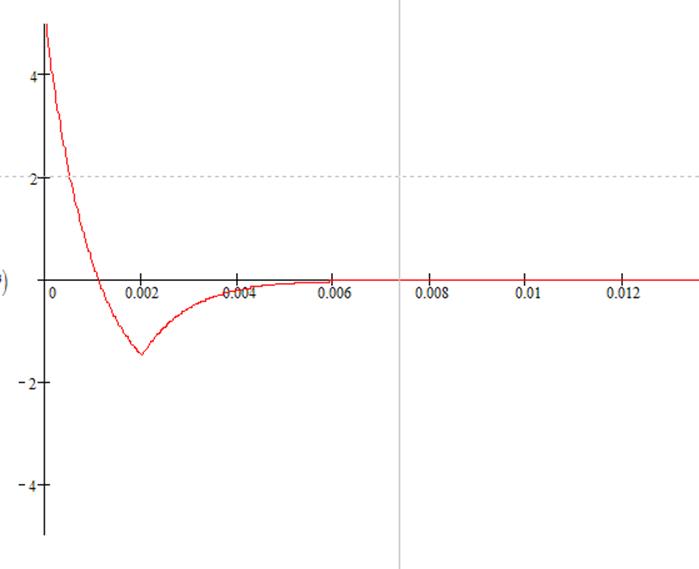
экспонента , ![]() . Таким образом суммарный выходной
сигнал будет иметь вид :
. Таким образом суммарный выходной
сигнал будет иметь вид :
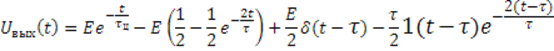
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.