



Министерство образования Российской Федерации
Владимирский государственный университет
Кафедра КТРЭС
Лабораторная работа №1
Работу выполнил:
Студент гр. РЭ-100
Работу проверил:
Владимир 2002
Цель работы: изучить методику планирования эксперимента, составить математическую модель узла РЭА и оптимизировать его параметры.
Теоретические сведения
Под планированием эксперимента понимают процесс определения числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью.
Уравнение регрессии задается полиномом вида: ![]() .
.
Коэффициент регрессии определяется формулой: 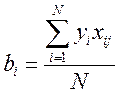 .
.
Вычисление коэффициентов регрессии проводится на основании ограниченного числа экспериментальных данных. Поэтому требуется проверить значимость полученных оценок, для чего служит критерий Стьюдента t:
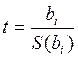 ,
,
Если рассчитанная величина критерия
превышает табулированное значение, то коэффициент ![]() признается
значимым. В противном случае коэффициент
признается
значимым. В противном случае коэффициент ![]() считается статистически незначимым. Член полинома с
этим коэффициентом можно исключить из уравнения полинома.
считается статистически незначимым. Член полинома с
этим коэффициентом можно исключить из уравнения полинома.
Проверка адекватности
осуществляется по критерию
Фишера: 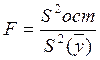 , . Уравнение считается адекватным
при соблюдении условия
, . Уравнение считается адекватным
при соблюдении условия ![]() , если записанное оно не
соблюдается, то модель признается неадекватной, и для математического описания
ТП необходимо подобрать полином более высокого порядка.
, если записанное оно не
соблюдается, то модель признается неадекватной, и для математического описания
ТП необходимо подобрать полином более высокого порядка.
Содержание работы
1. Разработать математическую модель электронного устройства с использованием активного факторного эксперимента.
2. Оптимизировать параметры элементов электронного устройства.
3. Экспериментально проверить результаты оптимизации на лабораторном макете.
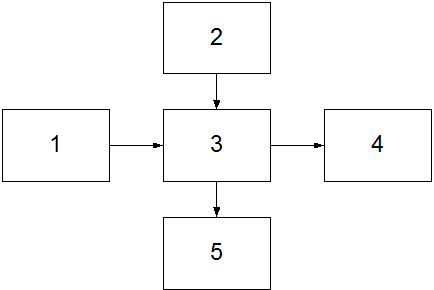
Структурная схема экспериментальной установки:
1. Генератор ГЗ-34
2. Источник питания БСП-50
3. Лабораторный макет УНЧ
4. Вольтметр ВЗ-6
5. Авометр АВО-5М1
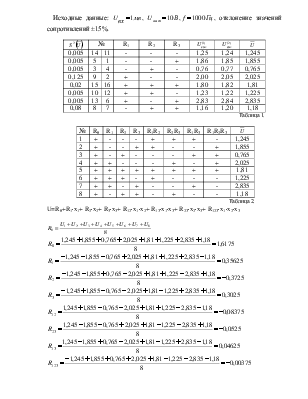
Исходные данные: ![]() ,
, ![]() ,
,![]() , отклонение значений
сопротивлений ±15%.
, отклонение значений
сопротивлений ±15%.
|
|
№ |
R1 |
R2 |
R3 |
|
|
|
|
|
0,005 |
14 |
11 |
- |
- |
- |
1,25 |
1,24 |
1,245 |
|
0,005 |
5 |
1 |
- |
- |
+ |
1,86 |
1,85 |
1,855 |
|
0,005 |
3 |
4 |
- |
+ |
- |
0,76 |
0,77 |
0,765 |
|
0,125 |
9 |
2 |
+ |
- |
- |
2,00 |
2,05 |
2,025 |
|
0,02 |
15 |
16 |
+ |
+ |
+ |
1,80 |
1,82 |
1,81 |
|
0,005 |
10 |
12 |
+ |
+ |
- |
1,23 |
1,22 |
1,225 |
|
0,005 |
13 |
6 |
+ |
- |
+ |
2,83 |
2,84 |
2,835 |
|
0,08 |
8 |
7 |
- |
+ |
+ |
1,16 |
1,20 |
1,18 |
Таблица 1.
|
№ |
R0 |
R1 |
R2 |
R3 |
R1R2 |
R2R3 |
R1R3 |
R1R2R3 |
|
|
1 |
+ |
- |
- |
- |
+ |
+ |
+ |
- |
1,245 |
|
2 |
+ |
- |
- |
+ |
+ |
- |
- |
+ |
1,855 |
|
3 |
+ |
- |
+ |
- |
- |
- |
+ |
+ |
0,765 |
|
4 |
+ |
+ |
- |
- |
- |
+ |
- |
+ |
2,025 |
|
5 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
1,81 |
|
6 |
+ |
+ |
+ |
- |
+ |
- |
- |
- |
1,225 |
|
7 |
+ |
+ |
- |
+ |
- |
- |
+ |
- |
2,835 |
|
8 |
+ |
- |
+ |
+ |
- |
+ |
- |
- |
1,18 |
Таблица 2.
U=R0+R1×x1+ R2×x2+ R3×x3+ R12×x1×x2+ R13×x1×x3+ R23×x2×x3+ R123×x1×x2×x3
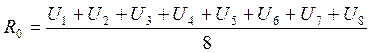
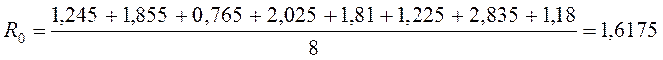
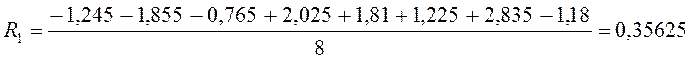
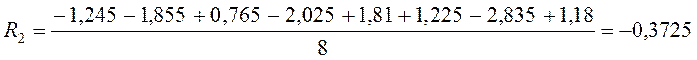
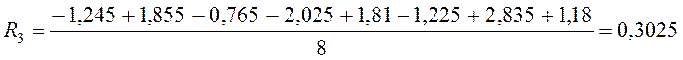
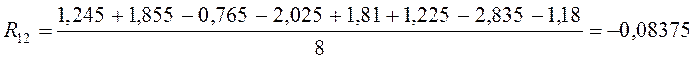
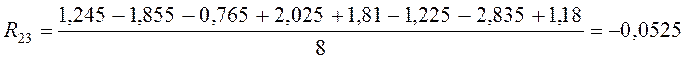
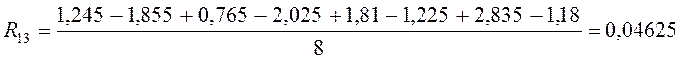
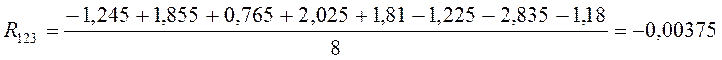
U=1,6175+0,35625×x1-0,3725×x2+0,3025×x3-0,08375×x1x2-0,0525×x2x3+0,04625×x1x3-0,00375×x1x2x3.
Проверка значимости коэффициентов регрессии.
Ошибка
эксперимента: 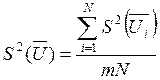 ,
, 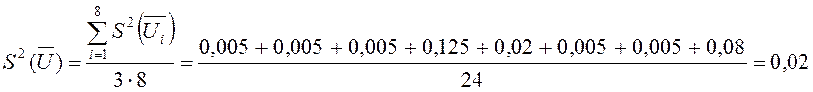 .
.
Дисперсия коэффициента
регрессии: 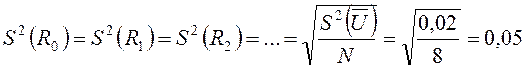 ;
; ![]() .
.
Для трёхфакторного эксперимента критерий Стьюдента t=2,37, тогда:
Коэффициент регрессии значим,
если: ![]() .
.
Значимость коэффициентов регрессии для:
R0: ![]()
R1: ![]()
R2: ![]()
R3: ![]()
R12: ![]()
R23: ![]()
R13: ![]()
R123: ![]() ,
,
коэффициент регрессии не значим, следовательно, его можно исключить из уравнения регрессии, поэтому оно принимает вид:
U=1,6175+0,35625×x1-0,3725×x2+0,3025×x3-0,08375×x1x2-0,0525×x2x3
Номер опыта |
Значения |
|
|
Экспериментальные (Uэ) |
Расчётные (Uр) |
|
|
1 |
1,245 |
1,24125 |
|
2 |
1,855 |
1,85875 |
|
3 |
0,765 |
0,76875 |
|
4 |
2,025 |
2,02875 |
|
5 |
1,81 |
1,81375 |
|
6 |
1,225 |
1,22125 |
|
7 |
2,835 |
2,83125 |
|
8 |
1,18 |
1,17625 |
Проверка адекватности:
Критерий
адекватности: выполнение условия ![]() .
.
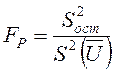 , где
, где ![]() - остаточная дисперсия:
- остаточная дисперсия:
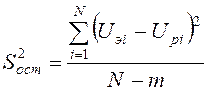 ,
,
Для трёхфакторного эксперимента при m=3, Fкр=3.
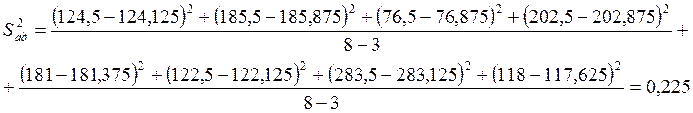
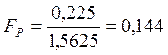 .
.
0,144<3, т.е. условие адекватности выполнено.
Вывод: В результате проведенной работы было составлено уравнение регрессии, и были найдены его коэффициенты. Значимость этих коэффициентов была проверена с помощью коэффициента Стьюдента, причем коэффициент R123 оказался, не значим, т.е. он особой роли в этом уравнении не играет, поэтому он был исключен из уравнения регрессии. Проверка адекватности показала, что данное уравнение адекватно, а значит выбранная степень уравнения регрессии достаточна. Таким образом, регрессионный анализ позволяет на основании небольшого количества экспериментальных данных получить математическую модель технологического процесса, необходимую для его исследования и управления, определения устойчивости его отдельных звеньев, для оценки качества готовой продукции и полуфабрикатов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.