Исследование законов распределения различных случайных процессов

Цель работы: исследование законов распределения различных случайных процессов – нормального шума, гармонического и  треугольного сигналов со случайными начальными фазами, суммы случайных взаимно независимых сигналов.

Теоретическая часть:

Случайный процесс – это изменение во времени физической величины (тока, напряжения и др.), значение которой невозможно заранее предсказать с вероятностью, равной единице.

Статистические свойства случайного процесса Х(t) можно определить, анализируя совокупность случайных функций времени , называемую ансамблем реализаций. Здесь k – номер реализации.

Статистические свойства случайного процесса характеризуются законами распределения, аналитическими выражениями которых являются функции распределения. Одномерная интегральная функция распределения вероятностей случайного процесса

где  - вероятность того, что мгновенное значение случайного процесса в момент времени t примет значение, меньшее или равное x.

Одномерная дифференциальная функция распределения случайного процесса, или плотность вероятности, определяется равенством

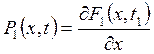
Одномерная плотность вероятности мгновенных значений суммы взаимно независимых случайных процессов  определяется формулой

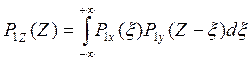, где - плотности вероятности процессов X(t),Y(t),Z(t).

Наиболее распространенными моментными функциями случайного процесса, определяемыми по одномерной плотности, являются:

- среднее значение (первый начальный момент)

;

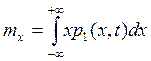- дисперсия (второй начальный момент)

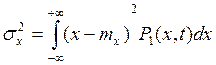
Для стационарных случайных процессов выполняются условия:

Статистические характеристики случайных процессов, имеющих эргодические свойства, можно найти также по времени одной реализации  продолжительностью T:

- среднее значение

;

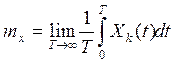- дисперсия

;

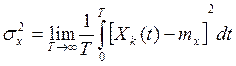- интегральная функция распределения

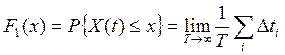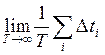, где  - относительное время пребывания реализации ниже уровня x;

- плотность вероятности

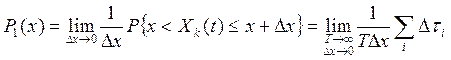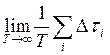, где - относительное время пребывания реализации в интервале  [].

Периодический сигнал со случайной фазой, равномерно распределенной  интервале от  до ,является стационарным эргодическим случайным процессом.

Для гармонического сигнала с амплитудой  и случайной начальной фазой , равномерно распределенной в интервале от до ,

плотность вероятности мгновенных значений

,  ;

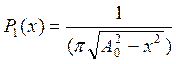дисперсия 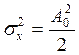;        математическое ожидание .

Для пилообразного сигнала, имеющего максимальное значение А и случайную равномерно распределенную фазу, плотность распределения вероятностей мгновенных значений

;

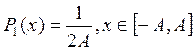дисперсия 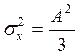; математическое ожидание равно нулю.

Плотность вероятности стационарного нормального шума с дисперсией  и математическим ожиданием

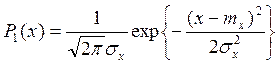
Структурная схема статистического анализатора, позволяющего экспериментально отыскивать дифференциальный закон распределения по точкам и наблюдать его на экране осциллографа: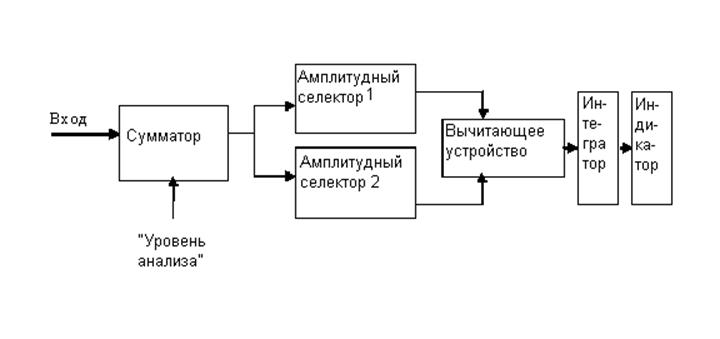

Сумматор и источник постоянного регулируемого напряжения позволяют использовать амплитудные селекторы с нерегулируемыми порогами срабатывания и обеспечивают возможность анализа сигналов различной полярности. На передней панели лабораторного статанализатора расположены клеммы «Вход», «Выход», «Уровень анализа».Требуемый уровень анализа подается от внешнего источника постоянного напряжения на клемму «Уровень анализа» и измеряется вольтметром. Порог амплитудного селектора первого канала выбирают нулевым; у амплитудного селектора второго канала порог селекции отличен от нуля на величину , называемую шириной канала анализа. С помощью амплитудных селекторов образуются прямоугольные импульсы, длительность которых равна времени пребывания входного сигнала ниже порогов срабатывания. Величина постоянной составляющей последовательности импульсов на выходе селектора первого канала пропорциональна ; на выходе селектора второго канала - , а на выходе вычитающего устройства

Выделение постоянной составляющей импульсов осуществляется интегратором и индикатором, функции которого при снятии закона распределения по точкам выполняет вольтметр постоянного тока.

Наблюдать законы распределения на экране осциллографа можно, если автоматически изменять уровень анализа синхронно с напряжением развертки осциллографа. Для этого можно использовать пилообразное напряжение развертки осциллографа, вход вертикального отклонения которого подключается к выходу статанализатора.

Практическая часть:  

Таблицы измерений

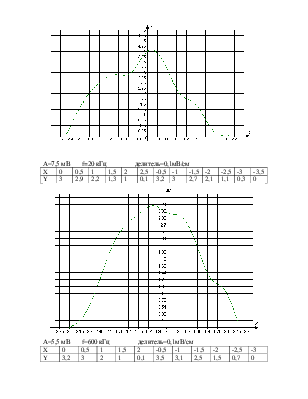
А=6,4 мВ      f=20 кГц                  делитель=50мВ/см

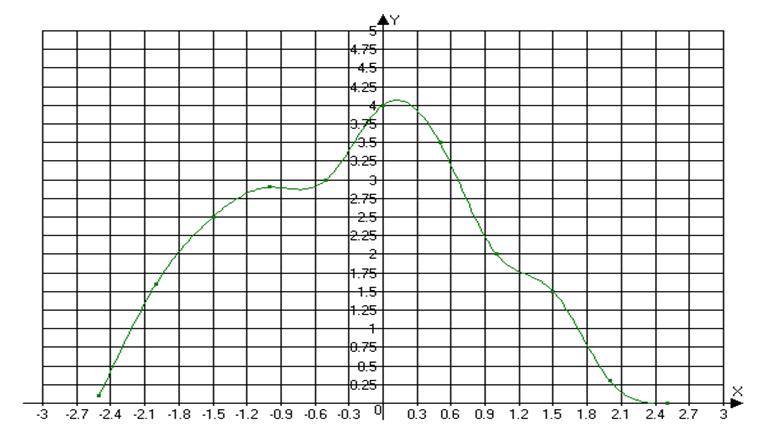
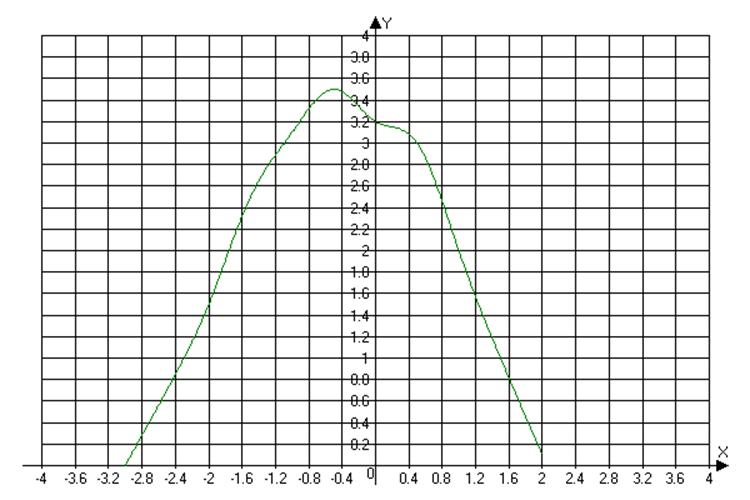
А=7,5 мВ       f=20 кГц                 делитель=0,1мВ/см

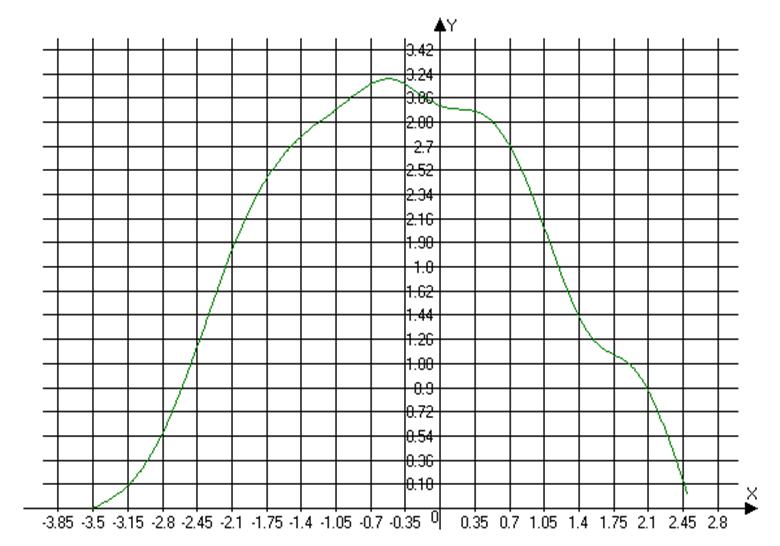
А=5,5 мВ       f=600 кГц                 делитель=0,1мВ/см

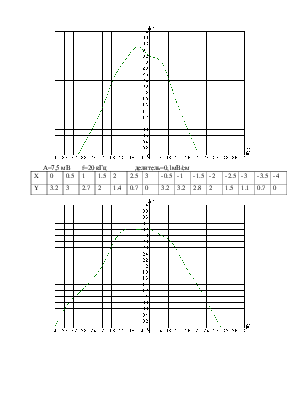
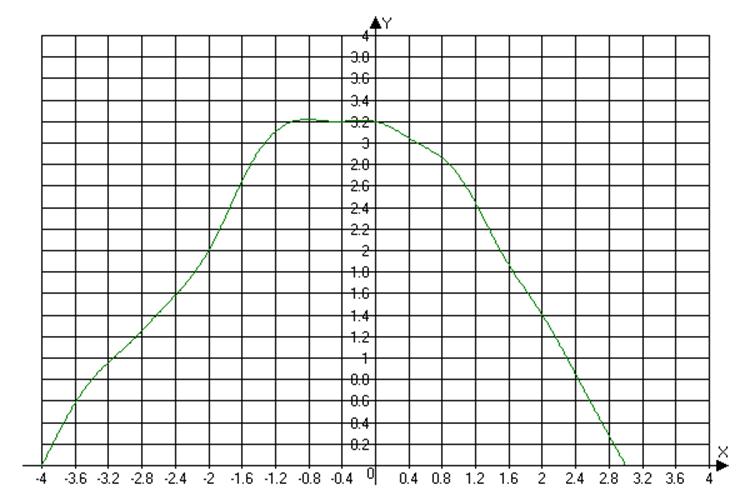
А=7,5 мВ       f=20 кГц                 делитель=0,1мВ/см