Принцип предельного поглощения и условия излучения на бесконечность

были рассмотрены при формулировании условия единственности решения внешних задач электродинамики (уравнений Максвелла).

10.2 Лемма Лоренца

Лемма Лоренца устанавливает взаимосвязь между интенсивностью сторонних источников, разнесенных в пространстве, и возбуждаемыми ими электромагнитными полями.

Предположим, что вблизи  точки 1 находится сторонний источник, который характеризуется , : , .

В точке 2 расположен другой источник , :, .Пусть среда характеризуется параметрами: 

Очевидно, что взаимосвязь между ними может быть описана уравнениями Максвелла:         

                                             

                                             

Аналогично для второго источника:

                                             

                                            

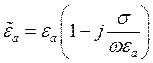
Умножим скалярно выражение на , выражение на , а затем вычтем из второго результата первый:

                                    

Умножим скалярно выражение на , а выражение на и из первого результата вычтем второй:

                                    

учтем следующие векторные тождества:

Используя и , можно записать следующим образом:

                                                

                                                

Из вычтем :

                                           

Уравнение называется леммой Лоренца в дифференциальной форме (соотношение справедливо в каждой точке пространства, где имеются сторонние источники).

Проинтегрируем по общему объему, который включает в себя все сторонние источники:

                       

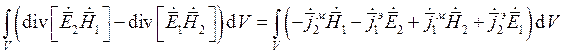
Левую часть преобразуем, используя теорему Остроградского-Гаусса. В соответствии с этой теоремой:

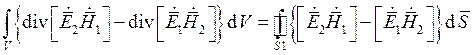                                       где S₁ — замкнутая поверхность, ограничивающая объем.

Тогда с учетом соотношение запишется в следующем виде:

                            

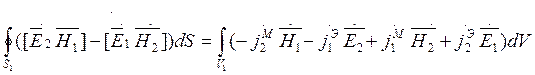
Выражение называется леммой Лоренца для ограниченного объема.

Рассмотрим случай бесконечного увеличения объема V₁. При этом поверхность S₁ размещается в бесконечно удаленных точках относительно расположения сторонних источников. В случае неограниченного объема V₁ поверхностный интеграл в равен 0. Это можно объяснить, используя 2 аргумента:

1)   поверхность S₁ удалена на бесконечность. Скорость распространения имеет конечное значение, то есть за любой конечный промежуток времени волны не смогут достигнуть поверхности S₁, иными словами, на поверхности S₁ отсутствуют составляющие поля, а, следовательно, интеграл по этой поверхности будет равен нулю

2)   как нам известно, в дальней зоне амплитуда составляющих поля убывает пропорционально 1/r. В случае реальных сред, которые характеризуются малыми, но конечными по величине потерями, амплитуда убывает еще быстрее. Таким образом, в реальных средах векторное произведение  в дальней зоне убывает быстрее, чем 1/r². Площадь сферы с ростом r возрастает пропорционально r². Таким образом, предел при :

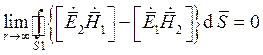
Таким образом, в случае неограниченного объема V₁ лемма Лоренца записывается в следующей форме:

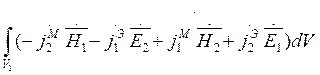=0    

10.3 Теорема взаимности для двух элементарных излучателей

Пусть в пространстве находятся 2 произвольно ориентированных излучателя. В точке 1 находится ЭЭИ, который характеризуется , . В точке 2 второй излучатель: ,

Обозначим  — напряженность электрического поля, возбуждаемого первым излучателем в месте расположения второго. И соответственно .

Применим лемму Лоренца для неограниченного объема:

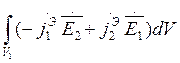=0                        

Интеграл в отличен от нуля только в точках пространства, где отлична от 0, т. е. в пределах объемов, занимаемых излучателями. Поэтому можно переписать следующим образом:

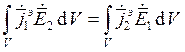
или

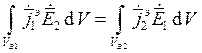,                         где V_В1 и V_В2 объемы, занимаемые первым и вторым излучателями (вибраторами). Ввиду малости излучателей () можно считать, что,

Из данных  выводов следует:

                      

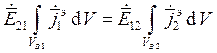
Элементы объема dV можно записать следующим образом 

1:    

2:   

где  и  – площадь поперечного сечения первого и второго излучателей.

Учитывая, что d ЭЭИ << длины можно предполагать, что амплитуда векторов объемной плотности электрического тока в пределах поперечного сечения неизменна. Применим эти условия для соотношения (3).

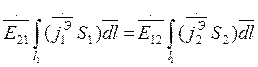
В силу малости ЭЭИ амплитуду тока можно считать неизменной. Поэтому ее можно вынести за знак интеграла:

                            

                                    

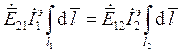
Теорема взаимности ЭЭИ позволяет определить одну из величин, входящих в уравнение .

Теорема взаимности может быть получена и для ЭМИ. Используя лемму Лоренца и аналогичные преобразования, легко можно получить:

                                  

Используя лемму Лоренца, можно получить выражение для теоремы