Использование избыточности при некоррелированных мешающих воздействиях, страница 4

Пусть он равен S_вых(t)= A_b(t)cos[ω₀t+φ_b(t)+φ₀], где в изменениях амплитуды А_b(t) и фазы φ_b(t) заключена передаваемая информация, а φ₀ - некоторая начальная фаза и центральная частота.

Входные разнесенные сигналы имеют вид: S_i=K_iA_b(t)cos[ω₀t+φ_b(t)+φ_i], где K_i и φ _i- коэффициент передачи в данную ветвь разнесения  и фазовый сдвиг в ней.

После ограничителя амплитуды (ОГР) и фазовращателя (на 90⁰) сигналы имеют вид U₀cos[ω₀t+φ_b(t)+φ₀] и U₀sin[ω₀t+φ_b(t)+ φ₀].

После перемножения в перемножителях (´) и фильтрации в ФНЧ в однотипных блоках каждой ветви разнесения получаются весовые коэффициенты при ортогональных компонентах, пропорциональные

a_ic~K_icos(φ_i-φ₀),    a_is~K_isin(φ_i-φ₀).

В регулируемых усилителях (РУ) производится регулировка величины сигнала в соответствии с этими коэффициентами. При этом сумма двух получаемых ортогональных компонентов

S_ic(t)+S_is(t)=a_ciK_iA_bcos[ω₀t+φ_b(t)+φ_i]+a_siK_iA_bsin[ω₀t+φ_b(t)+φ_i]=                                  

=A_bK_i²cos[ω₀t+φ(t)+φ₀].

Таким образом, кроме фазирования разнесенные сигналы одновременно складываются пропорционально квадратам их уровней, что при одинаковых уровнях шума в каналах близко к оптимальному сложению.

В случае частых глубоких замираний вероятны провалы выходного сигнала ниже уровня ограничения, что ведет к срыву фазовой подстройки. При этом может быть использована схема с управляемым генератором (УГ) и цепью фазовой автоподстройки (ФАП) (на рис. 28.4 это показано пунктиром). Напряжение опорного генератора непрерывно сравнивается с выходным сигналом и подстраивается под него. В моменты, когда уровень выходного сигнала падает, амплитуда сигнала управляемого генератора остается постоянной.

В некоторых ситуациях для фазирования можно использовать другие операции, которые проводятся при демодуляции, например для понижения порога при частотной модуляции путем уменьшения ее индекса. Сходные принципы применяются в «следящих гетеродинах».

С целью фазирования складываемых сигналов можно применить другие методы, например метод понижения полрога детектирования при частотной модуляции. На рис. 28.5 для этой цели использован преобразователь частоты.

Рис. 5

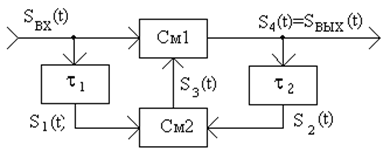Входной частотно-модулированный сигнал равен  S_вх(t)=A_вхcos[ω₀t+φ_вх(t)],  где передаваемая информация заложена в изменениях фазы  φ_вх(t).

После прохождения линии задержки с временем задержки τ₁ получается сигнал S₁(t)= S_вх(t-τ₁)= A₀cos[ω₀t-ω₀ τ₁+ φ_вх(t-τ₁)]. На выходе схемы присутствует сигнал S_вых=A_выхcos[ω₁t+ψ(t)], где ψ(t) - фаза, меняющаяся по некоторому закону, вид которого можно найти следующим образом.

После прохождения через вторую линию задержки с некоторой задержкой τ₂ сигнал будет иметь вид

S₂(t)=S_вых(t-τ₂)= A₂cos[ω₂t-ω₂τ₂+ψ(t-τ₂)].

Величина задержки выбирается кратной периоду соответствующих частот, т.е. τ₁₌2πn/ω₀; τ₂₌2πm/ω₁, где m и n – целые числа. При этом

S₁(t)= A₁cos[ω₀t+ φ_вх(t-τ₁)],       S₂(t)= A₂cos[ω₁t+ψ(t-τ₂)].

Фильтр смесителя См2 выделяет суммарную частоту двух перемножаемых сигналов S₃(t)=A₃cos[(ω₀+ ω₁)t+φ_вх(t-τ₁)+ψ(t-τ₂)].

Фильтр смесителя См 1 выделяет сигнал разностной частоты передаваемых сигналов. На его выходе сигнал равен

S₄(t)=A₄cos{[(ω₀+ω₁)t+φ_вх(t--τ₁)+ψ(t-τ₂)]-[ω₀t+φ_вх(t)]}=

= A₄cos{ω₁t+[φ_вх(t-τ₁)-φ_вх(t)]+ψ(t-τ₂)}.

Но S₄(t)=S_вх(t)  и после приравнивания аргументов косинусов получим  φ_вх(t-τ₁)-φ_вх(t)+ψ(t-τ₂)=ψ(t).

Величины времени в обеих задержках выбираются много меньше периода максимальной частоты модулирующего сигнала. В этом случае справедливы приближенные равенства:

φ_вх(t-τ₁)-φ_вх(t)≈-τ₁dφ_вх(t) ∕ dt;             ψ(t)-ψ(t-τ₂)≈τ₂dψ(t) ∕ dt.

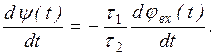Отсюда

Но полученные производные от мгновенной фазы равны мгновенным частотам входного и выходного сигналов. Меняя соотношение между временами задержки можно изменять девиацию ЧМ сигнала на выходе схемы.

Путем незначительной модификации схему можно использовать одновременно и для фазирования разнесенных сигналов. Вариант модификации приведен на рис. 28.6.

В каждой ветви присутствуют одинаковые блоки, состоящие из смесителей (См 1 и См 2), настроенных, соответственно, на разностную и суммарную частоты, и линии задержки τ₁, величина временной задержки в которой много меньше T_b, где T_b- период верхней частоты модулирующего сигнала.

В точках 4 всех ветвей разнесения сигналы будут практически синфазны, и сложение в сумматоре можно производить любым методом.  Мгновенное изменение частоты выходного сигнала будет равно  ψ(t)=-(τ₁∕τ₂)φ(t), т.е. при этом одновременно будет уменьшен в необходимое число раз индекс модуляции.

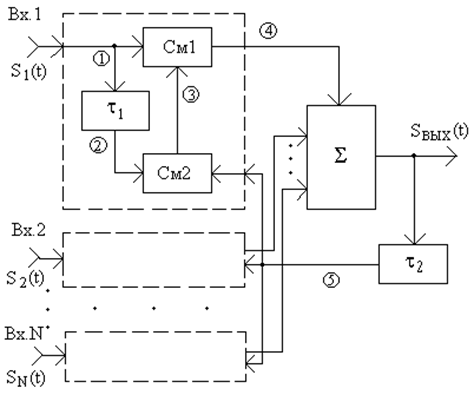Рис. 28.6.