Использование избыточности при некоррелированных мешающих воздействиях, страница 3

Если же уровни полезных сигналов группируются около некоторого среднего, отклонения от которого выражены в меньшей степени, (например, при рэлеевском распределении), то совместное распределение Х₁ и Х₂ больше тяготеет к биссектрисе прямого угла (обозначено кружками). Здесь линейное сложение имеет преимущества перед автовыбором.

Подобная простейшая ситуация без труда распространяется на большую кратность разнесения. В частности, при N-кратном разнесении  координаты, соответствующие сигналам Х_1,…, Х_N, образует N-мерную прямоугольную систему.  В этом случае оптимальному сложению соответствует часть N-мерной гиперсферы.

Автовыбору соответствует N-мерный гиперкуб, гранями прилегающий к многомерным координатным плоскостям. Линейному сложению соответствует грань N-мерного гипермногогранника, касающаяся гиперсферы в точке пересечения ее поверхности биссектрисой N-мерного угла из начала координат.

Гиперсфера также вписана одновременно и в гиперкуб, и в гипермногогранник. Многомерное распределение величин Х₁,…,Х_N также, в зависимости от его вида, тяготеет либо к координатным плоскостям, либо к биссектрисе многомерного угла, поэтому вывод о взаимных преимуществах автовыбора и линейного сложения в зависимости от глубины замираний остается в силе.

Это графическое представление можно использовать для рассмотрения ситуаций, когда необходимые значения весовых коэффициентов не удается измерить с требуемой точностью (рис. 28.2).

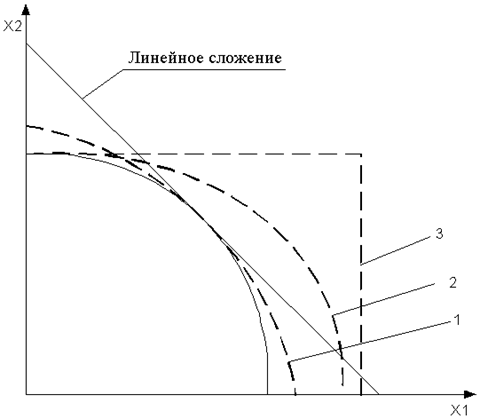Рис. 28.2.

Пусть, как и рассматривалось ранее, измеряются не требуемые величины  |А₁| и |А₂| , а искаженные ошибкой из-за присутствия шума, т.е. α₁=. и, α₂=,(величины σ²_M1  и σ²_M2  положим одинаковыми и равными σ²_M).

Пусть в некоторой ситуации величины полезных сигналов |А₁|, |А₂| >> σ_M², α₁=|А₁|, α₂=|А₂|. В этом случае действительно реализуется  сложение, близкое к оптимальному.

Теперь пусть в другой ситуации |А₁|, |А₂| << σ_M², тогда α₁≈ σ_M, α₂≈ σ_M, т.е. α₁≈ α₂  и сложение вместо оптимального близко к линейному.

Промежуточная ситуация соответствует промежуточному положению (кривая 1 на рис. 2). Если σ²_M1 ≠ σ2_M2, то кривая  будет находиться также между жирными линиями, но станет несимметричной.

Ситуация, когда мощности шума в каналах  неодинаковы и определены неверно, соответствует кривым 2 (для оптимального сложения) и 3 (для автовыбора) и приводит к деформации соответствующих диаграмм.

Поскольку при линейном сложении величины s_Мi не учитываются, то диаграмма для этого метода не меняется.

Таким образом, при неверной оценке уровней шума в ветвях разнесения, выводы о сравнительной помехоустойчивости методов комбинирования необходимо пересмотреть в сторону преимуществ линейного сложения. В частности, становится возможными ситуации, когда сложение сигналов по методу, ранее бывшему оптимальным, (т.е. обеспечивавшим максимальное отношение сигнал/шум), может проигрывать линейному сложению. Условия для этого в виде конкретных видов многомерных распределений сигналов вполне находят себе место в реальности в рамках четырехпараметрической модели замираний.

          При фазировании складываемых сигналов их сдвиги фаз сравниваются с фазой некоторого опорного сигнала (при частотном разнесении сигналы предварительно переносятся на одну несущую частоту). В соответствие с результатом сравнения производится регулировка сдвига фаз до совпадения с фазой опорного. В качестве опорного сигнала может быть использован либо сигнал независимого местного генератора, либо сигнал, формируемый с помощью входных разнесенных сигналов (рис. 28.3).

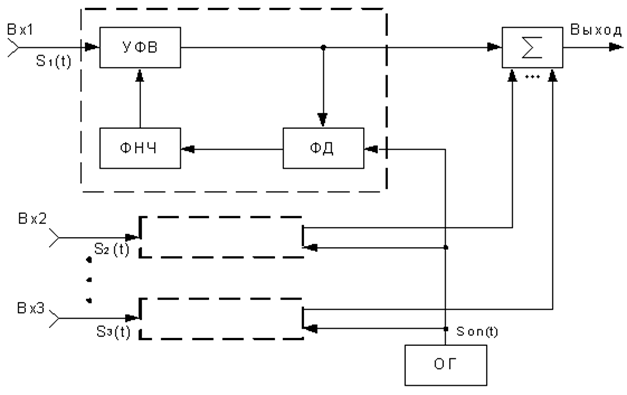Рис. 28.3

При этом в однотипных блоках производится сравнение фазы сигнала S_оп(t) с опорного генератора  (ОГ) в фазовых детекторах (ФД), далее результат фиксируется в ФНЧ и управляет перестройкой фазы в управляемых фазовращателях (УФВ).

Полоса ФНЧ выбирается таким образом, чтобы отфильтровать сигнал, пропорциональный разности ОГ и входного сигнала в этой ветви ∆φ=arg{S_ОП(t)-S_i(t)}, соответствующий случайному фазовому сдвигу.

Это возможно, если спектры информационного сигнала и случайного фазового сдвига не совпадают. Например, в тропосферном или КВ каналах они обусловлены быстрыми замираниями и нестабильностью частот генераторов. Если же спектры перекрываются, то происходит либо неполное фазирование, либо потеря части информации.

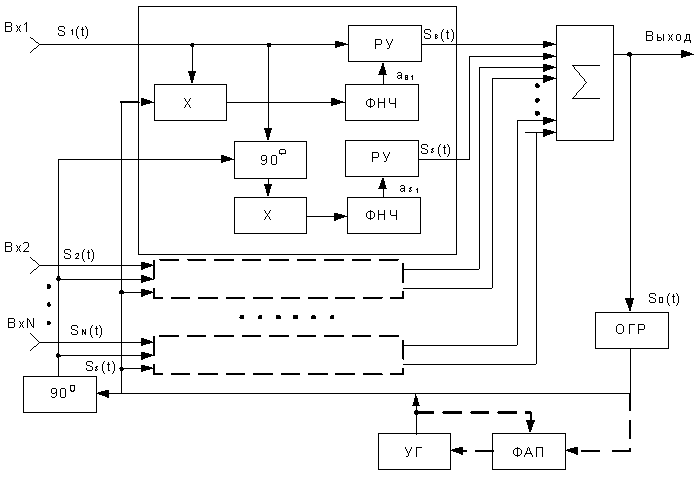В схеме на рис. 28.4 для создания опорного сигнала используется выходной информационный сигнал.

Рис. 28.4