Влияние мешающих воздействий на избыточность сигналов, страница 2

Более сложная картина наблюдается, когда величины спектральных составляющих помехи на различных частотах как-либо зависимы между собой. Например, в амплитудно модулированной шумовой помехе величины спектральных составляющих, расположенных симметрично относительно несущей, одинаковы.

Аналогично первоначальному рассмотрению разобьем всю полосу F спектра на n одинаковых полос . Компоненты помехи , попадающие в эти полосы, образуют некоторый ансамбль {y_i} и имеют многомерную плотность распределения , энтропия которой равна Н_ny. Когда процессы y_i-независимы, то

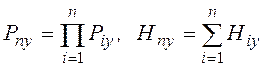, где Р_iy и Н_iy - распределения и энтропии соответствующих процессов.

Если же между какими-либо у_i имеется любая зависимость, то Р_nyуже не является произведением вероятностей Р_iy, которые из безусловных становятся условными. Выражение для Р_ny усложняется, однако качество связи принято определять по энергетическим параметрам, поэтому взаимосвязь между y_i будет рассматриваться в рамках взаимно-корреляционных связей.

Пусть  - вектор-столбец, составленный из элементов у_i. Тогда взаимно-корреляционная матрица В процессов у_i равна , где значок «Т» и черта над формулой означают, соответственно, операции транспонирования и усреднения по времени. В случае отсутствия корреляционных зависимостей между процессами у_i матрица В - диагональная, элементы главной диагонали пропорциональны средним мощностям  процессов. С появлением корреляционных связей появляются  ненулевые элементы и вне главной диагонали.

Обозначим  где S_i - части полезного сигнала, попадающие в полосы , и образуем вектор , состоящий из таких элементов. Тогда, как известно, максимальное общее отношение сигнал/помеха достигалось бы, если все компоненты были объединены (при соответствующем фазировании) с некоторыми коэффициентами , определяемыми по формуле Винера-Хопфа

где вектор  составлен из элементов . При этом достигается максимально возможное отношение сигнал/шум, равное

В общем случае можно считать все области спектра полезного сигнала  равноправными, содержащими парциальные компоненты одинаковой мощности:

.

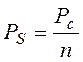Тогда все элементы вектора  одинаковы

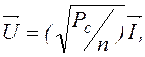
где -  единичный вектор (все n его элементов равны единице).

При этом

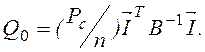
Естественно, здесь величина Q₀ другая, чем в ситуации, когда все спектральные компоненты независимы. Подобное максимальное отношение сигнал/помеха и характеризует избыточность по уровню (как компонент выражения для объема сигнала) при сравнении с исходным сообщением.

Распространяя подход, применяемый к рассмотренному дискретному

В случае разнесенного приема воздействие помех также снижает избыточность сигнала. Эффективность разнесения, как средства борьбы с замираниями сигнала, пропорциональна кратности разнесения при отсутствии внешних помех. В случае воздействия помех большого уровня, меры, устраняющие их воздействие, одновременно приводят к изменению соотношений в ансамбле полезных сигналов.

Это проявляется в том, что соотношения в новом ансамбле соответствуют (в смысле борьбы с замираниями) ситуации меньшей кратности разнесения, чем физически имеющая место в реальности. При этом уменьшается и избыточность.