Дискретная фильтрация в системе Matlab. Изучение возможностей MATLAB для фильтрации сигналов

Лабораторная работа

Дискретная фильтрация в системе Matlab

Цель работы.Изучение возможностей MATLAB для фильтрации сигналов.

Задание 1. Изучить материал, изложенный ниже, и повторить примеры и упражнения, приведенные в тексте.

Функции, используемые для расчета частотной характеристики фильтра и результатов фильтрации

Основной характеристикой дискретного фильтра является функция передачи или системная функция

H(z)= (b₀+b₁*z^-2+….b_m*z^-m) / ( 1 + a₁*z^-1 +a₂*z^-2+...a_n*z^-n). Для расчета частотной характеристики фильтра используется функция freqz. Пример построения амплитудно-частотной характеристики (АЧХ):

b=[1 2 3 4];

a=[1 0.1];

N=1024;

Fs=1e6;

[h,f] = freqz(b,a,N,Fs);

plot(f,abs(h));

Здесь векторы: b, a – наборы коэффициентов числителя и знаменателя системной функции, соответственно; N – число точек расчета (по умолчанию – 512); Fs – частота дискретизации. Выходные параметры: h, f - комплексный коэффициент передачи и вектор частот, для которых проведен расчет. Для построения фазочастотной характеристики (ФЧХ) используется функция phasez. Пример:

[phi,f] = phasez(b,a,N,Fs);

plot(f,phi);

Если использовать функцию freqz без указания выходных параметров, то строятся графики АЧХ и ФЧХ. Пример: freqz(b,a,N,Fs);

Для расчета результатов фильтрации используется функцияfilter(b,a,x). Здесь x – вектор входного сигнала. Синтаксис вызова функции следующий: y= filter(b,a,x). Здесь y– вектор выходного сигнала. Пример:

Fs=1000;

t=0:1/Fs:1;

f1=10;

f2=100;

s1=sin(2*pi*f1*t);

s2=sin(2*pi*f2*t);

s=s1+s2;

plot(t,s);

B=fir1(150,0.02, 'low');

freqz(B,1,[],Fs)

y=filter(B,1,s);

plot(t,y);

В данном примере использована функция fir1(N,Wn,'low') расчета нерекурсивного фильтра нижних частот. Здесь N – порядок фильтра, Wn - частота среза (на уровне -6дБ), нормированная к половине частоты дискретизации (в данном примере Wn=0,02*0,5*1000=10Гц). Если последний параметр функции принимает значения: 'high', 'bandpass', 'stop', то имеют место, соответственно, фильтр верхних частот, полосовой фильтр, режекторный фильтр. В последних двух случаях параметр Wn = [W1 W2], где W1, W2 – граничные частоты.

Функция filterможет также использовать параметры фильтра, если последний задан в виде объекта. Синтаксис вызова функции в этом случае следующий: y1 = filter(Hd,x). Здесь Hd – объект дискретного фильтра. Для создания объекта дискретного фильтра служит функция dfilt. Пример вызова функции:

Hd = dfilt.dffir(b)

После точки указывается идентификатор структуры фильтра (в данном примере используется структура прямой формы нерекурсивного фильтра), в скобках указываются параметры структуры (в данном случае - вектор коэффициентов фильтра). Для данных предыдущего примера использование фильтра в форме объекта показано нижеследующим примером.

Hd = dfilt.dffir(B);

y1 = filter(Hd,s);

plot(t,y1);

Проектирование фильтров

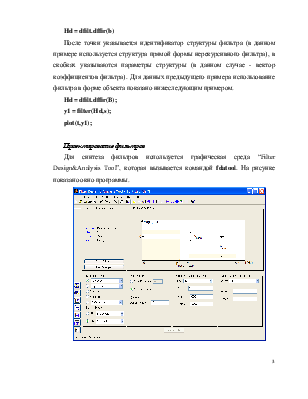
Для синтеза фильтров используется графическая среда “Filter Design&Analysis Tool”, которая вызывается командой fdatool. На рисунке показано окно программы.

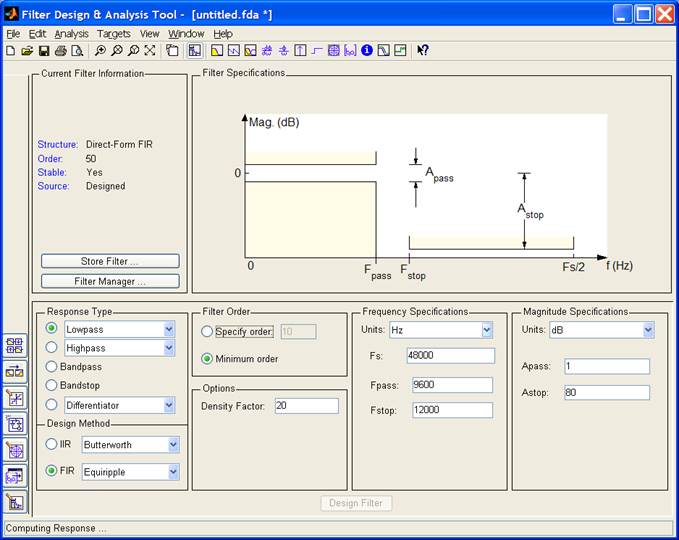
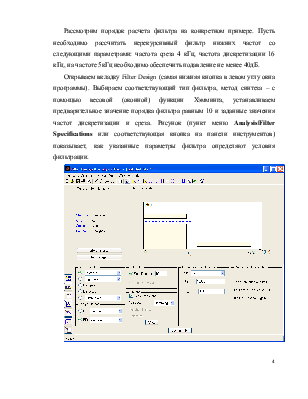
Рассмотрим порядок расчета фильтра на конкретном примере. Пусть необходимо рассчитать нерекурсивный фильтр нижних частот со следующими параметрами: частота среза 4 кГц, частота дискретизации 16 кГц, на частоте 5кГц необходимо обеспечить подавление не менее 40дБ.

Открываем вкладку Filter Design (самая нижняя кнопка в левом углу окна программы). Выбираем соответствующий тип фильтра, метод синтеза – с помощью весовой (оконной) функции Хэмминга, устанавливаем предварительное значение порядка фильтра равным 10 и заданные значения частот дискретизации и среза. Рисунок (пункт меню Analysis|FilterSpecifications или соответствующая кнопка на панели инструментов) показывает, как указанные параметры фильтра определяют условия фильтрации.

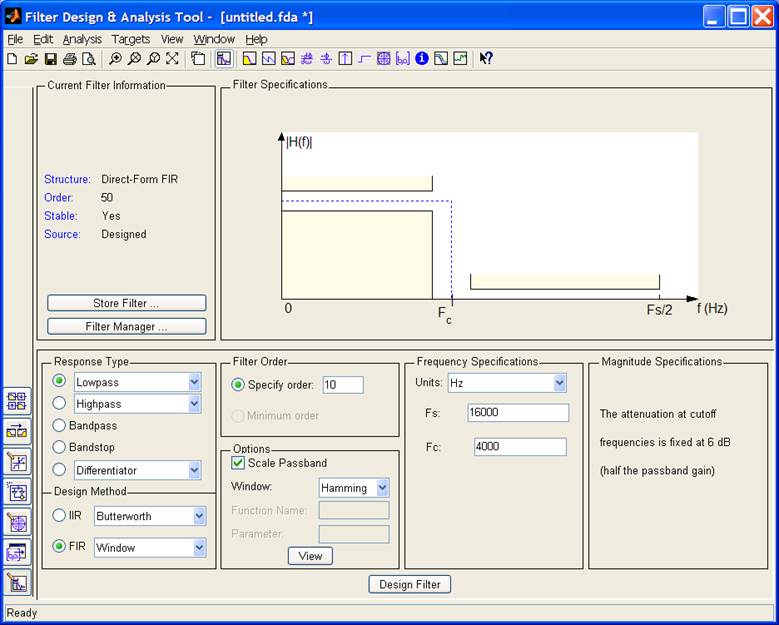
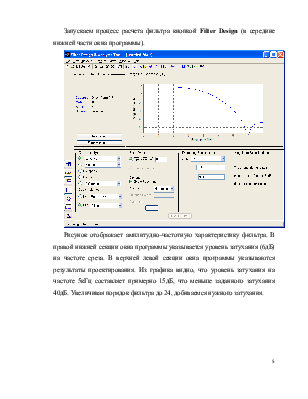
Запускаем процесс расчета фильтра кнопкой FilterDesign (в середине нижней части окна программы).

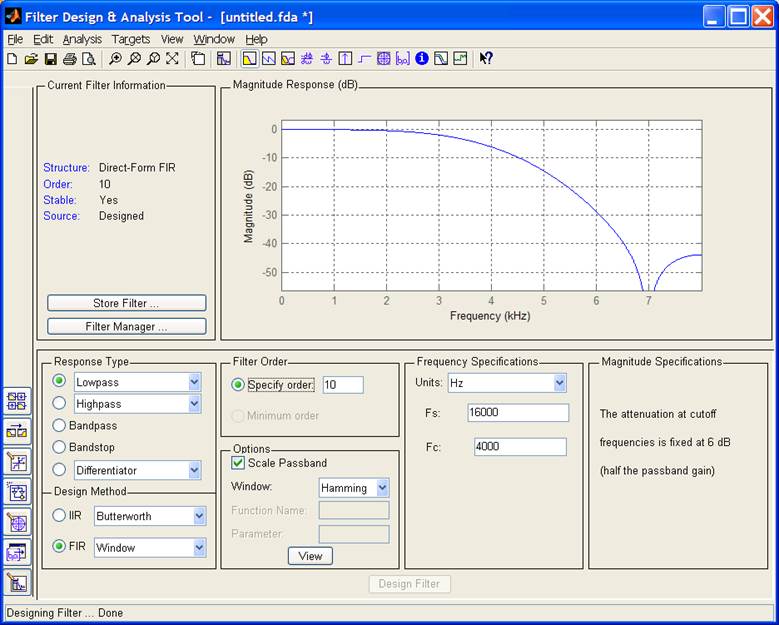
Рисунок отображает амплитудно-частотную характеристику фильтра. В правой нижней секции окна программы указывается уровень затухания (6дБ) на частоте среза. В верхней левой секции окна программы указываются результаты проектирования. Из графика видно, что уровень затухания на частоте 5кГц составляет примерно 15дБ, что меньше заданного затухания 40дБ. Увеличивая порядок фильтра до 24, добиваемся нужного затухания.

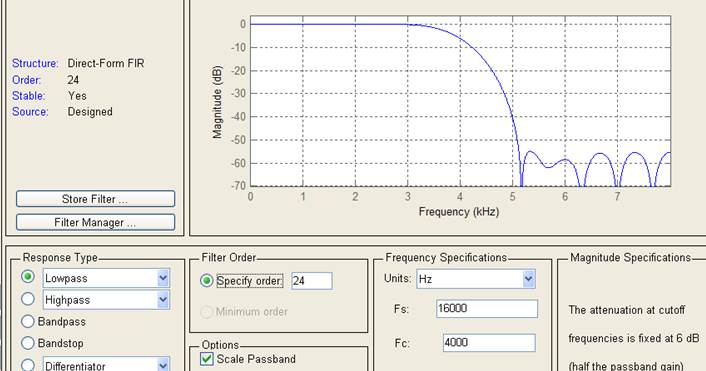
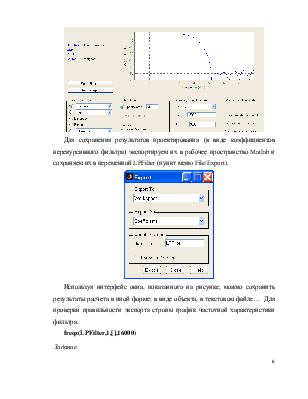
Для сохранения результатов проектирования (в виде коэффициентов нерекурсивного фильтра) экспортируем их в рабочее пространство Matlab и сохраняем их в переменной LPFilter (пункт меню File|Export).

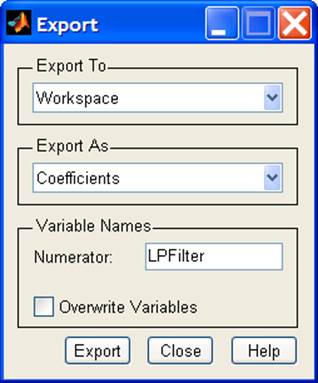
Используя интерфейс окна, показанного на рисунке, можно сохранить результаты расчета в иной форме: в виде объекта, в текстовом файле…  Для проверки правильности экспорта строим график частотной характеристики фильтра.

freqz(LPFilter,1,[],16000)

Задание

1. Повторить все приведенные выше примеры

2. Сформировать массив звуковых данных, пораженных гармонической помехой, используя заданный звуковой файл.

3.Провести спектральный анализ полученного массива заданным методом. Сформулировать необходимые требования к фильтру, устраняющему помеху.

4.Спроектировать соответствующий нерекурсивный фильтр, используя метод весовых функций.

5. Отфильтровать пораженный помехой звуковой сигнал и оценить результаты фильтрации.

6. Построить таблицу изученных команд и функций с пояснениями по их использованию

Содержание отчета

1.  Распечатка истории команд.

2.  Графики по итогам выполнения задания.

3.  Таблица изученных команд и функций с пояснениями по их использованию

Контрольные вопросы

1.Ответить на вопросы по использованию изученных команд и функций

2. Ответить на вопросы по использованию графической среды проектирования фильтров.