Формирование и анализ сигналов в системе MATLAB

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального

образования

Владимирский государственный университет

Кафедра РТ РС

Лабораторная работа №4

Формирование и анализ сигналов в системе MATLAB

                                                                                       Выполнил ст. гр. РТм-110

                                                             

                                                                                Проверил:

Владимир 2010

Цель работы.Изучение основных функций MATLAB для анализа сигналов.

I. Тексты решений задач и графики по итогам решения.

Односторонний экспоненциальный импульс:

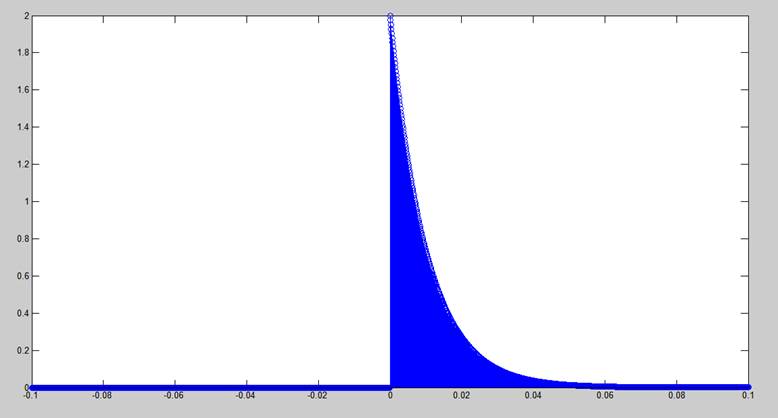
Fs = 8e3;

t = 0:1/Fs:1;

t = t';

alpha = 0.1e3;

A = 2;

t = -0.1:1/Fs:0.1;

s = A * exp(-alpha * t) .* (t >= 0);

stem(t,s)

Прямоугольный импульс, центрированный относительно начала отсчета времени:

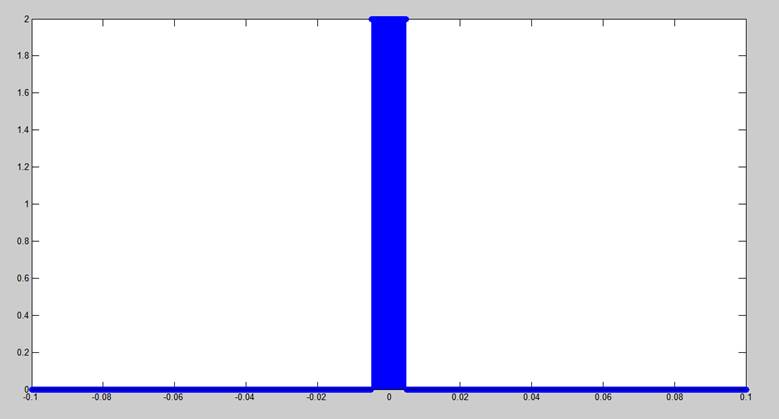
T= 0.01;

t = -0.1:1/Fs:0.1

s = A * (abs(t) <= T/2);

stem(t,s)

Пример формирования несимметричного треугольного импульса:

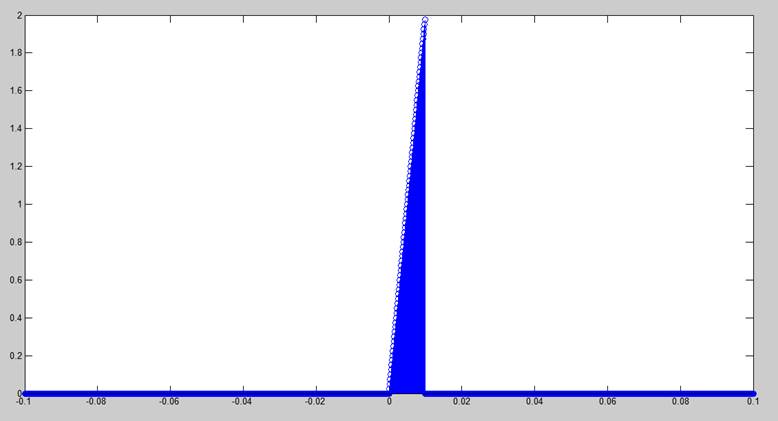
s = A * t / T .* (t >= 0) .* (t <= T);

stem(t,s)

Сформируем пару разнополярных прямоугольных импульсов с амплитудой 5В и длительностью 20мс каждый, расположенных справа и слева от начала отсчета времени. Частоту дискретизации выберем равной 1 кГц.

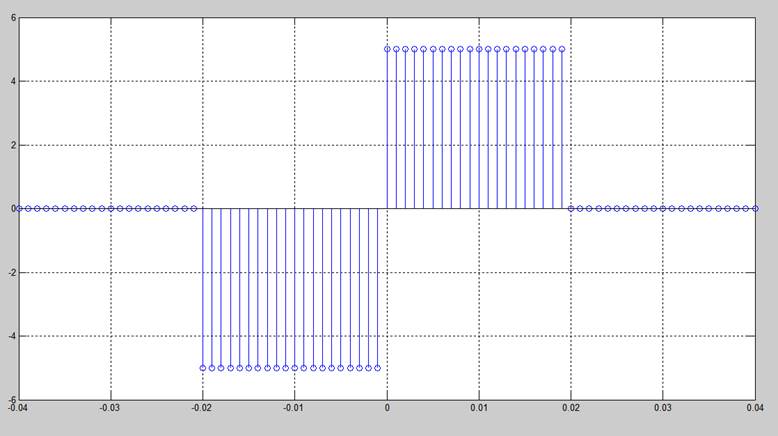
Fs = 1e3;

t = - 40e-3 :1/Fs: 40e-3;

Т = 20е-3;

T= 20e-3;

A = 5;

s = - A * rectpuls(t+T/2, T) + A * rectpuls(t-T/2, T);

stem(t, s);

ylim([-6 6])

grid on

Сформируем последовательность однополярных прямоугольных импульсов с амплитудой 2В, частотой следования 50Гц и длительностью 5мс. Частота дискретизации 10 кГц и временной интервал -10... 50 мс:

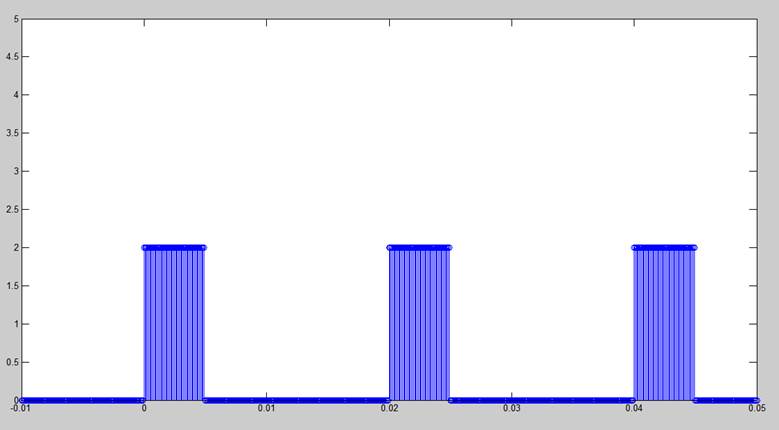
Fs = 1e4;

t = -10e-3:1/Fs:50e-3;

A = 2;

f0 = 50;

tau = 5e-3;

s = (square(2*pi*t*f0, f0*tau*100) + 1) * A/2;

stem(t, s);

ylim([0 5]);

1.  Сформировать последовательность из трех импульсов, представляющих собой положительные полуволны синусоиды. Частота синусоиды 0,5кГц, период следования импульсов 10мс, частота дискретизации 10кГц

>>Fs=10e3;

>> f=500;% частота синусоиды.

>> Ti=1/(f*2); % длительность одной полуволны синусоиды, с частотой в 0,5кГц.

>> ti=0:1/Fs:Ti % интервал длительности одной полуволны от 0 до Ti с шагом 1/Fs.

>> S=sin(2*pi*f*ti);       

>> T=0:1/Fs:0.08;% интервал времени от 0 до любого значения, большего %(периода следования импульса*3+длительность одной полуволны).

>> D=[1:3]'*0.01; %повторение трех полуволн с периодом в 0,01с.

>> Y=pulstran(T,D,S,Fs);plot(T,Y);grid on %Вычисление и построение трех одинаковых положительных полуволн синусоиды с периодом следования 10 и частотой дискретизации 10кГц.

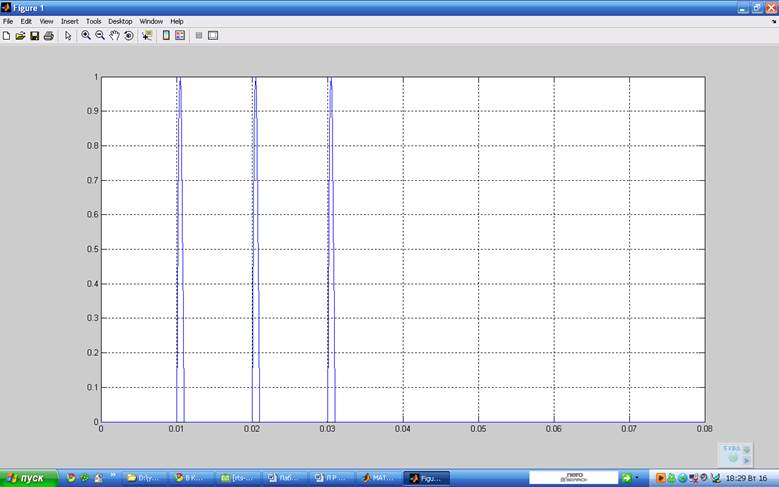
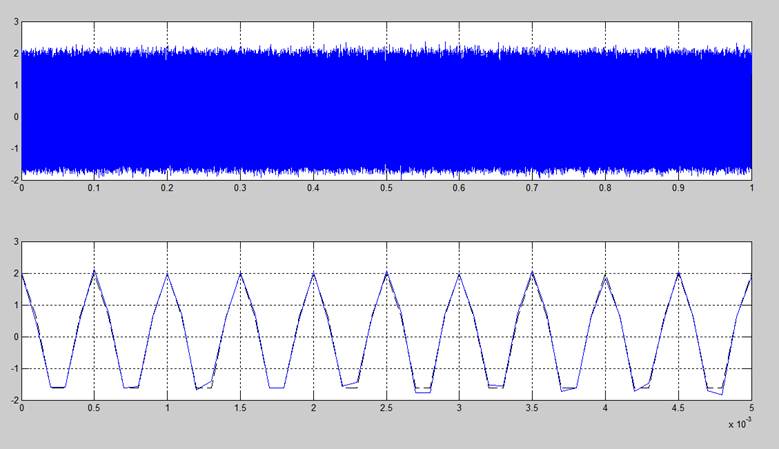
2. Сформировать сигнал, представляющий собой сумму гармонического сигнала с частотой 2кГц и амплитудой 2В и белого гауссова шума, который имеет уровень на 20дБ меньший сигнала. Частота дискретизации 10кГц, интервал времени (0…1)с.

Fs=10e3;    

f=2e3;                   % частота гармонического сигнала

snr=20;        % отношение сигнал\шум

A=2;            %амплитуда гармонического сигнала

t=0:1/Fs:1;   % интервал времени (0..1)с.

x=A*cos(2*pi*f*t);                                     

y=awgn(x,snr,0,'dB');     % добавление к  функции косинуса  белый Гаусовский шум, с отношением сигнал/шум 20 %дБ.

subplot(2,1,1);plot(t,y,'b-');grid on               %построение графиков

subplot(2,1,2);plot(t,x,'k--',t,y,'b-');grid on;xlim([0 0.005])

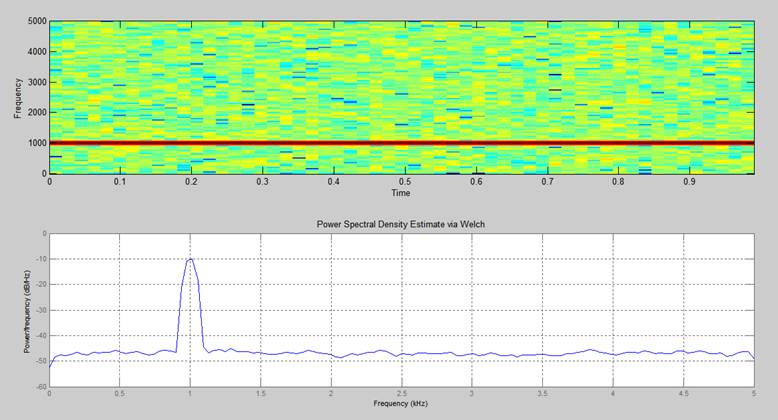
3. Определить спектрограмму и периодограмму сигнала, представляющего собой сумму гармонического сигнала с частотой 1кГц и амплитудой 4В и белого гауссова шума, который имеет уровень на 10дБ меньший сигнала Частота дискретизации 10кГц, интервал времени (0…1)с. Использовать окно Хэмминга длительностью 200 и с перекрытием 20 отсчетов

Fs=10e3;    

f=1e3;                   % частота гармонического сигнала

t=0:1/Fs:1;  

A=4;           

snr=10;       

X=A*cos(2*pi*f*t);

Y=awgn(X,snr,0,'dB');  

subplot(2,1,1);specgram(Y,[],Fs,hamming(200),20)        %Вычисление спектрограммы полученого сигнала (вверху) и периодограммы по методу Уэлча (внизу) subplot(2,1,2);pwelch(Y,200,20,[],Fs)

II. Таблица изученных команд и функций с пояснениями по их использованию