







Методические указания к практическим занятиям
Оглавление.
1. Задание на расчет……………………………………………………..3
2. Передаточная функция разомкнутой системы……………………...4
3. Передаточная функция замкнутой системы………………………...4
4. Дифференциальное уравнение системы…………………………….4
5. Структурная схема замкнутой системы…………………………….5
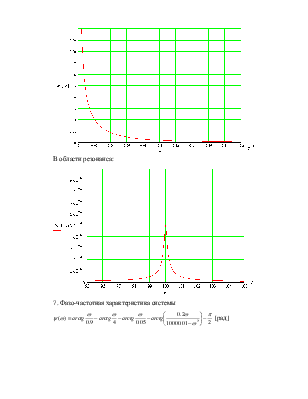
6. АЧХ системы…………………………………………………………5
7. ФЧХ системы…………………………………………………………6
8. АФХ системы…………………………………………………………7
9. Переходная характеристика…………………………………………9
10. Весовая функция ……………………………………………………10
11. Асимптотическую ЛАЧХ и ЛФЧХ………………………………..11
12. Анализ устойчивости системы методом Рауса – Гурвица……….13
13. Анализ устойчивости системы методом Михайлова…………….14
14. Анализ устойчивости системы методом Найквиста……………..16
15. Анализ устойчивости системы при помощи ЛАЧХ и ЛФЧХ…...17
16. Запас устойчивости……………………………………………...…20
Задание на расчет:
По заданным нулю и пяти полюсам передаточной функции разомкнутой системы автоматического регулирования выполнить следующие задания:
· Записать функцию разомкнутой системы
· Записать функцию замкнутой системы
· Записать дифференциальное уравнение системы
· Начертить структурную схему замкнутой системы
· Определить АЧХ системы
· Определить ФЧХ системы
· Построить АФХ
· Определить переходную характеристику
· Определить весовую функцию
· Построить асимптотическую ЛАЧХ и ЛФЧХ
· Проанализировать устойчивость системы методом Рауса – Гурвица
· Проанализировать устойчивость системы методом Михайлова
· Проанализировать устойчивость системы методом Найквиста
· Проанализировать устойчивость системы при помощи ЛАЧХ и ЛФЧХ
· Определить запас устойчивости
2. Запишем передаточную функцию разомкнутой системы:
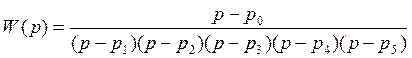 ,
,
Подставив значения корней и полюсов, получим:
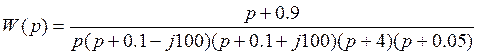 , раскрывая скобки:
, раскрывая скобки:
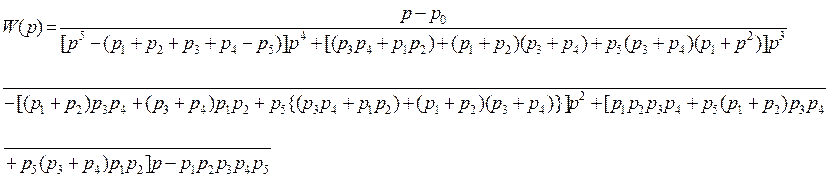
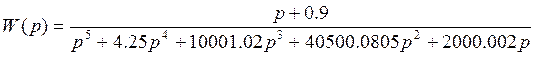 .
.
3. Запишем передаточную функцию для замкнутой системы:
Переход от разомкнутой системы к замкнутой осуществим по
формуле: 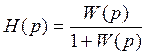 или
или 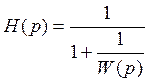 ,
подставляя передаточную функцию разомкнутой системы, получим:
,
подставляя передаточную функцию разомкнутой системы, получим:
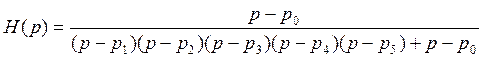 , или
, или
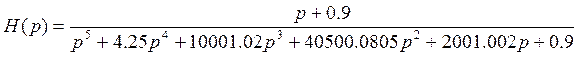 .
.
4. Запишем дифференциальное уравнение для замкнутой системы:
Передаточную функцию можно представить как отклик ![]() на воздействие
на воздействие ![]() , при
этом оператор
, при
этом оператор 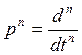 , учитывая вышесказанное, запишем
дифференциальное уравнение:
, учитывая вышесказанное, запишем
дифференциальное уравнение:
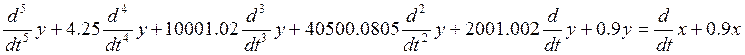 .
.
5. Нарисуем структурную схему замкнутой системы:
Структурная схема замкнутой системы представляет собой разомкнутую систему, охваченную отрицательной обратной связью. Разомкнутая система представляет собой каскадное соединение различных звеньев. Учитывая вышесказанное, нарисуем структурную схему замкнутой системы:
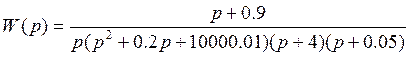 .
.
Структурная схема:

Где ![]() - форсирующее звено;
- форсирующее звено;
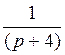 и
и 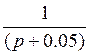 -
апериодические звенья 1-го порядка;
-
апериодические звенья 1-го порядка;
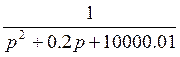 - колебательное звено 2-го
порядка;
- колебательное звено 2-го
порядка;
![]() - идеальное интегрирующее звено.
- идеальное интегрирующее звено.
6. Амплитудно-частотная характеристика системы:
Передаточная функция системы в частотной области может быть
получена заменой ![]() на
на ![]() :
:
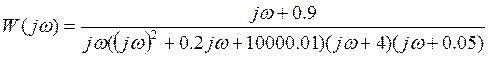
Тогда
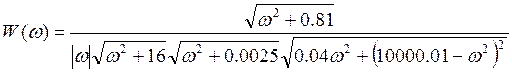
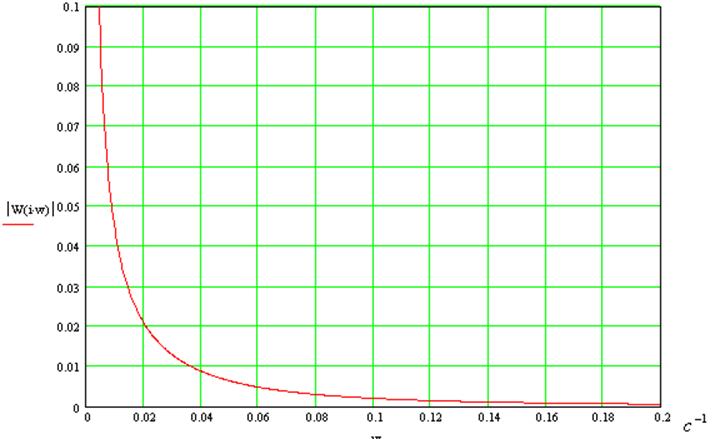
В области резонанса:
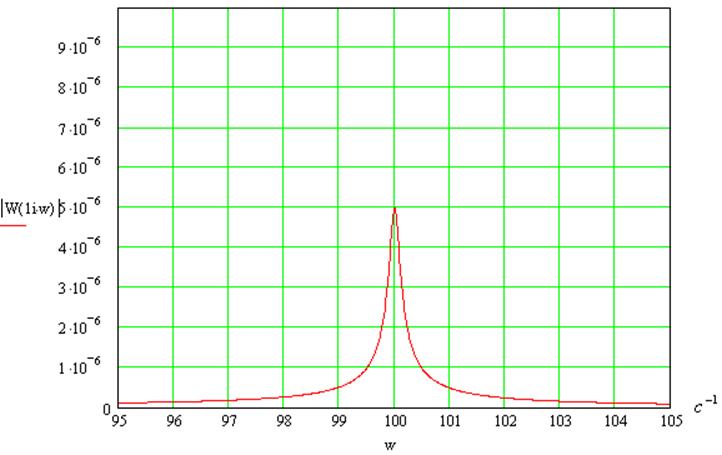
7. Фазо-частотная характеристика системы
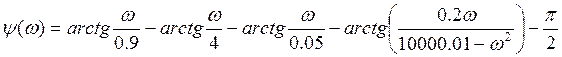 [рад]
[рад]
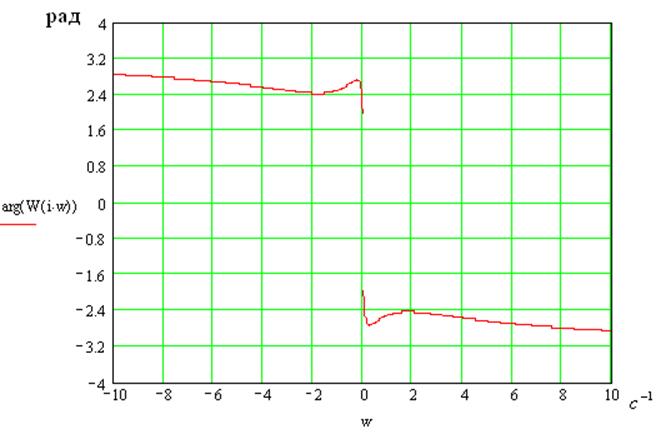
В области резонанса:
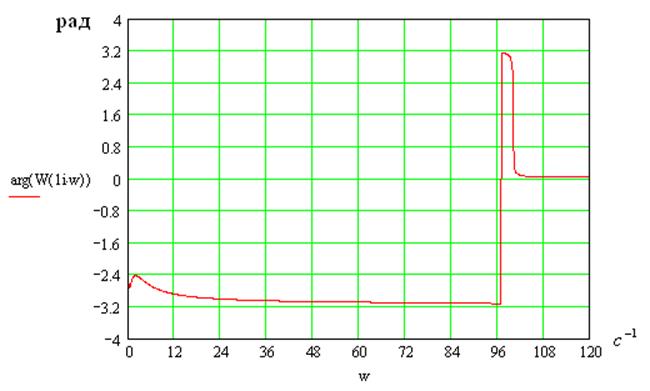
8. Амплитудно-фазовая характеристика системы:
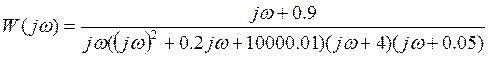
Найдем реальную и мнимую части передаточной функции. Домножим числитель и знаменатель на комплексно сопряженное выражение
![]() , получим:
, получим:
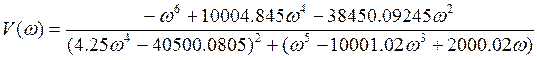 :
:
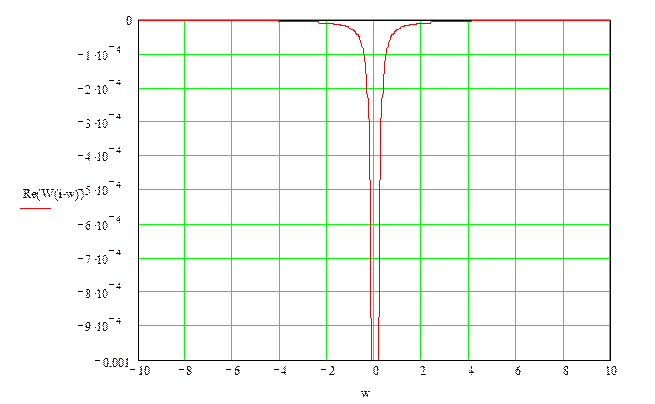
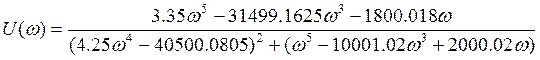 :
:
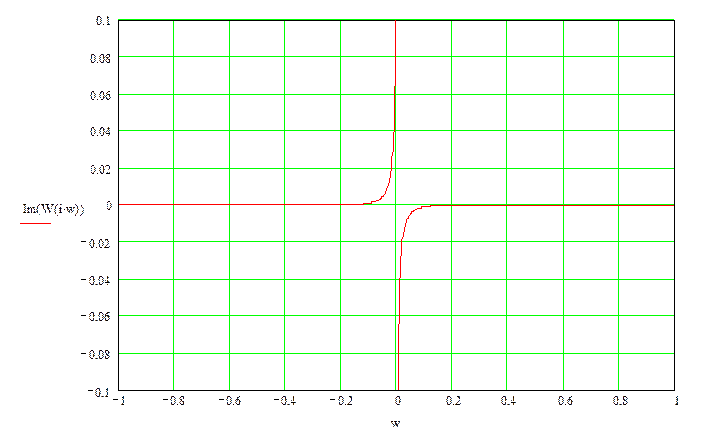
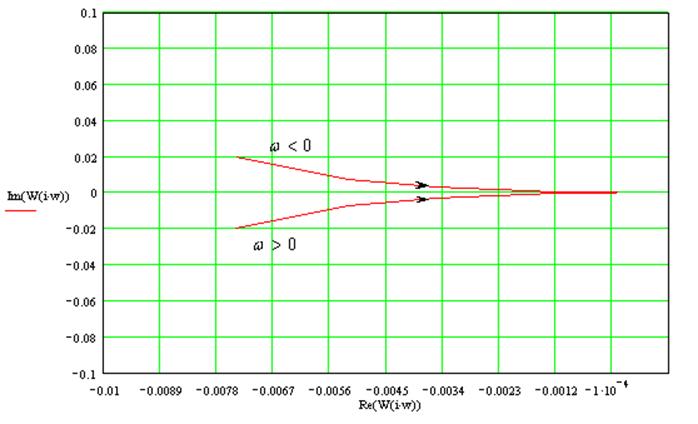
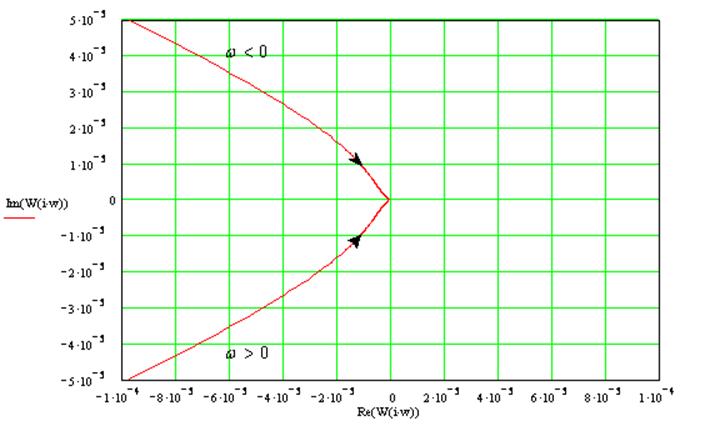
АФХ:
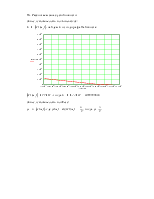
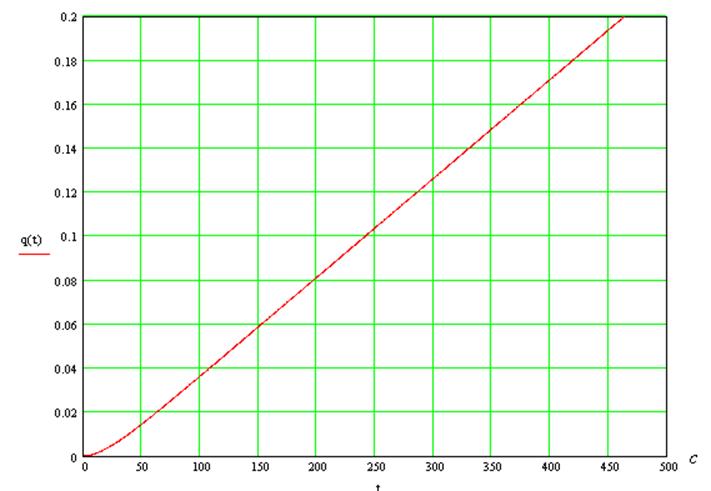
9. Определим переходную характеристику системы:
Переходная характеристика может быть выражена через передаточную функцию системы следующим образом:
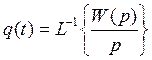 , найдя оригинал от
, найдя оригинал от 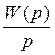 , получим:
, получим:
![]()
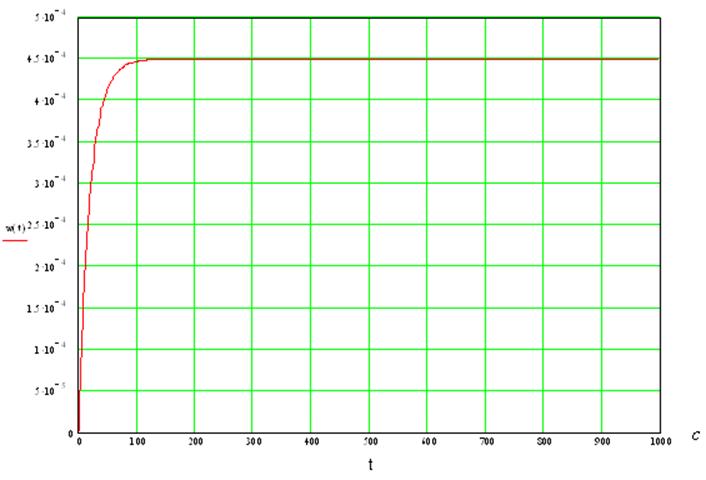
10. Определим весовую функцию, которая может быть выражена через передаточную функцию следующим образом:
![]()
![]()
11. Найти и построить асимптотическую ЛАЧХ и ЛФЧХ:
ЛАЧХ:
![]()
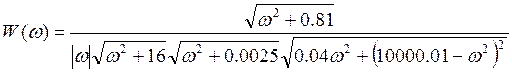 , запишем в другом виде:
, запишем в другом виде:
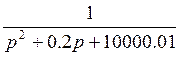 - колебательное звено 2-го
порядка.
- колебательное звено 2-го
порядка.
![]() ;
;
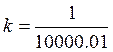 ;
;
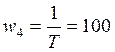 ;
;
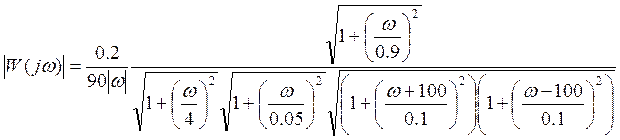 .
.
Сопрягающие частоты:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
Тогда асимптотическую ЛАЧХ можно разбить на следующие интервалы:
При ![]() :
:
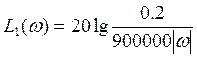 ;
;
При ![]() :
:
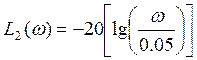 ;
;
При ![]() :
:
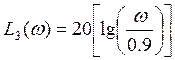 ;
;
При: ![]()
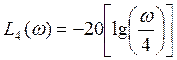 ;
;
При ![]() :
:
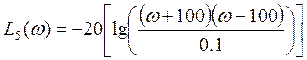 ;
;
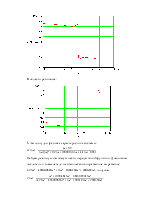
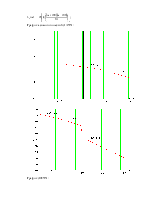
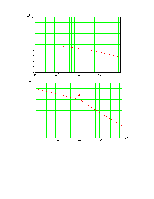
График асимптотической ЛАЧХ:
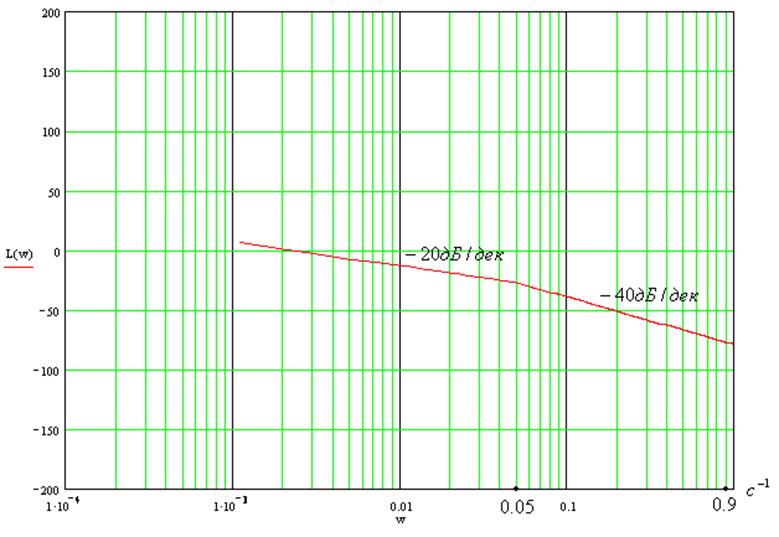
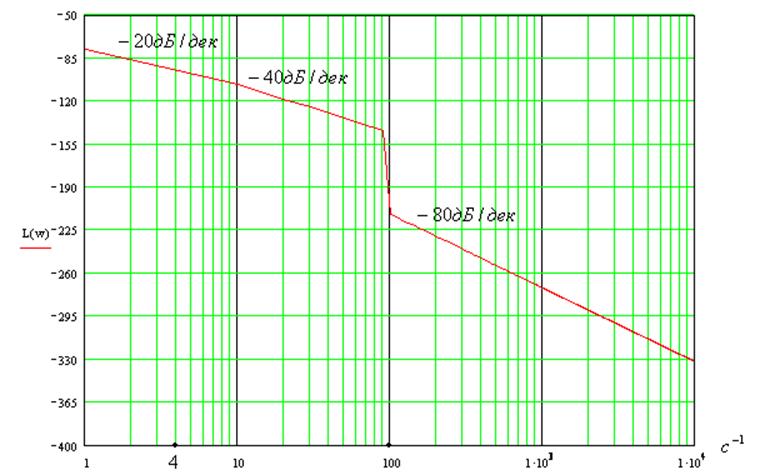
График ЛФЧХ:
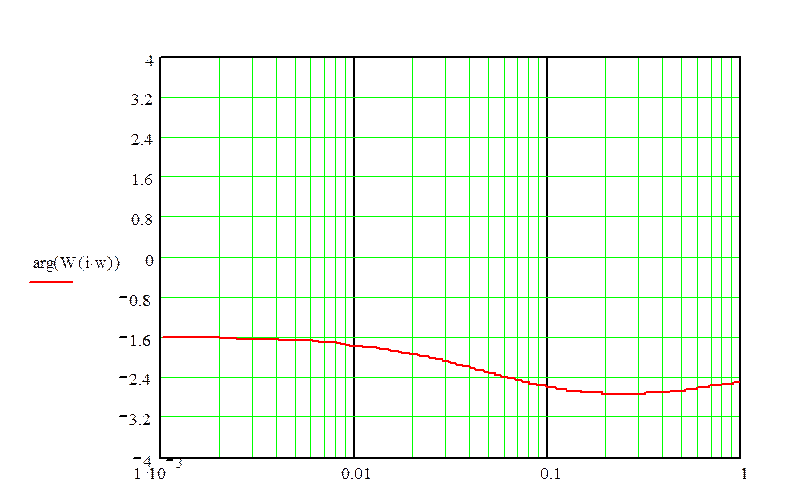
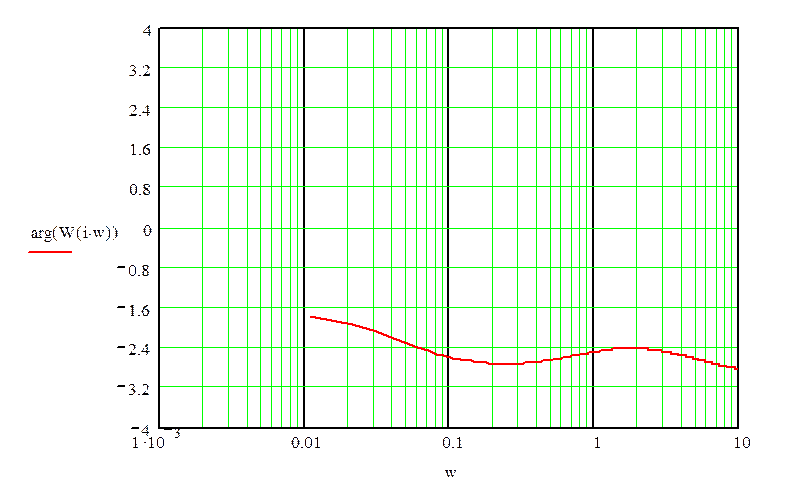 12.
Проанализируем устойчивость системы методом Рауса - Гурвица:
12.
Проанализируем устойчивость системы методом Рауса - Гурвица:
Для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы все определители Гурвица имели знаки, одинаковые со знаком первого коэффициента характеристического уравнения а0, т. е. при а0> 0 были положительными.
Рассчитаем определители, если характеристическое уравнение системы
![]() , тогда:
, тогда:
![]() ;
;
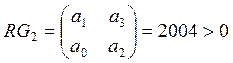 ;
;
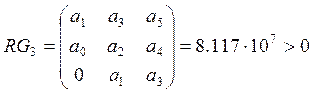 ;
;
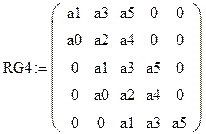
![]()
Так как все определители положительны, система устойчива.
13. Проанализируем устойчивость системы методом Михайлова:
Для того чтобы система автоматического управления была
устойчива, необходимо и достаточно, чтобы кривая (годограф) Михайлова при
изменении частоты ![]() от 0 до
от 0 до ![]() ,
начинаясь при
,
начинаясь при ![]() на вещественной положительной
полуоси, обходила только против часовой стрелки последовательно п квадрантов
координатной плоскости, где п — порядок характеристического уравнения.
на вещественной положительной
полуоси, обходила только против часовой стрелки последовательно п квадрантов
координатной плоскости, где п — порядок характеристического уравнения.
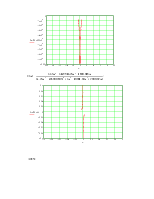
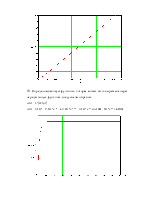
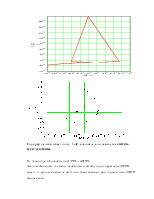
Годограф Михайлова:
![]()
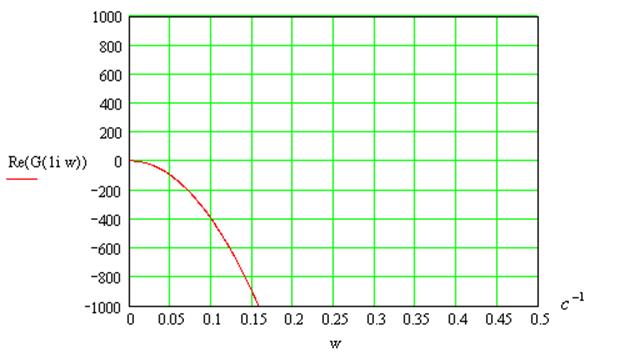
![]()
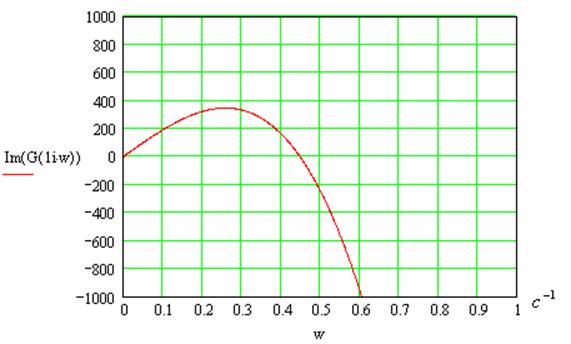
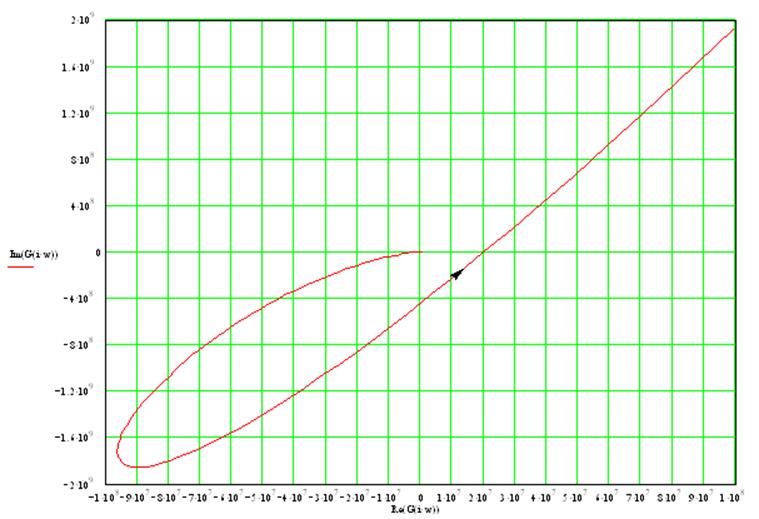
Вектор совершает поворот на 5 квадрантов, следовательно, система устойчива.
14. Проанализируем устойчивость системы методом Найквиста:
Для устойчивости астатической системы 1-го порядка необходимо и достаточно, чтобы годограф разомкнутой системы не охватывал точку -1+j0.
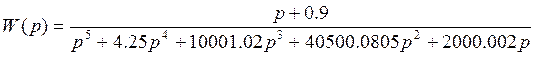 ;
;
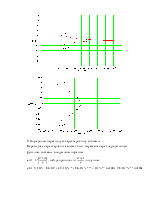
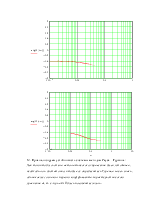
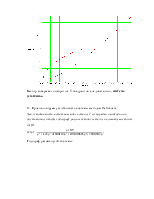
Годограф разомкнутой системы:
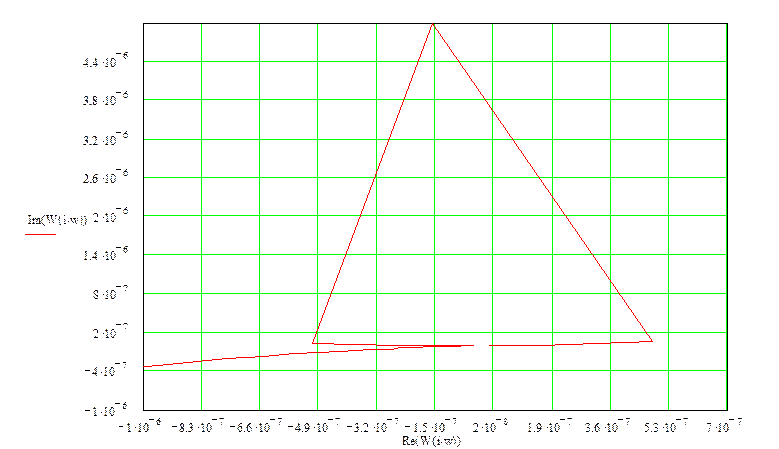
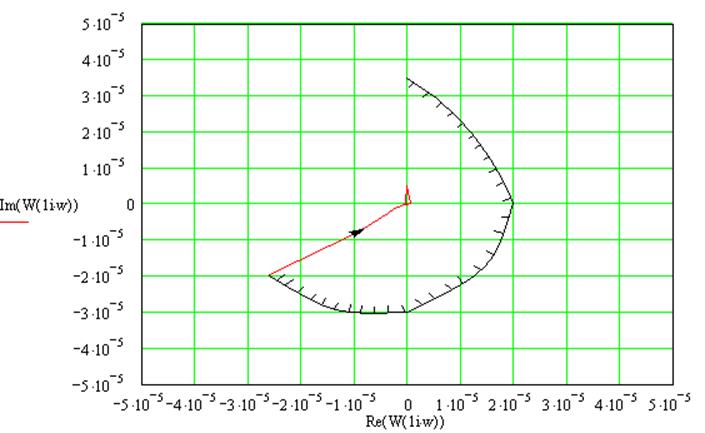
Годограф не охватывает точку -1+j0, следовательно, замкнутая система будет устойчива.
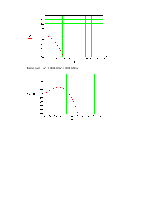
15. Анализ устойчивости по ЛАЧХ и ЛФЧХ:
Для устойчивости системы необходимо, чтобы число переходов
ЛФЧХ через ![]() при изменении
при изменении ![]() от 0 до
от 0 до
![]() было четным, при условии, что ЛФЧХ
было четным, при условии, что ЛФЧХ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.