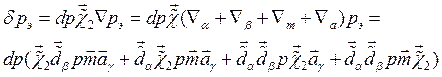, (4.2.4)
где Vq, , V/?, Vm, Va — дифференциальные операторы, действующие соответственно на векторы datp , m, а. В (4.2.4) учтены следующие соотношения, вытекающие из определения оператора (1.1.20): х^хХ = Хг; Х^хХ = Хг ˜
Если вдоль оси 2 и плоскости не направлено четное число векторов da<p, т, а, то, как видно из (4.2.4), во всех слагаемых вдоль указанных направлений окажется нечетное число векторов, ориентированных вдоль хг • Поэтому на основании (4.2.3)
X2Vp3 = 0. (4.2.5)
Таким образом, мы получаем условие равенства нулю производной эффективной упругооптической постоянной, взятой вдоль нормали к плоскости симметрии. Это условие выполнено, когда вдоль оси 2 и плоскости m не направлено четное число векторов из группы datp, т, а, входящей в определение pэ. Заметим, что при выводе (4.2.5) мы воспользовались лишь скалярностью функции pэ. Поэтому указанный вывод может быть отнесен к любой скалярной функции, формируемой из материального тензора, имеющего плоскость симметрии, путем свертки его с векторами. Существенно важным является лишь правило четности, обеспечивающее общую плоскость симметрии у этого тензора и соответствующей полиады векторов, с которой осуществляется свертка. В связи с этим хотелось бы обратить внимание читателей на универсальность сформулированного вывода, приложимого к различным задачам кристаллофизики. Заметим также, что для нечетных операций свертки, с помощью которых, например, образуется эффективная электрооптическая постоянная, можно найти аналогичное условие.
Указанная универсальность соотношения (4.2.5) позволяет без особых доказательств распространить его на другие характеристики акустооптического взаимодействия, в частности, акустооптическое качество M . Это и позволяет нам утверждать, что все рассматриваемые ниже варианты решений могут быть без существенных изменений распространены и на этот случай. Различия сводятся лишь к объему требуемых вычислений. Принципиальные коррективы в схему вычислений при этом не вносятся.
Задача, определенная уравнениями (4.2.1), (4.2.2) и дополненная условием четности ориентированных вдоль оси 2 и плоскости m векторных функций, эквивалентна теперь уравнению:
Хт^Рэ = XmVdadppma-f= 0 , (4.2.6)
где Хт — единичный вектор, лежащий в плоскости симметрии. В остальном этот вектор произволен.
Мы свели задачу поиска экстремумов функции pэ к условию равенства нулю ее производной, взятой вдоль плоскости симметрии m. Остается теперь найти такие решения уравнения (4.2.6) или, иными словами, такие направления векторов в плоскости m, которые удовлетворяли бы уравнениям связи (4.2.2). Из дальнейших разделов этой главы будет видно, что в такой формулировке задача решается относительно просто.
В группу симметрии материальных тензоров конкретного кристалла может войти большое число плоскостей симметрии (подгрупп 2/m). Уравнение (4.2.6) при этом следует решить для каждой из этих плоскостей. Только в этом случае
122
будет найден весь набор экстремальных направлений акустооптического взаимодействия соответствующего кристалла, связанных с его группой симметрии.
Из абсолютной ограниченности функции pэ прямо следует вывод о существовании экстремумов pэ независимо от наличия тех или иных элементов симметрии. По этой причине экстремумы pэ существуют и у кристаллов три-клинной сингонии. Не исключены экстремальные направления, не связанные с элементами симметрии и у высокосимметричных кристаллов. Однако хотелось бы заметить, что в кристаллах, имеющих оси симметрии четного порядка и плоскости симметрии, наличие таких не связанных с симметрией направлений маловероятно.
Дело в том, что анализ аналогичной задачи, относящейся к электрооптическому эффекту и к настоящему времени решенной до конца [ ], показывает, что уже для моноклинных кристаллов, имеющих только одно физически выделенное направление (ось 2 или плоскость m), не связанное с симметрией, решения испытывают определенное влияние элементов симметрии. Для всех кристаллов, имеющих подгруппу mmm, эти решения стягиваются к плоскостям, образующим углы 45◦ с плоскостями симметрии, т. е. фактически также локализованы симметрией. По этой причине у большинства электрооптических кристаллов нет экстремальных направлений, не связанных с симметрией. Дополнительные условия, например, продольности или поперечности электрооптического эффекта, только усиливают ориентирующее влияние симметрии.
Следует заметить, что с ростом числа дополнительных связей, особенно в тех случаях, когда они имеют общую группу симметрии, ее ориентирующая роль усиливается. Естественно поэтому утверждать, что в случае акустооптики, когда решения должны удовлетворять трем различным материальным уравнениям, произвол в разбросе конкретных величин материальных коэффициентов соответствующих тензоров и ориентирующая роль элементов симметрии существенно сильнее сказываются на положении экстремумов, подчеркивая те из них, которые связаны с симметрией, и практически исключая свободные направления.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.