Экстремум заданной функции методом слепого поиска, страница 2

Анализ полученных результатов. Основываясь на данных нахождения экстремума функции  методами дифференцирования, Гаусса-Зейделя и градиента, экстремум должен находиться в точке с координатами х₁=-15, х₂=-20. При этом значение целевой функции у=-41,5. По результатам метода слепого поиска данная точка не является экстремумом (максимумом) целевой функции, т.к. в окрестностях данной точки функция принимает большие значения (например, в точке с координатами х₁=-11, х₂=-11), чем в самой точке. Такое несоответствие результатов, полученных разными методами поиска экстремума, можно объяснить тем, что точка с координатами х₁=-15, х₂=-20 является не явно выраженным экстремумом целевой функции, а точкой перегиба, о чем свидетельствует график поверхности данной функции (рис.1), имеющей вид «седла».

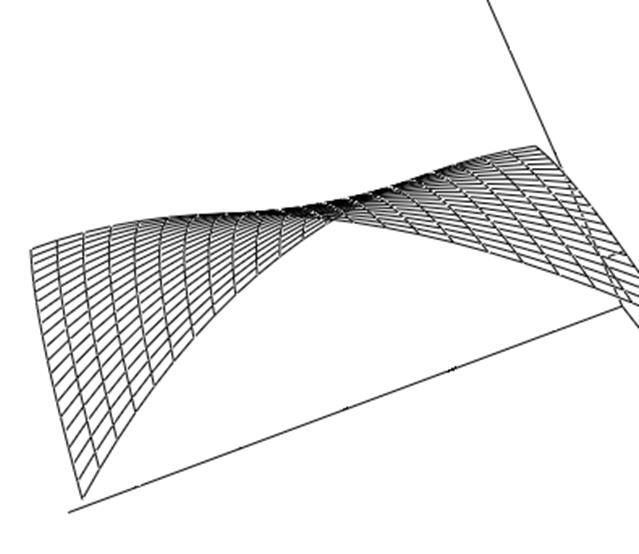
Рис.1

На рис.2 изображена пошаговая реализация метода слепого поиска, причем на рисунке выделены точки, в которых целевая функция принимает значения большие, чем в точке перегиба. Рис.2 представляет собой своего рода двумерный график целевой функции и еще раз подтверждает гипотезу о существовании точки перегиба, а не экстремума целевой функции.

Министерство образования РФ

Владимирский государственный университет

Факультет радиофизики, электроники и медицинской техники

Кафедра конструирования и технологии радиоэлектронных средств

Лабораторная работа №8

по дисциплине: «Математические основы проектирования ЭС»

на тему:

«Оптимизация параметров методом слепого поиска»

Выполнила

Ст. гр. РЭ-101

Шульцева О.В.

Проверил

Талицкий Е.Н.

Владимир 2003