Степенные ряды. Функциональные ряды

Функциональные ряды.

Ряд вида

называется  функциональным. Областью сходимости этого ряда называется множество всех чисел  при которых числовой ряд  сходится.

Примеры 1. Ряд  имеет интервал  своей областью сходимости.

2. Ряд  имеет область сходимости  .

Пусть D - подмножество множества действительных чисел. Говорят, что ряд (1) сходится к функции , определенной на D  равномерно, если для любого  найдется номер N такой, что для всякого натурального  и для всякого выполняется неравенство . Здесь  -- частичные суммы ряда (1).

Пример 3. Имеет место равенство

для любого ; при этом сходимость не является равномерной на всем интервале (-1,1) и даже на полуинтервале , но является таковой на отрезке , где   -- некоторое положительное число меньшее 1.  Действительно, -ый остаток этого ряда выражается и оценивается при  как

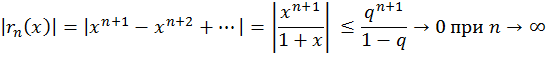
Так как б.м. величина  не зависит от , то функциональный ряд   будет равномерно сходится на отрезке .

Докажем теперь, что ряд  не сходится равномерно на полуинтервале . Это  следует из неограниченности остатка  на полуинтервале . Какое бы  и какое бы натуральное число  мы ни взяли, найдется  достаточно близкое к -1 c условием .

Ряд (1) называется  мажорируемым на области D, если существует сходящийся числовой ряд такой, что  для любого n и для любого .

Предложение.    Мажорируемый ряд сходится равномерно.

Доказательство. Обозначим через  остаток ряда . Для заданного  найдем номер  такой, что  при всех . Тогда для любого  имеет место оценка  □

Теорема.   Если ряд (1) сходится равномерно к функции , и члены ряда  непрерывны, то и функция  непрерывна.

Доказательство вытекает из оценки

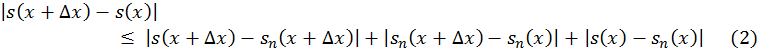
Фиксируем точку . Для заданного  найдем номер  такой, что   при любом  и при любом  Далее, выберем  такое, что     при любом  (пользуемся непрерывностью функции ). Тогда оценка (2) показывает, что   □

Почленная дифференцируемость и интегрируемость функциональных рядов

Теорема 1 (о почленном интегрировании.) Пусть ряд  с непрерывными слагаемыми, мажорируем на отрезке  и сходится к функции . Тогда

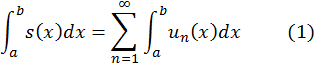
(тем самым числовой ряд в правой части (1) сходится).

Доказательство вытекает из оценки

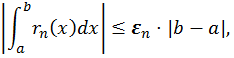
где  -- n-ый остаток мажоранты

Теорема 2 (о почленном дифференцировании).  Пусть , функции  дифференцируемы и ряд  мажорируем на отрезке . Тогда функция  также дифференцируема на отрезке  и имеет место равенство

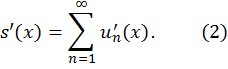
Доказательство.  Обозначим . Тогда по предыдущей теореме

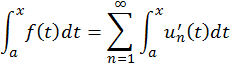
Отсюда следует равенство . Левая часть в этом равенстве  -- дифференцируемая функция, производная которой равна подынтегральной функции. Следовательно,  □

Пример. К ряду нельзя применять теорему 2, так как в результате формального дифференцирования получается расходящийся (например в точке x=0) ряд.

Степенные ряды.

Функциональный ряд вида

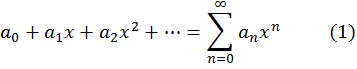
называется  степенным рядом.

Теорема Абеля.   Если ряд (1) сходится при некотором значении , то он сходится абсолютно при любом значении таком, что .  Если же ряд (1) расходится при , то он расходится при любом  модуль которого больше чем .

Следствие.   Существует число  или  такое, что степенной ряд (1) сходится абсолютно при  и расходится при .

Доказательство. Рассмотрим . Множество  не пусто, так как число 0 в него заведомо входит. Если это множество ограничено сверху, то  конечно. В противном случае, полагаем .

Пусть . По определению точной верхней грани, найдется  из множества  такое, что . По теореме Абеля следует абсолютная сходимость ряда в точке . Если , то сходимости в точке  быть не может, ибо иначе  не было бы верхней гранью множества .□

Число R, о существовании которого говорится в следствии, называется радиусом сходимости степенного ряда (1).

Радиус сходимости можно вычислить по одной из следующих двух формул (при условии, что пределы существуют)

 Дифференцирование и интегрирование степенного ряда

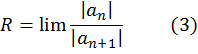
Пусть

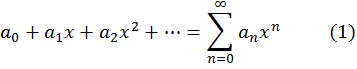
-- степенной ряд с радиусом сходимости R.

Лемма 1.  Ряд (1) мажорируем на любом отрезке [a,b] лежащем в интервале сходимости.

Доказательство. Случай  отбросим как тривиальный. Найдем  такое, что . Тогда  есть мажоранта ряда (1) на отрезке , а значит и на отрезке . □  

Лемма 2.    Ряд , полученный из ряда (1) почленным дифференцированием, имеет тот же радиус сходимости, что и исходный ряд.

Доказательство в предположении, что существует предел отношения  следует из равенств

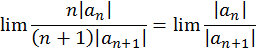
Теорема.  Пусть  -- сумма ряда (1) на интервале . Функция  бесконечно дифференцируема на этом интервале