







Содержание |
Лист |
|
1. Ортогональные преобразования. 2. Основные процедуры используемые в модуле преобразования Фурье. 3. Упрощенный алгоритм программы 4. Примеры рабочих окон 5. Текст основного модуля программы. |
2 3 4 4 9 |
1. ОРТОГОНАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
Реализации, описываемые временными функциями xj(t) не всегда несут полную информацию о наиболее характерных особенностях, используемых при распознавании и идентификации сигналов. Представление сигналов x(t) в виде функционального ряда имеет вид:
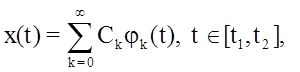
где {jk(t)} - некоторая базисная система ортогональных функций; Сk - постоянные коэффициенты, зависящие от вида {jk(t)}.
Так, спектральное представление в базисе Фурье позволяет распознавать сигналы по положению максимума спектра на частотной оси и ширине полосы. При цифровой обработке сигналов чаще используются ортогональные преобразования в базисах дискретного представления Фурье, дискретное косинусное преобразование, функции Уолша-Адамара, Хаара и др. [6]. Для этих функций разработаны эффективные быстрые алгоритмы расчета на ЭВМ.
Прямое преобразование Фурье может быть записано в виде интеграла:
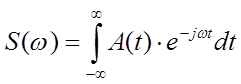 , где
А(t)
– временное представление сигнала.
, где
А(t)
– временное представление сигнала.
![]()
![]()
![]()
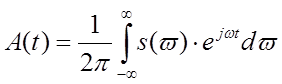 , где
S(w) – спектр сигнала А(t).
, где
S(w) – спектр сигнала А(t).
Дискретное преобразование Фурье прямое (ДПФ) и обратное (ОДПФ) описываются парой:
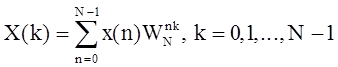
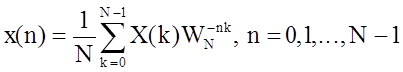 ,
,![]()
где n и k - дискретные время и
частота соответственно; 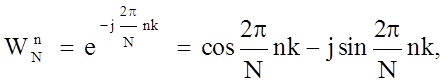 - комплексная дискретная экспонента; N -
размерность ДПФ;
- комплексная дискретная экспонента; N -
размерность ДПФ; ![]()
Расчет спектров ДПФ проводится с помощью алгоритмов БПФ-ОБПФ с прореживанием по времени и частоте. Комплексные спектры ДПФ (БПФ) информативны, так как являются выборками из спектров непрерывных сигналов, и отработаны для практического использования в виде подпрограмм ПК.
2. Основные процедуры используемые в модуле преобразования Фурье.
1. Процедура C_add_mul(C,C1,C2) складывает с числом С результат умножения C1*C2
2. Процедура C_conj(C) делает число С комплексно сопряженным.
3. Процедура C_realdiv(C,Real) делит комплексное число С на действительное
4. Процедура W_init(n) сохраняет комплексные коэффициенты Wn^k=exp(j(2pi * i * k / n)) в массив W_factors [k], 0 <= k < n.
5. Функция W(n,k) выдает рассчитанный коэффициент Wn^k=exp(j(2pi*i*k/n)).
6. Функция radix(n) находит наименьшее число, на которое целочислено делится n.
7. Процедура Split (in,r,m,out) разделяет массив из r * m отсчетов на r частей по m отсчетов, таким образом, что входной массив in[i] преобразуется в out [(i mod r) * m + (i div r)]. Затем вызывается для каждой части преобразование Fourier
8. Процедура Join(in,m,n,out) объединяет n div m частей ( каждая часть содержит м отсчетов) входного массива в выходной массив содержащий n отсчетов. Out [j] является результатом суммы in [j mod m] * W (j * k). Здесь in это k-ый массив in.
9. Процедура Fourier(in,m,n,out) это рекурсивное быстрое преобразование Фурье по методу Кули-Тюки, с любым количеством отсчетов. Скорость алгоритма обратно пропорциональна (n * (r1 + .. + rk)), где k это количество множителей при разложении числа n по степеням, так же это максимальная глубина рекурсии. ri это i-ый множитель.

4. Примеры рабочих окон
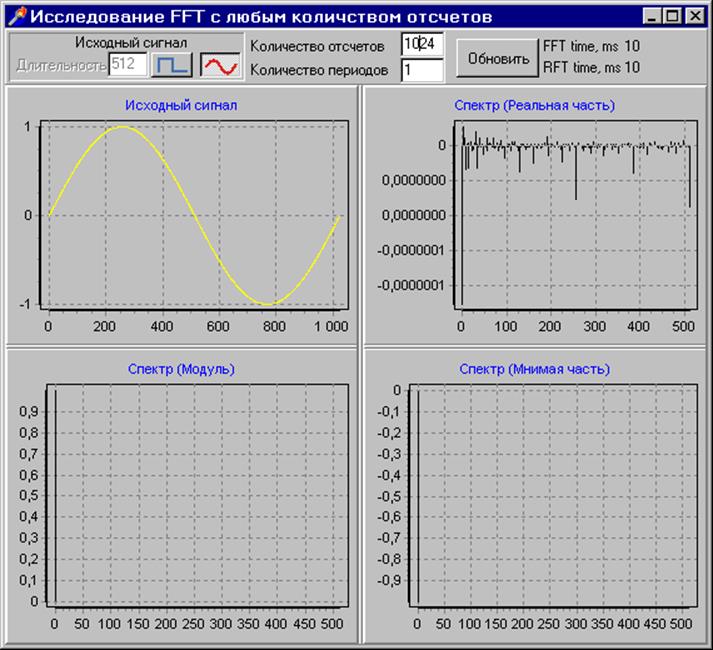
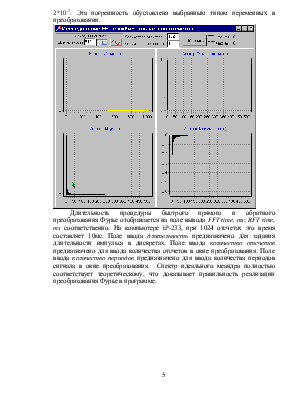
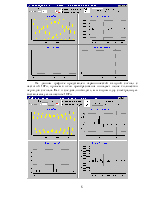
На данном рисунке представлен входной (исходный) гармонический сигнал с частотой 1Гц. После преобразования Фурье модуль спектра имеет одну составляющую на частоте 1 Гц с амплитудой входного сигнала, что полностью соответствует теории. Погрешность по амплитуде не превышает 2*10-7. Эта погрешность обусловлена выбранным типом переменных в преобразовании.
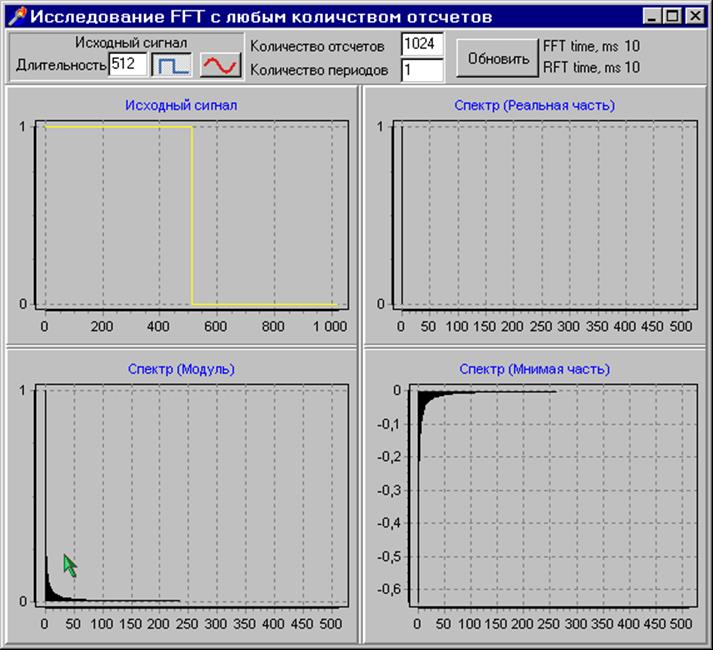
Длительность процедуры быстрого прямого и обратного преобразования Фурье отображается на поле вывода FFT time, ms; RFT time, ms соответственно. На компьютере iP-233, при 1024 отсчетах это время составляет 10мс. Поле ввода длительность предназначено для задания длительности импульса в дискретах. Поле ввода количество отсчетов предназначено для ввода количества отсчетов в окне преобразования. Поле ввода количество периодов предназначено для ввода количества периодов сигнала в окне преобразования. Спектр идеального меандра полностью соответствует теоретическому, что доказывает правильность реализации преобразования Фурье в программе.
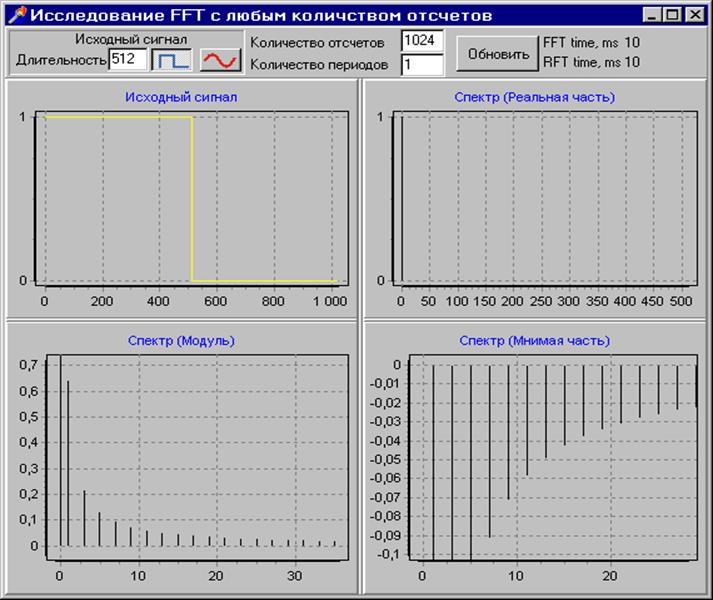
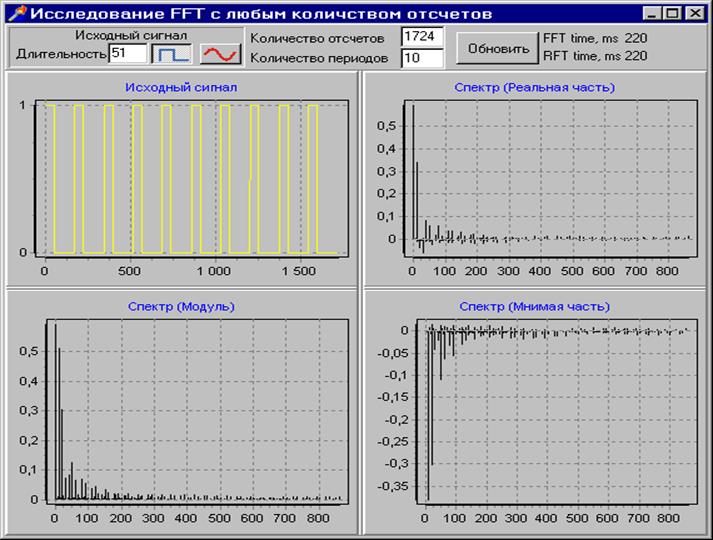
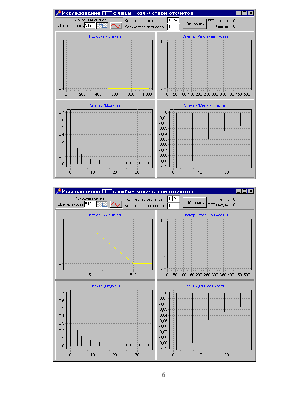
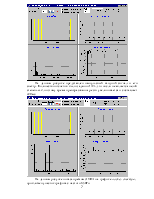
На данном рисунке представлен импульсный входной сигнал и его спектр. Количество отсчетов было заданно 1724, это число не является целой степенью 2, поэтому время преобразования резко увеличивается и составляет 220мс.
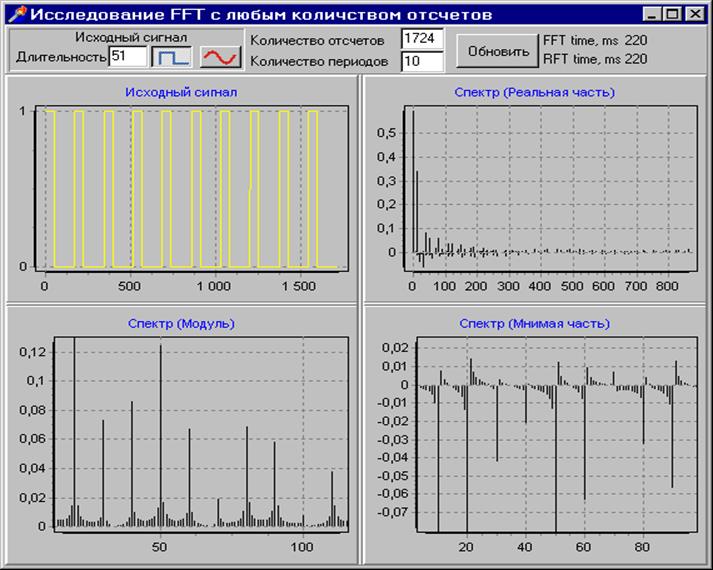
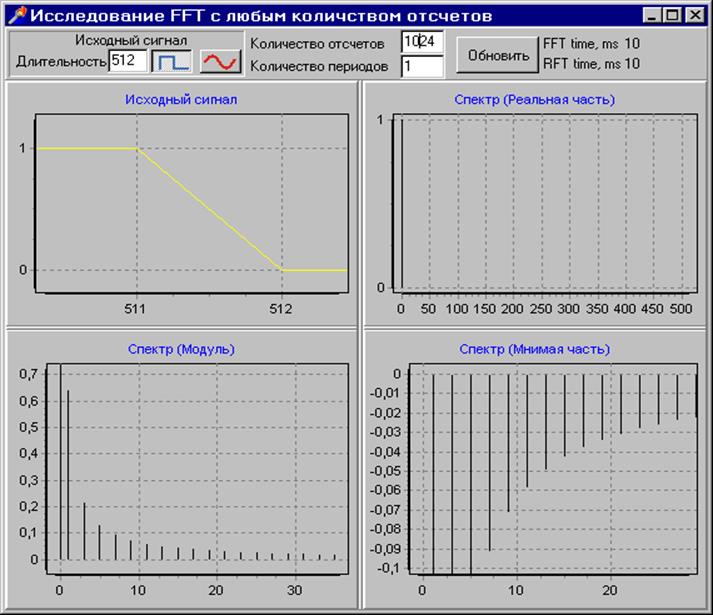
На данном рисунке показан режим ЛУПА на графике модуль спектра, приближен участок графика с частотой 50Гц
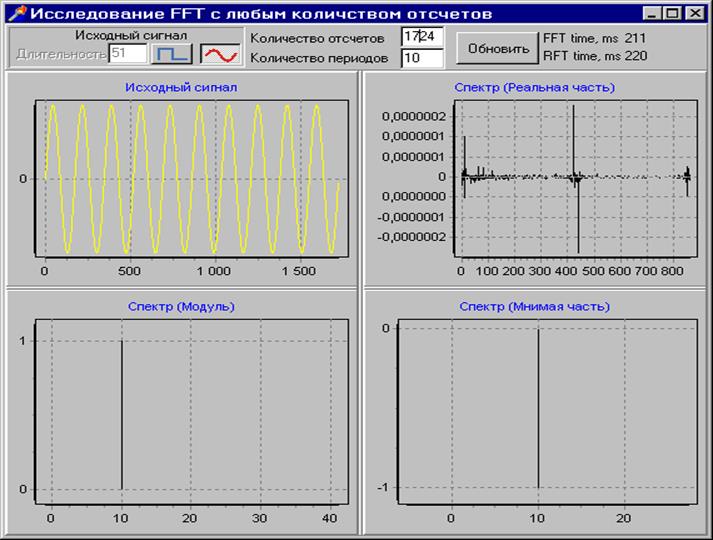
На данном графике представлен гармонический входной сигнал с частотой 10Гц, причем в окно преобразования попадает целое количество периодов сигнала. Как и следовало ожидать, мы видим одну спектральную составляющую на частоте 10Гц.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.