Цифровой фильтр с конечной импульсной характеристикой

косинусное преобразование, функции Уолша-Адамара, Хаара и др. [6]. Для этих функций разработаны эффективные быстрые алгоритмы расчета на ЭВМ.

Прямое преобразование Фурье может быть записано в виде интеграла:

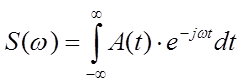, где А(t) – временное представление сигнала.

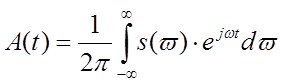                                 , где S(w) – спектр сигнала А(t).

Дискретное преобразование Фурье прямое (ДПФ) и обратное (ОДПФ) описываются парой:

,

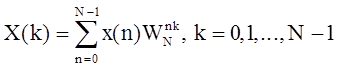
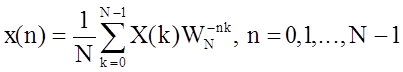где   n  и  k - дискретные время и частота соответственно; 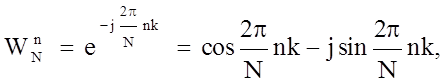 - комплексная дискретная экспонента; N - размерность ДПФ;

Расчет спектров ДПФ проводится с помощью алгоритмов БПФ-ОБПФ с прореживанием по времени и частоте. Комплексные спектры ДПФ (БПФ) информативны, так как являются выборками из спектров непрерывных сигналов, и отработаны для практического использования в виде подпрограмм ПК.

2. Метод взвешивания

Поскольку частотная характеристика любого цифрового фильтра Н(еjw) является периодической функцией частоты, ее можно представить рядом Фурье:

Видно, что коэффициенты Фурье h(п) совпадают с коэффициентами импульсной характеристики цифрового фильтра. Использование соотношения (2) для проектирования КИХ-фильтров связано с двумя трудностями. Во-первых, импульсная характеристика фильтра имеет бесконечную длину, поскольку суммирование в (1) производится в бесконечных пределах. Во-вторых, фильтр физически нереализуем, так как импульсная характеристика начинается в - ¥ , т. е. никакая конечная задержка не сделает фильтр физически реализуемым. Итак, фильтр, рассчитываемый на основе представления функции Н(еjw) рядом Фурье, оказывается физически нереализуемым БИХ-фильтром.

Один из возможных методов получения КИХ-фильтра, аппроксимирующего заданную функцию H(ejw), заключается в усечении бесконечного ряда Фурье (1) за п =  ±  М. Однако простое усечение ряда приводит к хорошо известному явлению Гиббса, которое проявляется в виде выбросов и пульсаций определенного уровня до и после точки разрыва в аппроксимируемой частотной характеристике. Так, например, при аппроксимации стандартных фильтров типа идеального фильтра нижних частот или полосового фильтра максимальная амплитуда пульсаций частотной характеристики составляет около 9% и не уменьшается с увеличением длины импульсной характеристики, т. е. учет все большего числа членов ряда Фурье не приводит к уменьшению максимальной амплитуды пульсаций. Вместо этого по мере увеличения N уменьшается ширина выброса. Поскольку простое усечение ряда (1) не приводит к приемлемой аппроксимации идеального фильтра нижних частот (к чему необходимо стремиться), этот метод непригоден для проектирования КИХ-фильтров.

Алгоритм работы: Y=RFT(FFT(x)*FFT(h))

Лучшие результаты дает метод проектирования КИХ-фильтров, основанный на использовании весовой последовательности конечной длины w(n), называемой окном, для модификации коэффициентов Фурье h(п) в формуле (1) с тем, чтобы управлять сходимостью ряда Фурье. Метод взвешивания иллюстрируется на фиг. 1. Сверху показаны заданная периодическая частотная характеристика Н(еjw) и ее коэффициенты Фурье h(п). Ниже изображена весовая последовательность конечной длины w(n) и ее преобразование Фурье