Федеральное агентство по образованию.
Владимирский Государственный Университет
Кафедра РТ и РС.
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА.
Выполнила: ст. гр. РТС-105
Проверил:
Владимир 2008 г
ЗАДАНИЕ.
По положению нуля и пяти полюсов передаточной функции системы автоматического регулирования выполнить следующие пункты задания:
1. Записать выражения для передаточных функций разомкнутой и замкнутой систем.
2. Записать дифференциальное уравнение системы.
3. Изобразить структурную схему системы.
4. Найти и построить весовую и переходную характеристики системы.
5. Найти и построить амплитудно-частотную и фазочастотную, амплитудно-фазовую характеристики системы.
6. Построить асимптотическую логарифмическую амплитудно-частотную характеристику системы.
7. Проанализировать устойчивость системы методами Рауса-Гурвица, Михайлова, Найквиста и по ЛАЧХ. Привести графики годографов Михайлова и Найквиста.
8. Определить запас устойчивости в случае устойчивой системы или дать рекомендации по обеспечению устойчивости в случае неустойчивой
Исходные данные:
p0= - 1; p1= 0; p2= - 15; p3= - 0, 01; p4= - 2; p5= - 3; K=100
Решение:
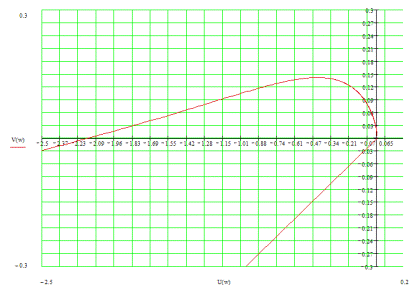
1.Выражение передаточной функции разомкнутой системы:
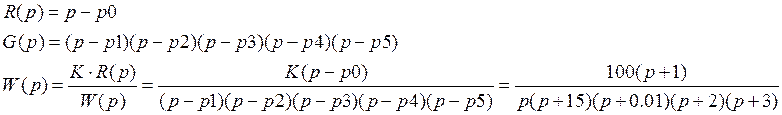
2. Выражение для передаточной функции замкнутой системы может быть получено из формулы:
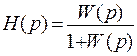 ;
;
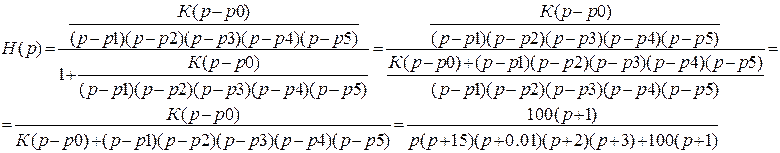
3. Дифференциальное уравнение замкнутой системы:
В дифференциальной форме передаточную функцию системы можно
записать в следующем виде: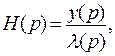 т.е. отношение реакции
цепи на воздействие к этому воздействию.
т.е. отношение реакции
цепи на воздействие к этому воздействию.
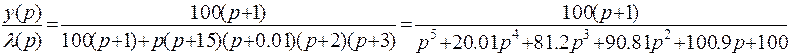
т.е. имеем: ![]()
Учитывая  , получаем
дифференциальное уравнение цепи:
, получаем
дифференциальное уравнение цепи:
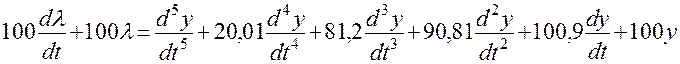
4. Структуру замкнутой системы можно представить в виде разомкнутой системы, охваченной ООС. Разомкнутую систему можно представить в виде включенных последовательно звеньев:
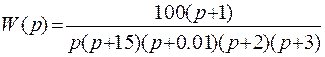
Значит, структурная схема имеет вид:
5. Амплитудно-частотная характеристика системы.
Для получения АЧХ в выражении для передаточной функции разомкнутой системы заменяем p на jω:
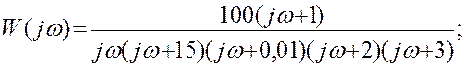
АЧХ системы – это модуль передаточной функции системы:
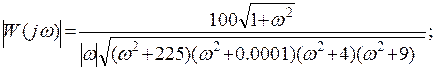
График АЧХ:
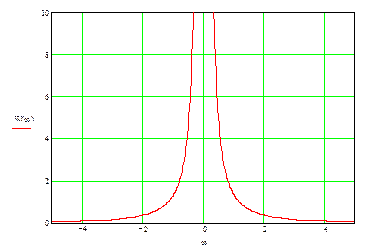
6. Фазочастотная характеристика системы.
ФЧХ системы – это аргумент передаточной функции системы:
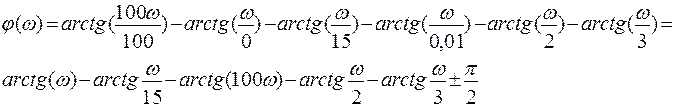
Т.к. в знаменателе стоит p, то будет происходить разрыв при ω=0 на π.
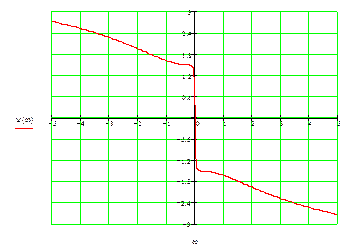
График ФЧХ:
7. Амплитудно-фазовая характеристика системы.
Передаточная функция:
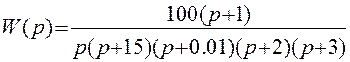 ;
;
В области частот:
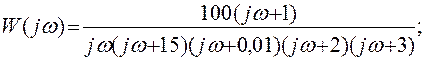
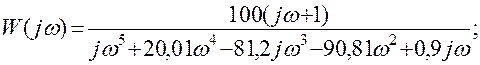
Выделим реальную и мнимую части:
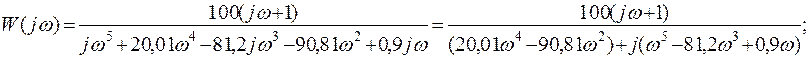
Помножим числитель и знаменатель на ![]()
В итоге получим:
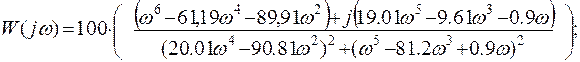
Выделяя реальную и мнимую часть, получаем:
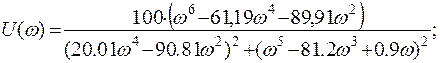
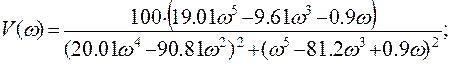
В декартовой системе координат реальную часть принято откладывать по оси абсцисс, а мнимую – по оси ординат.
Построим АФХ:
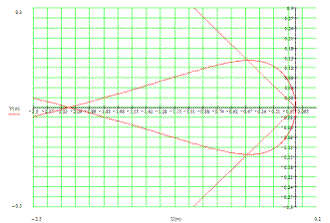
w= 0, 0.01 .. 100
w= 0, -0.01 .. -100

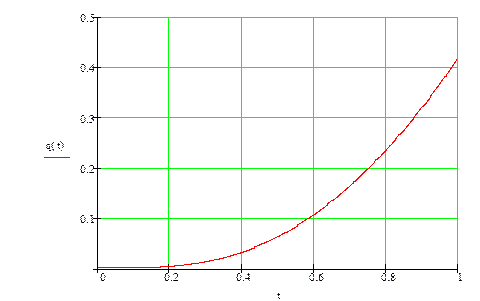
8. Переходная характеристика системы.
Переходная характеристика в операторной форме имеет вид:
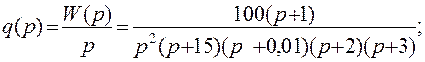
Взяв обратное преобразование Лапласа, получаем переходную характеристику во временной области:
![]()
![]()
Определяется как производная по времени от переходной характеристики: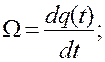

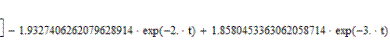
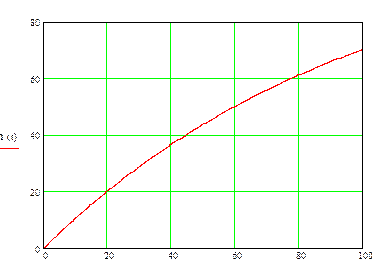
График весовой функции системы:
10. ЛАЧХ и ЛФЧХ системы.
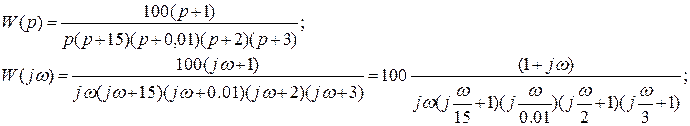
Сопрягающие частоты:![]()
АЧХ имеет вид:
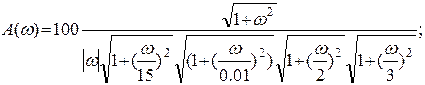
ФЧХ имеет вид:
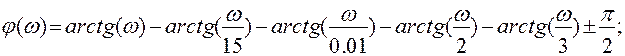
ЛАЧХ имеет вид:
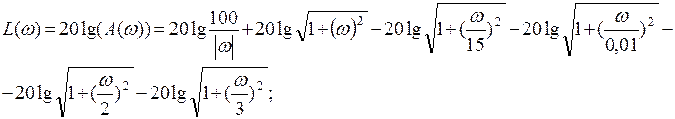
Рассмотрим поведение ЛАЧХ анализируемого звена:
1)
при ![]()
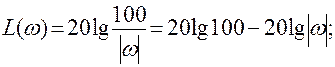
2)
при ![]() :
:
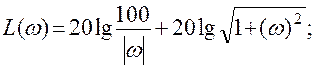
3)
при ![]() :
:
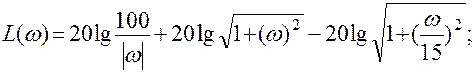
4)
при ![]() :
:
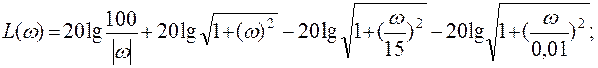
5) при ![]()
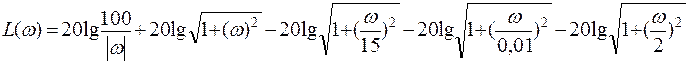
6) при ![]()
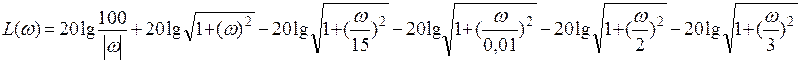
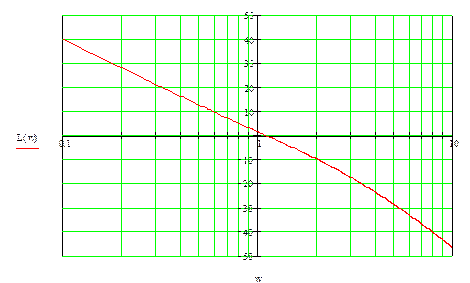
Построим ЛАЧХ:
Построим асимптотическую ЛАЧХ.
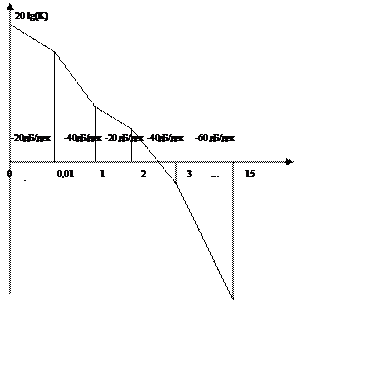
Построим ЛФЧХ:
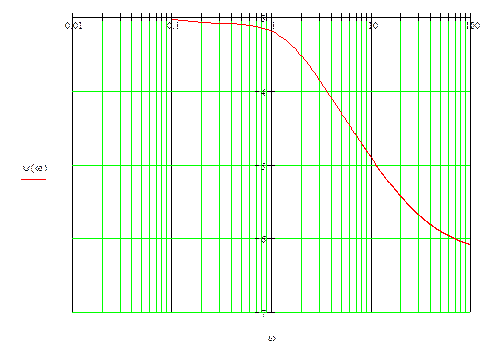
11. Анализ устойчивости системы методом Рауса-Гурвица.
Характеристический полином замкнутой системы:
![]()
Его коэффициенты:
![]()
Матрицы Рауса-Гурвица:
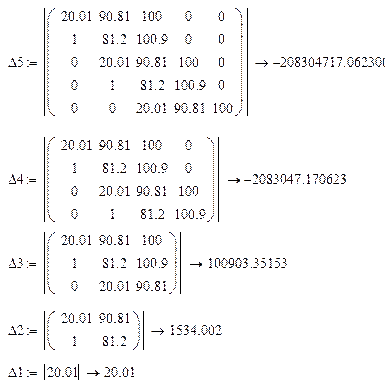
Т.к. первый коэффициент характеристического уравнения отрицательный и определители матрицы отрицательны, то система неустойчива.
12. Анализ устойчивости системы методом Михайлова.
Характеристический полином замкнутой системы в частотной области:
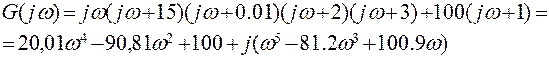
Необходимо, чтобы
сумма аргументов корней равнялась ![]() .
.
Данное условие выполняется: ![]()
Достаточное условие заключается в том, чтобы вектор кривой
Михайлова при изменении частоты от нуля до ![]() повернулся
вокруг начала координат против часовой стрелки на угол
повернулся
вокруг начала координат против часовой стрелки на угол ![]() .
Выделим реальную и мнимую часть:
.
Выделим реальную и мнимую часть:
При построении будем использовать положительные частоты.
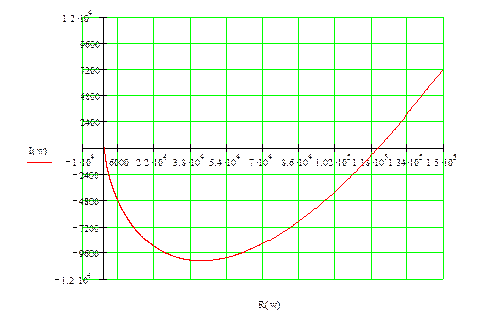
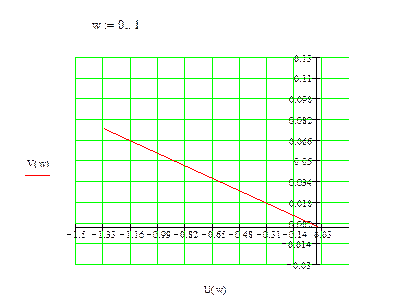
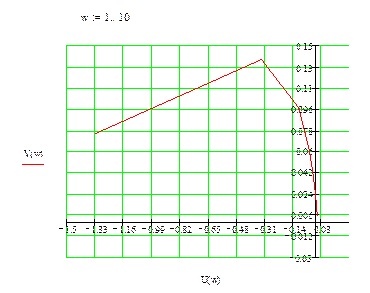
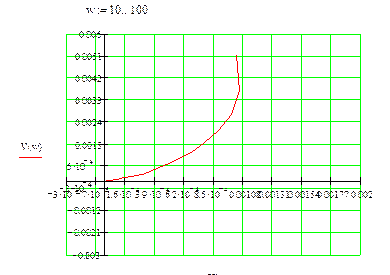
Как видно из графиков, годограф Михайлова при изменении частоты от 0 до ∞ не обходит последовательно квадранты координатной плоскости. Значит, система неустойчива.
13. Анализ устойчивости системы методом Найквиста.
Введем вспомогательную функцию.
![]() , так как
, так как ![]() ,
то
,
то ![]()
Где: 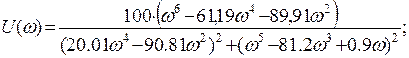

Тогда:
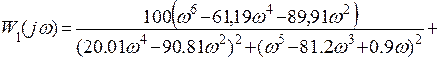
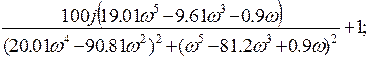
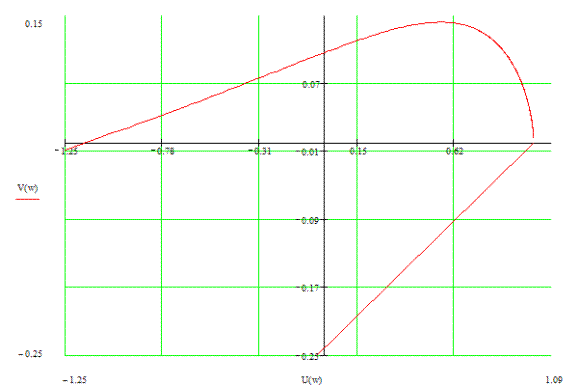
Необходимо и достаточно, чтобы функция в плоскости комплексной переменной была замкнута и не охватывала точку (-1; j0).
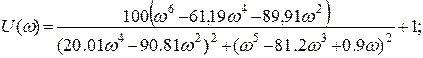
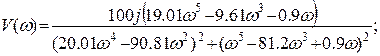
Так как функция терпит разрыв, то система неустойчива.
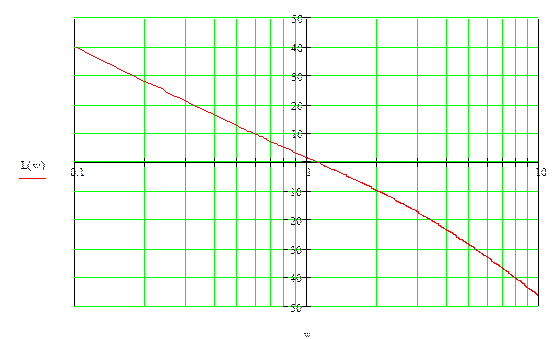
14.Анализ устойчивости системы по ЛАЧХ и ЛФЧХ.
Строим ЛАЧХ:
Строим ЛФЧХ:
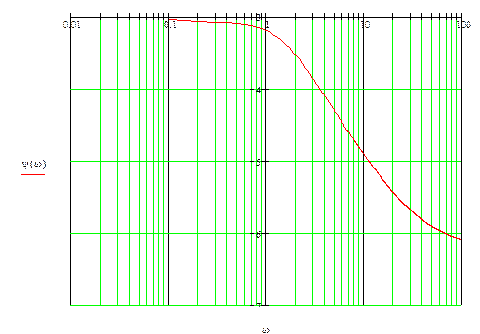
Сопоставляя график ЛАЧХ и ЛФЧХ видим, что при L(A(ω))>0 происходит переход из положительной в отрицательную плоскость. Значит, система неустойчива.
15. Рекомендации по обеспечению устойчивости системы.
Для достижения устойчивости системы необходимо ввести в систему два идеально дифференцирующих звена
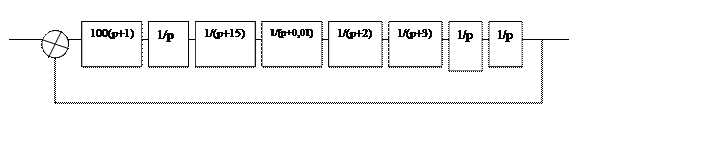
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.