Пассивные микроволновые системы. Теория антенн, страница 3

Тогда эффективная площадь антенны _________________— это такая площадь, что когда излучение со спектральной плотностью _______________ падает в направлении максимальной чувствительности антенны, то принимаемая антенной мощность на единицу частотного интервала будет равна: __________________ (коэффициент 1/2 появляется потому, что излучение случайно поляризовано, а антенна принимает только поляризованное одним видом излучение). Так как изменение чувствительности антенны соответствует диаграмме направленности, а яркостная температура падающего излучения изменяется с изменением направления, то принимаемая антенной мощность на единицу частотного интервала будет равна:

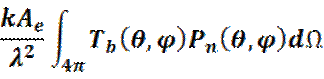
Тогда температура антенны определяется формулой:

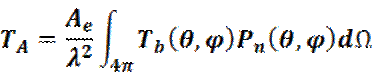
И если сравнить это с уравнением (7.4), то получается простой результат:

Из уравнения (7.9) очевидно, что антенна с большой эффективной площадью обладает маленькой шириной луча и наоборот. Если размеры антенны больше дины волны ___________, то эффективная площадь _____________ будет равна геометрической площади антенны и уравнение (7.9) будет не столь очевидным. Например, если антенна — круглая тарелка с диаметром d, то основной лепесток ее диаграммы направленности будет иметь угловой радиус ___________________ (см. п. 2.7). Отсюда ширина луча будет порядка _________________, а эффективная площадь антенны порядка d². Следовательно, уравнение (7.9) будет выполняться не в полной мере.

Предположим, что антенна направлена на круглую «цель» с яркостной температурой _________, за которым фоновая яркостная температура Т₀. Предположим, что диаграмма направленности равна 1 для всех значений ____________ до некоторой максимальной величины и равна нулю для ______________________ больше этого значения. Тогда антенна будет реагировать равномерно в конусе угла ________________ и не будет реагировать в направлениях вне этого конуса. На рис. 7.3 представлены две ситуации: на рис. 7.3,а цель не распознается, а на рис. 7.3,б распознается, так как у антенны гораздо меньшая угловая ширина луча. Из уравнения (7.4) температура антенны в первом случае будет равна:

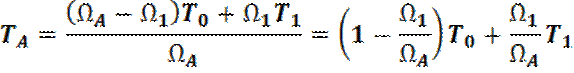
Если антенна будет иметь большие геометрические размеры, то это уменьшит величину угловой ширины луча и улучшит результат определения излучения. Если цель распознается (т. е. ____________________), то температура антенны будет равна:

Важно отметить неожиданный результат: увеличение эффективной площади антенны не приводит к увеличению принимаемой мощности, так как хотя большая антенна может принимать больше излучения, но это осуществляется от меньшего диапазона направлений.

7.2.2. Чувствительность

Определение мощности на единицу частотного интервала, которую фиксирует антенна, через температуру антенны позволяет рассчитать чувствительность антенны, так как мощность шума определяется температурой. Температура шума зависит от компонентов системы, но она не может быть ниже физической температуры, — как правило, температура шума больше физической температуры в 1,2—2 раза.

Чтобы улучшить отношение сигнал/шум, выход микроволнового радиометра интегрируется в некотором отрезке времени ________________. Если полоса пропускания (частотный интервал), в которой принимается излучение, равна ___________, а ___________________________, то отношение сигнал/шум улучшится на коэффициент  ____________________. Тогда чувствительность системы будет равна: