Условия в ветвлениях и циклах. Логические операции в программах

Выяснить отличительную особенность управляющей переменной цикла «до».

4. Детальный разбор задачи

При решении задач циклической структуры в каждой из них можно использовать цикл «до». Особенно актуально такое применение в том случае, когда количество повторов заранее неизвестно. Цикл «до» похож на разветвление.

Задача: Среди чисел  1,   1+1/2,   1+1/2+1/3, ….. найдите первое, больше заданного числа А (А>2). Если номер числа в последовательности меньше 10, то вывести и его.

Выбор и описание переменных.

1	2	3	4
I	Номер числа	Вспомогательное, результат	- натуральное
A	Верхняя грань	Исходное	А>2
X	Искомое число	Вспомогательное, результат	Х>1

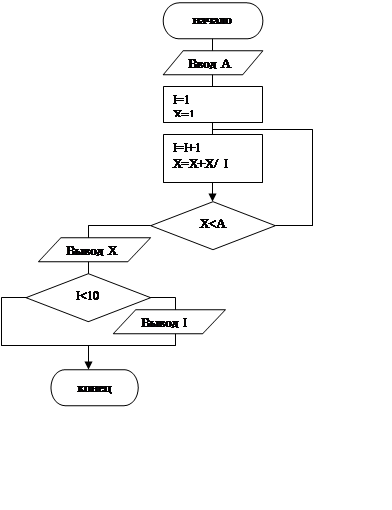Моделирование

Выполнять X=X+1/I до тех пор, пока  X<A. Если I<10, то вывести и номер числа.

Алгоритмизация задачи.

Программирование

INPUT A

I=1

X=1

C:

I=I+1

X=X+1/I                                                                                            нет                                   да

IF X<A THEN GOTO C

PRINT X

IF X<10 THEN PRINT I

END                                                                      нет                                  да

Логические операции, часто используются в ветвлении ( в операторе IF). Они позволяют сочетать в одном условии несколько требований.

Операция                              Название

AND                                       Конъюнкция (логическое умножение)

OR                                         Дизъюнкция (логическое сложение)

NOT                                       Логическое отрицание

Пример: Написать программу, определяющую по длинам сторон А, В и С, является ли треугольник прямоугольным.

INPUT "Введите длину стороны А:";А

INPUT "Введите длину стороны В:";В

INPUT "Введите длину стороны С:";С

А=А^2

B=B^2

C=C^2

IF A+B=C   OR   A+C=B   OR   B+C=A THEN PRINT "Треугольник прямоугольный"

ELSE

PRINT "Треугольник не прямоугольный"

END IF

END

Решение задач по карточкам С-6, С-7

Домашнее задание: Написать программу, определяющую по длинам сторон А, В и С, является ли треугольник равнобедренным.

50. Конструирование алгоритмов методом пошаговой детализации. Вспомогательный алгоритм (тесты)

Цели урока:

1.  изучить понятие "вспомогательный алгоритм" рассмотреть его роль в создании модульной программы, через современные методы организации программ;

2.  способствовать развитию логического мышления, интеллектуальных способностей;

3.  воспитывать умение выражать свои мысли, аккуратность, точное соблюдение выполнения алгоритма.

План урока:

1.  Изучение новой темы

2.  Закрепление нового материала

3.  Подведение итогов. Домашнее заранее.

Ход урока:

1. Алгоритм — это организованная последовательность конечного числа точных и понятных действий, необходимых для решения любой задачи данного класса.

Эффективным методом построения алгоритмов является метод пошаговой детализации (последовательного построения). При этом сложная задача разбивается на ряд более простых. Для каждой подзадачи составляется свой, относительно решения основной задачи, вспомогательный алгоритм. Требования к ним продиктованы необходимостью как решения подзадачи, так и последующей их "стыковки" в основном алгоритме. Эти подзадачи могут, в свою очередь, потребовать разбиения на еще более простые задачи, и т. д. В результате некоторые вспомогательные алгоритмы могут стать основными по отношению к вспомогательным алгоритмам более низкого уровня. Процесс пошаговой детализации заканчивается, когда задачи очередного уровня окажутся совсем простыми. Метод пошаговой детализации универсален. Он применим для решения задач из разных областей жизни. Метод пошаговой детализации путем разбиения задачи на подзадачи лежит в основе так называемого структурного программирования

Причины использования  вспомогательных алгоритмов:

Ø  разбиение более сложной задачи на ряд более простых задач

Ø  многократное использование одного и того же набора действий в одном или разных алгоритмах.

Вспомогательные алгоритмы, как уже отмечалось, должны быть состыкованы между собой в процессе "сборки" основного алгоритма. Для этого используют заголовки вспомогательных алгоритмов; с их помощью вызывают этот алгоритм (обращаются к его работе) из других вспомогательных или основного алгоритмов.

Вспомогательные алгоритмы применяют для программ анализирующих значения(тесты), вводимые пользователем, такая программа может:

1.  задать пользователю вопрос;

2.  получить ответ;

3.  проанализировать его;

4.  вывести на экран сообщение (результат);

5.  повторять при необходимости эти шаги столько раз сколько нужно.

При составлении и использовании вспомогательных алгоритмов важно знать, что является для них

Ø  исходными данными (аргументами) это имена переменных, которые вносят