Применение вейвлет –анализа в задаче оценки регрессии. Основные определения

асс. кафедры информатики ФГБОУ ВПО «АмГПГУ»

Применение вейвлет –анализа в задаче оценки регрессии

Основные определения

Регрессия – это зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин. В отличие от чисто функциональной зависимости , когда каждому значению независимой переменной x соответствует одно определённое значение величины , при регрессионной связи одному и тому же значению  могут соответствовать в зависимости от случая различные значения величины .

Пусть существует зависимость  переменной  от переменных .

Переменные  называются предикторами, это те переменные, для которых можно устанавливать желаемые значения или те которые  можно только наблюдать, но не управлять ими.

Зависимая переменная , или переменная отклик, это такая переменная, которая изменяется в результате изменений переменных .

Классическая схема регрессии- это случай, когда значения  детерминированы, предопределены.  Обычно в этом случае значения переменной   расположены равномерно.

Стохастическая схема регрессии - это случай, когда значения  являются результатами измерений, обработки или случайно выбраны. Обычно значения   располагаются нерегулярно.

Пары случайных чисел   имеют двумерное распределение  вероятностей некоторого типа. Если связь между зависимой случайной величиной  и величиной , которая не является случайной переменной, установлена, то уравнение  относительно  будет назваться уравнением регрессии.

Изображение чисел  на графике называется диаграммой рассеивания или точечной диаграммой.

Для случая n независимых переменных сложно изобразить диаграмму рассеивания, так же существует сложность определения принадлежности точки  заданной области.

Оценивание регрессии

Сначала по данным  строится регрессионная поверхность, а затем, зная эту зависимость и новый набор независимых переменных  оцениваются значения зависимой переменной .

Использование вейвлет-анализа

В системе Matlab реализован случай , по следующему алгоритму:

1.  Преобразование данных  в данные, используя процедуру разбиения области значений на малые промежутки. Значения равномерно распределены. Для каждого промежутка  определяем:

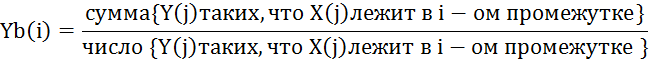
2.  Делаем вейвлет-разложение сигнала , используя быстрые алгоритмы. Здесь предполагается, что  данные есть 1,2,…,nb , где nb – число промежутков;

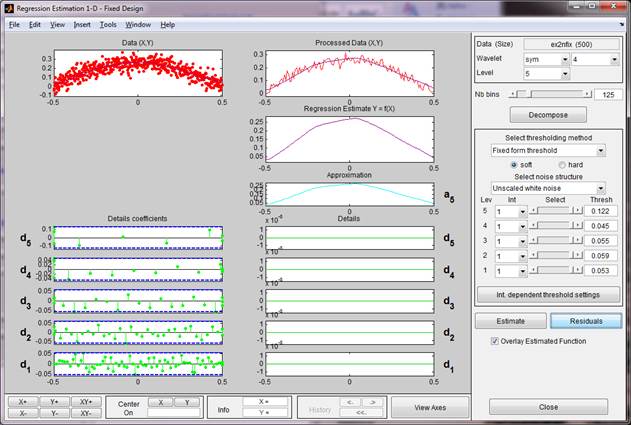
рис.1. реализация одномерной регрессии в Matlab.

3.  Делаем пороговую обработку вейвлет-коэффициентов;

4.  Восстанавливаем оценку  функции  из обработанных вейвлет-коэффициентов, используя быстрые алгоритмы;

5.  Перемасштабируем результирующую функцию  , преобразовывая 1,2,…,nb в данные , и интерполируем  в каждом промежутке, чтобы найти оценку .

Расширив этот алгоритм до случая n-переменных , возможно, реализовать  многомерную регрессию.

Библиографический список:

1.  Дрейпер, Н., Смит, Г. Прикладной регрессионный анализ. Перевод с английского Адлера , Ю.П.,Горского, В.Г. М. «Финансы и статистика» 1986 книга 1.

2.  Смоленцев Н.К. Основы теории вейвлетов. Вейвлеты в MATLAB.М.: ДМК, 2005. – 305 с.

3.  www.mathworks.com