Недостатком антенны является малая эффективность преобразования ¾ доля энергии первичного излучения, переходящая в энергию низкочастотного (НЧ) колебания. Согласно соотношению Мэнли-Роу, преобразование с существенным понижением частоты при взаимодействии трёх плоских волн позволяет получить максимальную эффективность преобразования по энергии h2=W2/2×w2. Оценки, проведённые с учётом дифракции первичных и вторичных полей, в наилучших условиях приводят с точностью до коэффициента порядка единицы к тем же результатам. Во многих приложениях с малой энергетической эффективностью можно было бы мириться, если бы при этом можно было получить достаточно мощное излучение низкой частоты. Здесь, однако, возникают трудности, связанные с тем, что интенсивность первичного излучения антенны принципиально ограничена тем, что в отсутствие дисперсии формирование периодических слабых разрывов в первичных волнах приводит к резкому увеличению их затухания. При этом антенна насыщается, дальнейшее увеличение интенсивности уменьшает эффективную длину антенны, и она постепенно теряет своё основное достоинство ¾ острую характеристику направленности. Эти весьма противоречивые свойства акустической излучающей параметрической антенны и привлекли к ней значительное внимание. Следует отметить, что в некоторых приложениях отмеченные выше преимущества антенны преобладают над её основным недостатком ¾ малой эффективностью.
Теория параметрической антенны сложна из-за того, что в настоящее время решение задач о дифракции нелинейных волн представляет значительные трудности. Тем не менее, имеется ряд приближённых решений, позволяющих не только разумно выбирать параметры антенны, но и проводить вполне удовлетворительно согласующиеся с экспериментом расчёты.
Первая квазидвумерная теория антенны была предложена Вестервельтом. Теория основывалась на том, что одномерные уравнения нелинейной акустики в приближении более высоком, чем первое, представляют собой неоднородные волновые уравнения с известной из решений уравнений более низкого приближения неоднородностью. Уравнение второго приближения ¾ уравнение с источниками, распределение которых определяется первичным полем. Последнее в теории предполагалось в виде узкого коллимированного пучка. Применение метода запаздывающих потенциалов позволило получить в дальнем поле
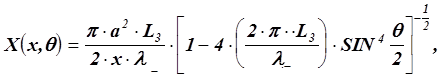
где Х – функция осевого распределения вторичного поля;
–
апертура источника первичных волн.
Полуширина характеристики направленности для длинной антенны (Lз›› l– ) равна
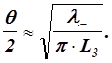
Ограничения теории Вестервельта достаточно сильные:
1. Не
учитывалась дифракция первичного поля и поперечное распределение
вторичных источников. Это, по существу, и позволило использовать одномерную
систему уравнений, искусственно вводя „двумерность” при отыскании второго приближения.
Очевидно, что такое рассмотрение становится возможным при Lз/Lд<<1
(Lд – расстояние дифракции волн накачки) и <<
;
при этом параметр ND=Lз/LдФ <<1 (Ф=w/W –
снижение по частоте). Этот параметр играет существенное значение для
параметрических антенн при учёте дифракционных эффектов.
2. Исключено из рассмотрения ближнее поле вторичного излучения. Хотя, как правило, в приложениях представляет больший интерес характеристики в дальнем поле, в период исследования антенн и для выбора наилучших условий её работы значительный интерес представляет процесс формирования параметрического излучения.
3. Приближённый характер теории очевиден из того, что использовалось второе приближение, и, следовательно, теория применима лишь для маломощных первичных пучков.
Это привело к тому, что как по уровню излучения, так и по ширине характеристики направленности полного соответствия теории с экспериментом не было. В частности, при некоторых экспериментальных условиях характеристика направленности оказывалась уже, чем это следовало из формулы. Нужно, однако, сказать, теория Вестервельта оказала значительное влияние на развитие представлений об антенне. Совершенствованию этой теории посвящено значительное число работ. В частности, в некоторых работах было учтено поперечное распределение вторичных источников. В значительном числе работ исследовались более сложные модели первичного поля, чем коллимированный пучок: сферически расходящаяся направленная волна, коллимированный пучок в ближнем поле и конус сферически расходящихся волн — в дальнем. На основе модельных представлений о первичном поле проведены также расчёты ближнего поля антенны.
Принципиально новая теория антенны, естественным образом учитывающая нелинейную дифракцию трёхмерных волн, стала возможной на основе решения уравнения Хохлова-Заболотской для нелинейных звуковых пучков. Это позволило получить теорию антенны, практически свободную от ограничений теории Вестервельта. В первой из работ этого направления рассматривалась задача о параметрическом излучении в ближней зоне при х<Lд , то есть не учитывалась дифракция первичного излучения. В дальнейшем был рассмотрен боле общий случай, учитывающий дифракцию как вторичного, так и первичного полей. В результате получено интегральное представление формирования и излучения низкочастотной волны. Это представление в большинстве практически интересных случаев существенно упрощается для осевых распределений низкочастотного излучения и может быть найдено в явном виде.
Сложная взаимосвязь нелинейных, дифракционных и диссипативных эффектов в параметрической антенне приводит к необходимости оптимизации параметров антенны для получения наибольшего уровня излучения при сохранении острой характеристики направленности. Оптимизация, естественно, определяется и акустическими параметрами среды, в частности, антенна из-за меньшего затухания лучше работает в воде, чем в воздухе, что согласуется с экспериментом. Если не заданы какие-либо специальные дополнительные условия, то в воде оптимальные первичные частоты лежат в области 104-105 Гц; на более низких частотах резко увеличивается оптимальный диаметр источника, более высокие частоты быстро затухают и длина антенны становится слишком малой.
Все эти свойства позволяют практически реализовать параметрические антенны и преобразователи, обладающие широкой полосой рабочих частот, малыми габаритами, постоянной и гладкой характеристикой направленности на различных частотах. Изменяя частоты f1 и f2 электрических сигналов в пределах резонансной кривой преобразователя накачки, можно добиться плавной перестройки частоты F в широких пределах ( коэффициент перекрытия достигает 300 и более ). С помощью нелинейных параметрических приборов решается важная проблема: широкополосное излучение и приём. Однако обеспечение этих качеств связано с большими энергетическими затратами. Тем не менее, в целом ряде случаев применение параметрических антенн является более эффективным даже с точки зрения энергетических затрат по сравнению с традиционными устройствами.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.