Проверить является ли пара матриц управляемой/ Критерий управляемости

Задания 3-4. Пример 25. Проверить является ли пара матриц A2 и A11 управляемой.

Решение:

Для проверки стабилизируемости воспользуемся следующими критериями (из лекций):

Критерий управляемости. Пара A, B управляема ó обе пары A, B и A, -B являются                            стабилизируемыми.

Критерий стабилизируемости. Пара A, B стабилизируема ó Re λ_i (H) ≠ 0, где

.

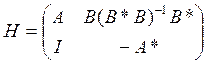Заметим, что , поэтому достаточно проверить критерий стабилизируемости только для пары матриц A2 и A11.  

Проверим, не попадают ли собственные значения матрицы Н на мнимую ось, воспользовавшись алгоритмом круговой дихотомии для  матрицы A = e^tH

Применим к ней алгоритм круговой дихотомии для матричного пучка A – λI. Расчеты выполним в системе Matlab. В результате расчетов норма H в критерии дихотомии равна 1.9152e+003, следовательно, матрица H из критерия стабилизируемости не имеет собственных чисел на мнимой оси, значит, пара A2, A11 – управляема.

Проверим результаты расчетов, построив графики функций z(x, y) = ln ( σ_min (H – (x + iy) I )) и z1(y) = ln ( σ_min (H –iy I )) (на мнимой оси)  на сетке x = -5: 0.05: 5,  y = -5: 0.05: 5, чтобы посмотреть, как ведет себя ε-спектр матрицы H.

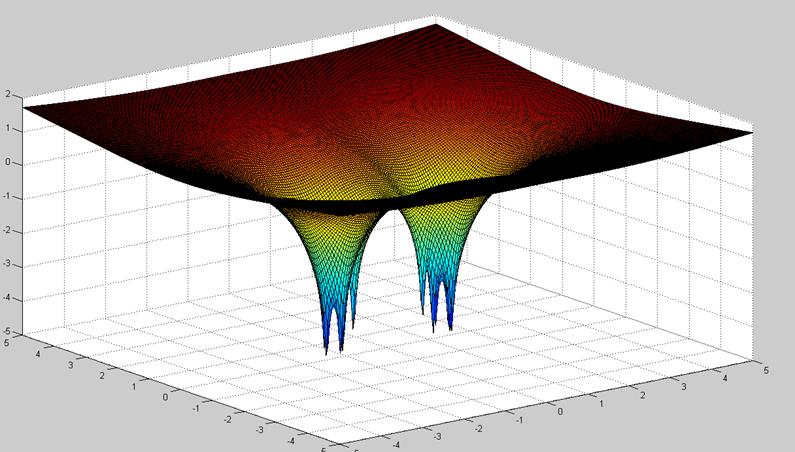
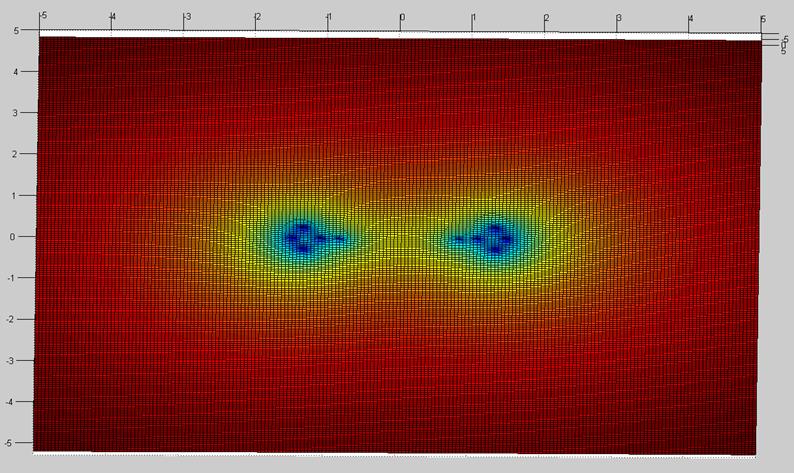
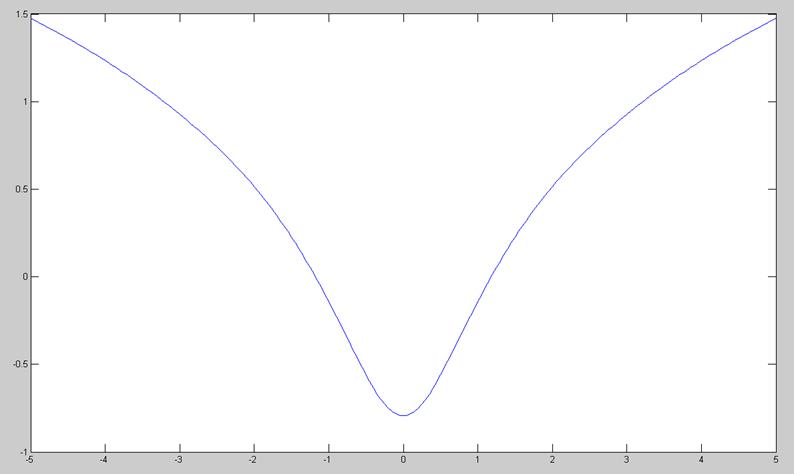
По этим графикам хорошо видно, что функция z(x, y) имеет 10 минимумов, которые расположены симметрично относительно мнимой оси, и не имеет минимумов на самой мнимой оси. Это подтверждает расчеты критерия дихотомии.