Вычисления в пакете Wolfram Mathematica 7.0. Решение переопределенной системы

Смирнов Д.Д., 6121

Вычисления проводились в пакете Wolfram Mathematica 7.0

Задание № 3. Пример 8. На отрезке [-1,1] измеряется сигнал f(x) в точках x_j. Погрешность сигнала не более d. Аппроксимировать экспериментальные данные полиномом

.

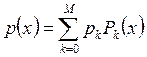Замечание: свести задачу к решению переопределенной системы

, где , - измеренные в точке x_jзначения функции f(x_j), .

Привести следующие данные: .

Данные задачи:

Решение:

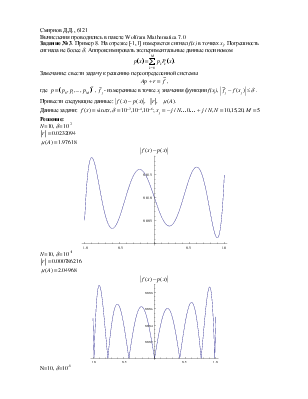
N=10, d=10^-2

0.0232094

1.97618

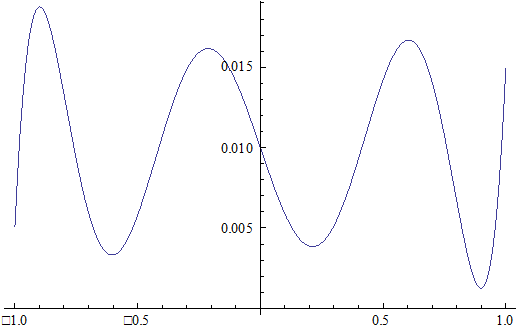
N=10, d=10^-4

0.000786216

2.04968

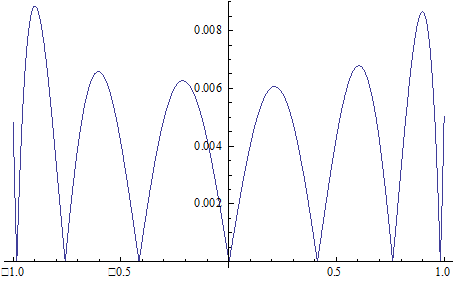
N=10, d=10^-6

0.0000152934

2.3474

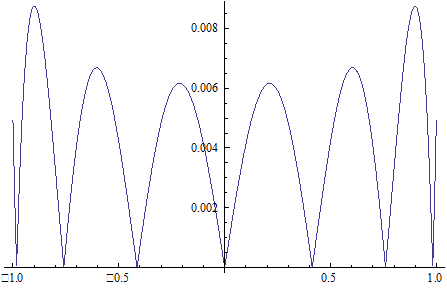
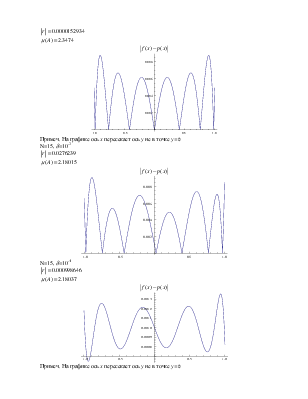
Примеч. На графике ось x пересекает ось y не в точке y=0

N=15, d=10^-2

0.0276239

2.18015

N=15, d=10^-4

0.000998646

2.18037

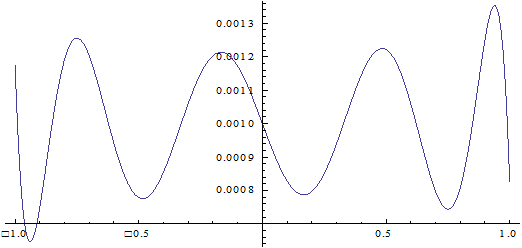
Примеч. На графике ось x пересекает ось y не в точке y=0

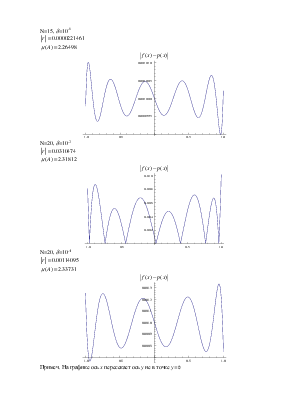
N=15, d=10^-6

0.0000221461

2.26498

N=20, d=10^-2

0.0310474

2.31812

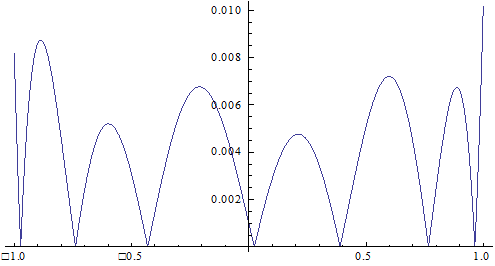
N=20, d=10^-4

0.00114095

2.33731

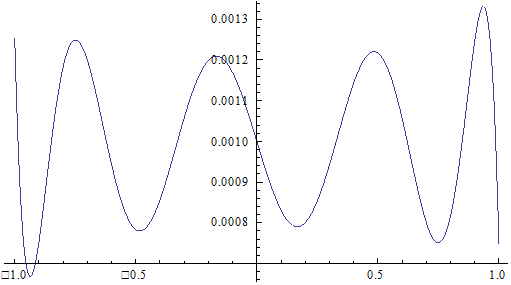
Примеч. На графике ось x пересекает ось y не в точке y=0

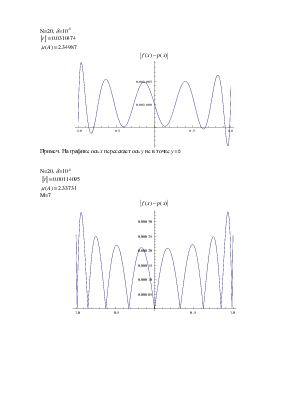
N=20, d=10^-6

0.0310474

2.34987

Примеч. На графике ось x пересекает ось y не в точке y=0

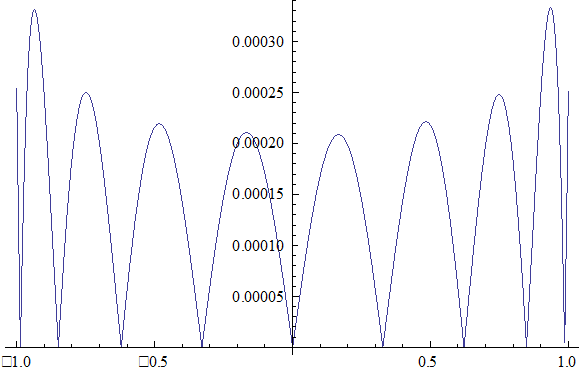
N=20, d=10^-6

0.00114095

2.33731

N=20, d=10^-6

0.0000262435

2.34987

M=9

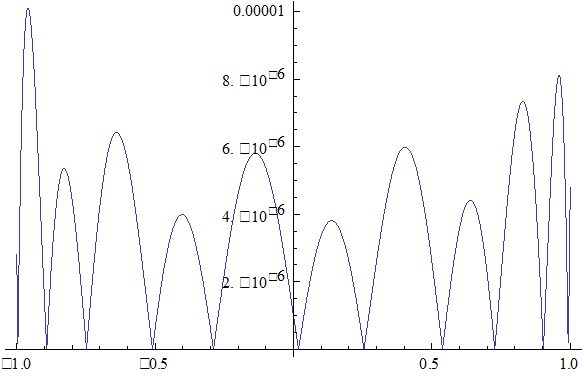Для того, чтобы уменьшить погрешность вычислений нужно увеличить количество полиномов (М). Рассмотрены случаи для М=7 и М=9 и эти случаи были сравнены с результатами, полученными при М=5. Из этих результатов можно заключить, что при вышеуказанном увеличении М погрешность вычислений уменьшается на порядок, но стремится к погрешности измерения, что иллюстрируют выше приведённые графики