

Relation of the Condensate Phase Transitions and
the Nucleation Rate Surface Singularities
Institute of Chemical Kinetics and Combustion, SB RAS, 3 Institutskaya Str., 630090 Novosibirsk, Russia
Abstract. The first order phase transitions in a condensed matter produce the nucleation rate surface singularities. That conclusion follows from the empirical results on nucleation of a vapor-gas systems. The singularity examples for nucleation rate surfaces in a vicinity of critical line conditions for several vapor-gas systems are presented. A nucleation surface singularity is a result of a molecule accommodation coefficient change of one phase to other one, as well as a gap in the first derivative of a chemical potential of a condensed phase and presumably a derivative gap in an excess energy of the critical embryos.
An advanced problem for nucleation experiments appears when the phase transition exists in a condensed state of matter. Such transitions produce the triple point on a diagram of phase equilibria. There could be a change in the dominant form of the forming embryo phase from one type such a liquid to a different phase such as a solid. The Gibbs free energy of the critical embryos governs the nucleation rate. It is easy to show that first derivative of nucleation rate surface needs to split when nucleation occurs in the vicinity of phase transition of the first order in a condensed phase.
|
|
|
0.
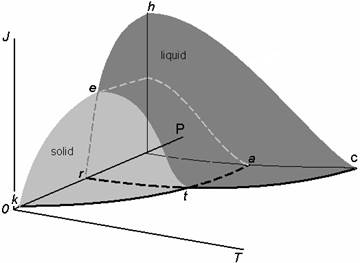
The topology of nucleation rate surfaces near a triple point is illustrated in Fig. 1 (Anisimova et al., 2001). It is plausible to think that nucleation rate surface arises from line of PT phase equilibria. Two lines for phase equilibria with vapor exist in the triple point vicinity. Nucleation rates for these conditions are presented schematically by nucleation rate surfaces, grey colour for solid and dark grey for liquid embryos respectively, where line, et, shows the equal nucleation rates for both phases. That line represents dynamic equilibria where a first derivative of a nucleation rate surface is broken.
Anisimov et al. (2000) have suggested using continuity and monotonic behavior in the data analysis to find the anomalies in the nucleation rate surfaces. This approach can be illustrated by defining the nucleation rate surface by the function, F(x1, x2, ..., xn), where x1, x2, ..., xn are independent variables such as pressure, temperature, etc. When function F has continuous partial derivatives, the surface described by the function F(x1 , x2 , . . . , xn), is continuous and monotonic. For condition F=constant, the function, F(x1 , x2 , . . . ,xn) has n-1 independent variables. For one independent variable and a continuous and monotonic surface, the full derivative of F with respect to x1 at F = constant and n=2 can be written as
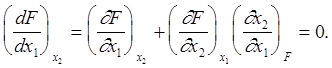 (1)
(1)
Subscripts show the constant values of variables as the conditions at which the derivative is evaluated. According to Anisimov et al. (2000), Eq. 1 can be rewritten as
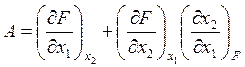 , (2)
, (2)
where A serves as a criterion for continuity and monotonic behavior. This criterion has nonzero values at any singular points in the surface F(x1, x2). The more general case for n variables is considered by Anisimov et al. (2000).
The nucleation rate with two variables, such as temperature, T, and vapor supersaturation, S, and constant values of all other parameters (P1...Pn) can be considered. It is customary to present the nucleation rate experimental results with the A-criterion. A simple relation can be obtained along the surface section where J(T,S) = constant:
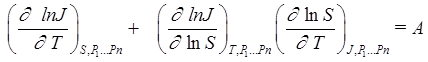 . (3)
. (3)
The criterion value, A, will be equal to zero if the vapor nucleation rate surface J = J(T,S) has no singularities. Because of experimental noise, the calculated values of A will include nonzero values that can be characterized by a non-dimensional standard deviation. The deviation of the A values from zero can characterize the quality of experimental results (if set of experimental values for J represent a continuous and monotonous surface). A singularity in the nucleation rate surface (or surface for any other set of experimental results) breaks the local condition for surface continuity and monotony. Fig. 2 presents the application of the A criterion for glycerin-carbon dioxide system. It can be seen that the A-criterion provides a sensitive tool for the detection of singularities in nucleation rate surfaces.
|
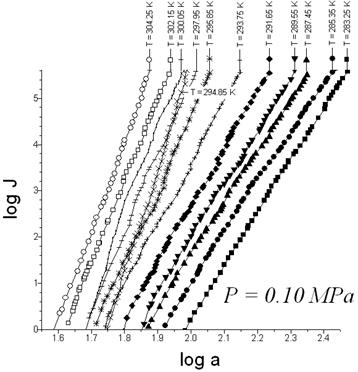
Fig. 3. The empirical nucleation rates (J) vs vapor activity (a) for the glycerin-carbon dioxide system.
The experimental data in Fig. 3 illustrate the presence of discontinuities for this system’s nucleation rate surface for a glycerine-carbon dioxide system. Discontinuity can be attributed to melting points of glycerin–carbon dioxide binary system. The melting temperature clearly increases with a rise in carbon dioxide pressure (P) from 0.1 to 0.2 MPa (Fig. 3). Presumably the carbon dioxide concentration in solution increases proportional to the total pressure.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.