Relation of the Condensate Phase Transitions and the Nucleation Rate Surface Singularities, страница 2

	Fig. 4. Glycerine vapor activity on nucleation      temperature.		Fig. 5. Schematic presentation of a chemical potentials, m, of vapor and condensed phases of 1 and 2 on a vapor activity in a vicinity of glycerine phase transition of the first order (p.t.).

 

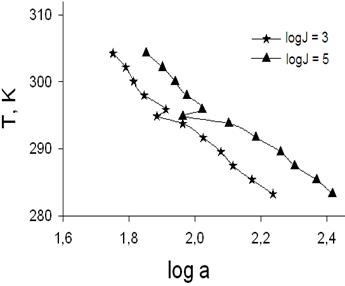
The glycerine vapor activities (a) on nucleation temperatures (T) for two levels of the nucleation rates (J) is shown in Fig. 4 for a total pressure 0.10 MPa. The same shapes are appeared for total pressure of 0.20 MPa. The clear discontinuities, which are produced by melting points, can be seen for all cases. 

                                                                                      

	Fig. 6. Two vapor-gas systems are illustrating a discontinuity gaps.  Gaps reveal two phase transitions in a condense solutions of carbon dioxide – diols which were unknown before.

 

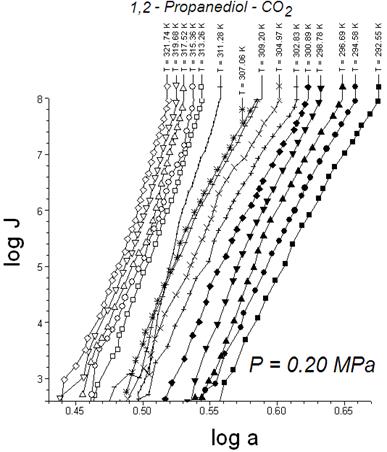
Let look the reasons for these discontinuities. In our experiments we have transition from a nucleation rate surface of one phase (J₁) to other one (J₂). In common case nucleation rates can be expressed such as J = B exp(-DG/kT).  In that equation DG = n*(m_cond -m_vapor) + f; where n* is number of molecules in the critical embryos; f is an excess energy of a critical embryo comparing with n* molecules in a bulk condensed phase (presumably df/dT has a discontinuity in the phase transition vicinity); Dm= m_cond -m_vapor is difference (shown schematically in Fig. 5) of the chemical potentials of the macro-scale samples of condensed phases and vapor respectively. Partial derivative dm_cond /dT is broken at conditions for a condensate phase transition of the first order; m_vapor is a continuous and monotonous function of temperature. The variable terms  dDm/dT and df/dT are negative and positive quantities respectively. In some cases a difference of partial derivatives (dDm/dT - df/dT) can be equal to zero and a nucleation rate surface has a local continuity and monotony. Local continuity conditions look like intersections of the nucleation isotherms such as in Fig. 3 or Fig. 6. These Figures show an impact of a critical embryo phase change on the nucleation rate surface topology.

A similar problem was found by Peeters et al. (2002).  However, the observed jump in the water vapor nucleation rates was not reproduced in the next report from that group (Holten et al., 2005).  It may be that there is sufficient experimental variation in the nucleation rate measurements which is preventing the detection of this kind of nucleation event. A major problem in detection of the nucleation rate surface singularities is the random error inherent in any experimental data.  This problem exists even one has experimental results of relatively high accuracy such as those of Strey et al. (1995) as it is shown by Anisimov et al. (2000).  In such circumstances, the conditions of continuity and monotony (Anisimov et al., 2000) of the nucleation rate surface can (should) be applied.

A conceptual problem in vapor-gas to liquid (or solid phase) nucleation is its treatment of the nucleation as a single component problem instead as a two component system. Results of the present research illustrate clearly that gases can generate a phase transitions in a condensed state of matter. It has led conclusion that gas can be involved in the critical embryos composition and any vapor-gas system nucleation should be considered in an approximation of binary solution. A direct mass spectrometric measurements show the presence of the carrier gas in the critical cluster under some nucleation conditions for example in a monosilane-argon system (Sharafutdinov et al., 1999).    

 Acknowledgements

Prof. P.K. Hopke is acknowledged for the useful and stimulating discussions of problem. The scientific community that is providing vapor-gas nucleation studies is acknowledged.    The present study was conducted under Basic Research Russian Foundation support through grant numbers of 07-08-13529-ofi and 07-03-00587-а. 

References

Anisimov, M.P.  Nasibulin, A.G., & Shandakov, S.D. (2000). Experimental detection of nucleation rate surface singularity. Journal of Chemical Physics, 112, 2348 – 2354.

Anisimova, L., Hopke, P.K., & Terry, J. (2001). The channel vapor nucleation in the vicinity of the triple point. Journal of Chemical Physics, 114, 9852 – 9855.

Holten, V., Labetski, D., & van Dongen, M.E. (2005). Homogeneous nucleation of water between 200 and 240 K: New wave tube data and estimation of the Tolman length. Journal of Chemical Physics, 123, 104505 – 104509.

Peeters, P., Gielis, J.J., & van Dongen, M.E. (2002). The nucleation behavior of supercooled water vapor in helium. Journal of Chemical Physics, 117, 5647 – 5253.

Sharafutdinov, R. G., Zarvin, A. E., Korobeyshchikov, N. G., Madirbaev, V. Zh., & Khmel, S. Ja. (1999). Clusters in a pulsed free jet of a monosilane-argon mixture. Technical Physics Letters, 25(21), 47 – 51.

Strey, R., Viisanen, Y., & Wagner, P.E. (1995). Measurement of the molecular content of binary nuclei. III. Use of the nucleation rate surfaces for the water-n-alcohol series. Journal of Chemical Physics, 103, 4333 – 4345.