Оптимальное закрепление за станками операций по обработке деталей. Усложненные задачи транспортного типа

Фирма переводит свой головной завод на производство определенного вида изделий, которые будут выпускаться в течение четырех месяцев. Величина спроса в течение этих четырех месяцев составляет 150,250, 230,350 изделий соответственно. В каждый месяц спрос можно удовлетворить за счет:

- запасов изделий, произведенных в прошлом месяце, сохраняющихся для реализации в будущем;

-производства изделий в течение текущего месяца;

-избытка производства изделий в более поздние месяцы в счет невыполненных заказов.

Затраты на одно изделие в каждом месяце составляют 5 д.е. Изделие, произведенное для более поздней реализации, влечет за собой дополнительные издержки на хранение в 2 д.е. в месяц. С другой стороны, каждое изделие, выпускаемое в счет невыполненных заказов, облагается штрафом в размере 1 д.е. в месяц. Объем производства изделий меняется от месяца к месяцу в зависимости от выпуска других изделий.

В рассматриваемые 4 месяца предполагается выпуск 100, 230, 330, 320 изделий соответственно. Требуется составить план, имеющий минимальную стоимость производства и хранения изделий.

Решение.1. Составим матрицу стоимости изделия из периода i в период j.

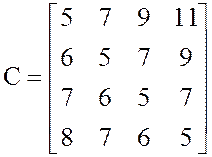, стоимость производства в i-й период, i = j;

стоимость производства в i-й период + стоимость задержки от где c_ij=         i до j, i < j;

стоимость производства в i-й период + штраф за нарушение срока, i > j;

при i = j, с₁₁ = с₂₂ = с₃₃ = с₄₄ = 5, т.е. затраты в период i при реализации продукции в тот же период оцениваются только стоимостью производств;

при i < j , т.е. если в период i производится продукция, которая будет потребляться позже , то имеют место дополнительные издержки, связанные с хранением, например с₂₅ = с₂₂ + 2 + 2 = 9; при i > j, т.е. производство в i-й период в счет невыполненных заказов влечет за собой дополнительные расходы в виде штрафа, например с₄₃ = с₃₃ + 1 = 5 + 1 = 6.

2.Составим таблицу задачи

3. Находим оптимальное решение

Х^* = (х₁₁=100, х₂₂ = 230, х₃₁ = 50, х₃₂ = 20, х₃₃ = 230, х₃₄ = 30, х₄₄ = 320).

4.Минимальная стоимость производства и хранения изделий min Z(X) = 5080.

7.4. задача о издании журналов

Имеется два сорта бумаги в количестве 15,10 т, которую можно использовать на издание трех журналов тиражом 17000, 13000, 10000 экземпляров. Расход бумаги на издание одного журнала составляет 0,7; 0,6; и 0,3 кг соответственно, а себестоимость тиража журнала при использовании i-го сорта бумаги задается следующей матрицей

.

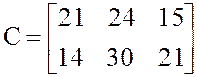Определить оптимальное распределение бумажных резервов.

Решение.1.Находим потребность в бумаге

2.Общие запасы бумаги составляют 15+10=25 т, а общие потребности – 11,9+7,8+3=22,7 т. Поэтому необходимо ввести фиктивный тираж

25-22,7=2,3 т с нулевыми затратами.

3.Преобразуем матрицу С относительно единицы бумаги (каждый столбец матрицы разделим на количество бумаги, приходящейся на один журнал).

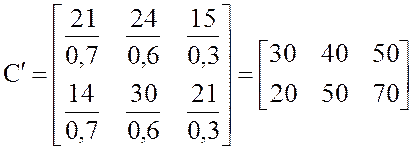
4.Составим таблицу задачи

5. Находим оптимальное решение min Z(X) = 719.

Бумага 1-го сорта в количестве х₁₁ = 1,9 т  затрачена на издание первого журнала, х₁₂ = 7,8 – на издание второго журнала, х₁₃ = 3 т – на издание третьего журнала, х₁₄ = 2,3 – не использовано. Бумаги 2-го сорта затрачено: на издание первого журнала в количестве х₂₁ = 10 т.

7.5. Задача о назначениях

Пусть имеется n различных работ и n различных лиц для выполнения этих работ. Известна производительность (с_ij) i-го лица при выполнении j-й работы. Необходимо определить, кого и на какую работу следует назначить, чтобы добиться максимальной суммарной производительности, при условии, что каждое лицо может быть назначено только на одну работу.

Решение. Обозначим через х_ij назначение i-го лица на j-ю работу.

Тогда, так как количество лиц равно количеству работ и каждое из них может быть назначено только на одну работу, х_ij принимает только два значения: единица, если i-е лицо назначается для выполнения