Задачи по теории графов. Основные понятия, задачи сетевого планирования

Тема I

Глава 1. Задачи по теории графов

Основные понятия.

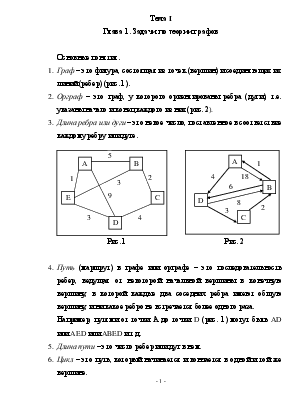
1.  Граф – это фигура, состоящая из точек (вершин) и соединяющих их линий (ребер) (рис. 1).

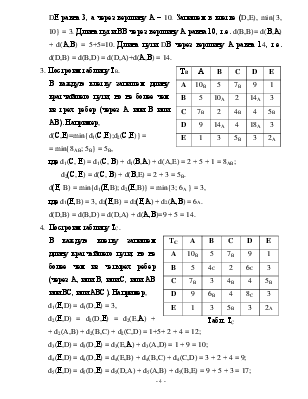
2.  Орграф – это граф, у которого ориентированы ребра (дуги), т.е. указаны начало и конец каждого из них (рис. 2).

3. 

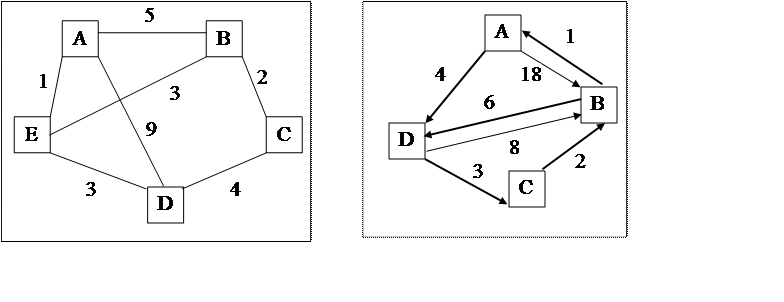Рис. 1                                                 Рис. 2

4.  Путь (маршрут) в графе или орграфе – это последовательность ребер, ведущая от некоторой начальной вершины в конечную вершину, в которой каждые два соседних ребра имеют общую вершину, и ни какое ребро не встречается более одного раза.

Например, путями от точки А до точки D (рис. 1) могут быть AD или AED или ABED и т.д.

5.  Длина пути – это число ребер или дуг в нем.

6.  Цикл – это путь, который начинается и кончается в одной и той же вершине.

7.  Граф или орграф называется связанным, если две любые его вершины можно соединить по крайней мере одним путем.

8.  Дерево – это путь без циклов.

Задача 1.

Найти кратчайший путь между всеми вершинами графа (см. рис. 1).

Табл. Т_1,2                                                    Табл. Т_3,4

1.  Заполним табл. Т_1,2 следующим образом.

Обозначим через d(x, y) длину пути от x до y. Диагональю будут являться точки А, В, С, D, E. Для них d(A,A)=d(B,B)=d(C,C)=d(D,D)= d(E,E)=0. Над диагональю запишем длины кратчайших путей, но не более чем из одного ребра (в противном случае поставим ∞).

Таким образом,

d(A,В) = 5, d(А,С) = ∞, d(А,D) = 9, d(A,E) = 1, d(B,C) = 2,

d(B,D) = ∞, d(B,E)= 3, d(C,D) = 4, d(C,E)= ∞, d(D,E) = 3.

Под диагональю запишем длины кратчайших путей, состоящих не более чем из двух ребер (иначе поставим ∞).

d₁(A,В) = 5, d₂(A,B) = d(A,E) + d(E,B) = 1 + 3 = 4,

d(A,В) = min{d₁(A,В); d₂(A,В)} = min{5;4} = 4_E.

d₁(A,C) = d(A,B) + d(B,C) = 5 + 2 = 7,

d₂(A,C) = d(A,D) + d(D,C) = 9 + 3 = 13,

d(A,C) = min{d₁(A,C); d₂(A,C)} = min{7;13} = 7_B.

Аналогично находим:

d(A,D) = 4_E, d(А,E) = 1, d(B,C) = 2, d(B,D) = 6_C или d(B,D) = 6_Е,

d(B,Е) = 3, d(С,D) = 4, d(С,E)= 5_В, d(D,E) = 3.

2.  Заполним табл. Т_3,4 следующим образом.

Над диагональю запишем длины кратчайших путей, но не более чем из трех ребер, а под диагональю - длины кратчайших путей, но не более чем из четырех ребер. Таким образом, под диагональю записаны кратчайшие пути между всеми вершинами графа.

Задача 2.

Найти кратчайшие пути между всеми вершинами графа (рис. 1) через транзитные вершины.

1.  Построим таблицу условий Т₁ следующим образом: запишем в диагональные клетки обозначения вершин A, B, C, D, E. Для них d(A,A)= d(B,B)=d(C,C)=d(D,D)=d(E,E)=0.

Над диагональю запишем длины кратчайших путей, но не более чем из одного ребра (в противном случае поставим ∞).

2.  Построим таблицу Т_А .

В каждую клетку запишем длину кратчайшего пути, но не более чем из двух ребер (через транзитную вершину А). Например, длина пути DЕ равна 3, а через вершину А – 10. Запишем в клетке (D,E), min{3, 10} = 3. Длина пути ВВ через вершину А равна 10, т.е. d(B,B)= d(В,А) + d(А,В) = 5+5=10. Длина пути DВ через вершину А равна 14, т.е. d(D,B) = d(B,D) = d(D,A)+d(А,В) = 14.

3.  Построим таблицу Т_В.

В каждую клетку запишем длину кратчайшего пути, но не более чем из трех ребер (через А или В или АВ). Например,

d(С,Е)=min{d₁(С,Е);d₂(С,Е)} =

= min{8_AB; 5_B} = 5_B, где d₁(С, Е) = d₁(С, В) + d₁(В,А) + d(A,E) = 2 + 5 + 1 = 8_AB;

d₂(С, Е) = d(С, В) + d(В,E) = 2 + 3 = 5_B.

d(Е, B) = min{d₁(Е,B); d₂(Е,B)} = min{3; 6_А } = 3, где d₁(Е,B) = 3, d₂(Е,B) = d₂(Е,А) + d₂(А,В) = 6_А.

d(D,B) = d(B,D) = d(D,A) + d(А,В)=9 + 5 = 14.

4.  Построим таблицу Т_С.

В каждую клетку запишем длину кратчайшего пути, но не более чем из четырех ребер (через А, или В, или С, или АВ или ВС, или АВС). Например,

d₁(Е,D) = d₁(D,Е) = 3,

d₂(Е,D) = d₂(D,Е) = d₂(E,А) + + d₂(A,B) + d₂(B,C) + d₂(C,D) = 1+5+ 2 + 4 = 12;

d₃(Е,D) = d₃(D,Е) = d₃(E,А) + d₃(A,D) = 1 + 9 = 10;

d₄(Е,D) = d₄(D,Е) = d₄(E,B) + d₄(B,C) + d₄(C,D) = 3 + 2 + 4 = 9;

d₅(Е,D) = d₅(D,Е) = d₅(D,A) + d₅(A,B) + d₅(B,E) = 9 + 5 + 3 = 17;

d(Е,D) = d(D,E) = min{3;12;10;9;17} = 3.

5.  Построить таблицу Т_D.

6.  Построим таблицу Т_Е.

В табл. Т_Е записаны кратчайшие пути между вершинами данного графа через транзитные вершины.

Например,

d(B,C) = d(B,D) + d(D,C) = 6 + 3 = = 9_D;

d(D,A) = d(D,B) + d(B,A) = 8 +1 = 9_B;

d(A,B) = min{d₁(A,B); d₂(A,B)} = min{18; 10} = 10, где d₁(A,B) = 18;

d₂(A,B) = d₂(A,D) + d₂(D,B) = 4 + 6 = 10_D.

Задача 3.

Найти кратчайшие пути между всеми вершинами графа (см. рис. 2).

1.  Построим таблицу Т₁.

Запишем в клетки диагонали метки вершин A, B, C, D. Для них d(A,A)=d(B,B)=d(C,C) = =d(D,D) =d(E,E)= ∞. Символ "∞" означает, что связь не существует. Над и под диагональю запишем длины кратчайших путей не более чем из одного ребра (в противном случае - ∞).

Например, d(A,D) = 4, d(D,А) = ∞, d(A,B) = 18, d(B,A) = 1.

2.  Построим таблицу Т₂.

Над и под диагональю запишем длины кратчайших путей не более чем из двух ребер (в противном случае - ∞).

3.  Построим таблицу Т₃.

Над и под диагональю запишем длины кратчайших путей не более чем из трех ребер.

Например, d₁(B,C) = d₁(B,A) + d₁(D,C) =

= 1+4+3 = 8_AD,

d₂(B,C) = d₂(B,D) + d₂(D,C) = 6 + 3 = 9;

d(B,C) = min{d₁(B,C); d₂(B,C)} =

min{8_AD; 9_D} = 8_AD.

Таким образом, в табл. Т₃ записаны кратчайшие пути между вершинами данного графа.

Задача 4.

Найти кратчайшие пути между всеми вершинами графа (рис. 2) через транзитные вершины.

1.  Построим таблицу условий Т.

Запишем в клетки диагонали метки вершин A, B, C, D. Для них d(A,A)=d(B,B)=d(C,C) = = d(D,D) =d(E,E)= ∞. Над и под диагональю запишем длины кратчайших путей не более чем из одного ребра (в противном случае - ∞).

Например, d(A,В) = 18, d(B,A) = 1, d(B,C) = ∞.

2.  Построим таблицу Т_A.

В каждую клетку запишем длину кратчайшего пути не более чем из двух ребер через транзитную вершину А. Например, длина пути BD через вершину А равна d₁(B,D) = d(В,А) + d(А,D) = 1+4=5_A,

d₂(B,D) = 6, d(B,D) = min {5;6} = 5_A.

d(B,B) = d(B,A) + d(A,B) = 1+18 = 19_A.

d(A,C) = ∞.

3.  Построим таблицу Т_В.

В каждую клетку запишем длину кратчайшего пути, но не более чем из трех ребер через транзитную вершину В (через А или В или АВ). Например,

d(С,A)=d(С,B) + d(B,A) = 2 + 1 = 3_B;

d₁(С,D) = d₁(С,В) + d₁(В,D) = 2 + 6 = 8_B;

d₂(С,D) = d₂(С,В) + d₂(В,A) + d₂(A,D) = 2 + 1 +4 = 7_BA;

d(C,D) = min{d₁(C,D);d₂(C,D)} = min{8_B;7_BA} = 7_BA;

d(A,A)=d(A,B) + d(B,A) = 18 + 1 = 19_B;

d(D,D)=d(D,B) + d(B,D) = 8 + 6 = 14_B;

d₁(A,D) = 4, d₂(A,D) = d₂(A,B) + d₂(B,D) = 18 + 6 = 24_B;

d(A,B) = min{4;24_B} = 4.

4.  Построим таблицу Т_С.

В каждую клетку запишем длину кратчайшего пути, но не более чем из четырех ребер через транзитную вершину С (через А, или В, или С, или АВ или СВ, или ВА и т.д.).

Например,

d₁(D,A) = d₁(D,B) + d₁(B,A) = 8 + 1 = 9_B;

d₂(D,A) = d₂(D,C) + d₂(C,B) + d₂(B,A) = = 3 + 2 + 1 = 6_CB;

d(D,A) = min{9,6} = 6_CB;

d₁(D,D) = d₁(D,B) + d₁(B,D) = 8 + 6 = 14_B;

d₂(D,D) = d₂(D,C) + d₂(C,B) + d₂(B,D) = 3 + 2 + 8 = 13_CB;

d₃(D,D) = d₃(C,D) + d₃(C,B) + d₃(B,A) + d₃(A,D) = 3 + 2 + 1 + 4 = 10_CBA;

d(D,D) = min{14;13;10} = 10.

5.  Построим таблицу Т_D.

В каждую клетку запишем длину кратчайшего пути, не более чем из пяти ребер (через А, или В, или С, или В; или АВ или ВA, или АВ, или DС и т.д.). Например,

d₁(A,A) = d₁(A,B) + d₁(B,A) = 18 + 1 = 19_B;

d₂(A,A) = d₂(A,C) + d₂(D,B) + d₂(B,A) = 4 + 8 + 1 = 13_DB;

d₃(A,A) = d₃(A,D) + d₃(D,C) + d₃(C,B) + d₃(B,A) = 4 + 3 + 2 + 1 = 10_DCB;

d(A,A) = min{19;13;10} = 10_DCB;

d(A,C) = d(A,D) + d(D,C) = 4 + 3 = 7_D.

Таким образом, в табл. Т_D записаны кратчайшие пути между вершинами данного графа через транзитные вершины.

Залача 5.

Найти кратчайшие пути между всеми вершинами графа (рис. 3).

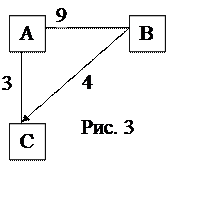1.  Построим таблицу условий Т₁. Запишем в клетки диагонали метки вершин A, B, C. Для них d(A,A)=d(B,B)=d(C,C) = ∞. Над и под диагональю запишем длины кратчайших путей не более чем из одного ребра (в противном случае поставим ∞).

Например, d(В,С) = 4, d(С,В) = ∞.

2.  Построим таблицу Т₂.

Над и под диагональю запишем длины кратчайших путей не более чем из двух ребер.

Например, d₁(B,А) = d₁(В,С) + d(С,А) = 4+3=7_С; d₂(B,А) = 9, d(B,А) = min{7_С;9} = 7_С;

d(С,B) = d(С,A) + d(A,B) = 3+9 = 12_A.

Задача 6.

Найти кратчайший путь между всеми вершинами графа (рис. 3) через транзитный вершины.

1.  Построим таблицу условий Т₁. Запишем в клетки диагонали метки вершин A, B, C. Для них d(A,A)=d(B,B)=d(C,C) = ∞. Над и под диагональю запишем длины кратчайших путей не более чем из одного ребра (в противном случае поставим ∞).

2.  Построим таблицу Т_А следующим образом:

В каждую клетку запишем длину кратчайшего пути не более чем из двух ребер через транзитную вершину А. Например, d(B,В) = =d(В,А)+d(А,В)=9+9=18_A, d₁(B,С)=d₁(B,A) + d₁(A,C) = 9 + 3 = 12_A,

d₂(B,C) = 4,

d(B,C) = min{12_A;4} = 4.

3.  Построим таблицу Т_B следующим образом:

В каждую клетку запишем длину кратчайшего пути не более чем из трех ребер через А или В; или АВ; или через ВА. Например, d(А,А) = d(А,В) + d(В,А) = 9+9=18_В.

4.  Построим таблицу Т_С.

В каждую клетку запишем длину кратчайшего пути через