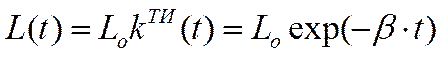Методы оценки динамики изменения и определения нормативных значений основных показателей технической эксплуатации автомобилей, страница 2

.                   (2.10)

Построим график зависимости (2.10) (см. рис. 2.2)

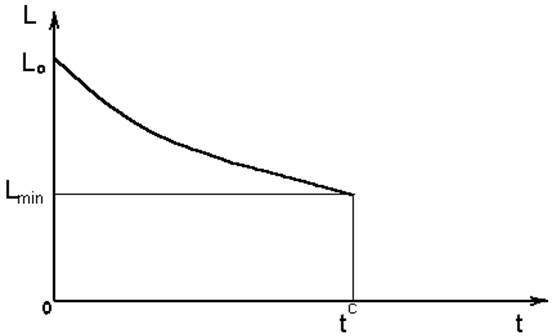Рис. 2.2 Изменение пробега автомобиля в процессе его эксплуатации.

Пробег автомобиля до списания (суммарный пробег автомобиля за весь период эксплуатации) на рис.2.2 численно определяется площадью, ограниченной осями координат и кривой .

Определим эту площадь:

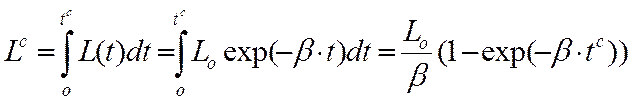,        (2.11)

с чётом (2.3) полученное выражение принимает вид

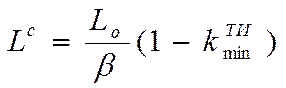.                          (2.12)

Среднемесячный пробег автомобиля за весь период его эксплуатации

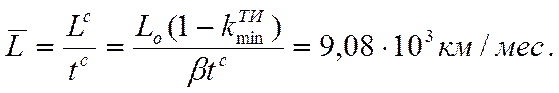,           (2.13)

А с учётом формул (2.7) и (2.8) это выражение принимает вид

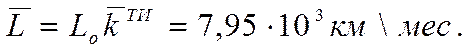.                        (2.14)

Определим среднемесячный пробег автомобиля перед его списанием:

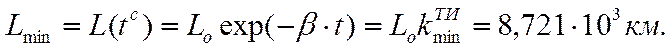        (2.15)

Находим, что за время эксплуатации месячный пробег автомобиля при списании в сравнении с месячным пробегом нового автомобиля уменьшается в µ раз:

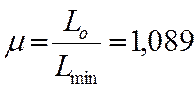
Коэффициент технического использования автомобиля при списании (в сравнении со значением этого коэффициента для нового автомобиля) также уменьшается в

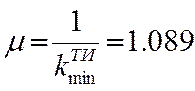                           (2.16)

Пусть автомобиль имеет возраст . Определим ожидаемый пробег этого автомобиля за период времени :  (2.17)

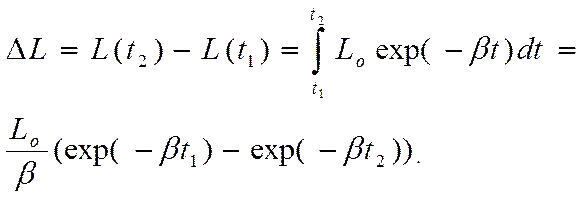         (2.17)

Формулы(2.12) – (2.17) имеют важное практическое значение, поскольку они могут использоваться при планировании пробега автомобиля, срока его эксплуатации, качества ТЭ, оценке потенциальных возможностей и уровня технического состояния парка автомобилей, управления возрастной структурой подвижного состава  и в целом ряде других случаев. Очевидно, что выражение (2.15) является наиболее общей формулой, связывающей ожидаемый пробег автомобиля с периодом его эксплуатации в зависимости от возраста автомобиля. В частности, при  и  имеем  и абсолютную тождественность формул (2.12) и (2.17).

Сравнивая формулы (2.13) и (2.14) легко заметить, что

,

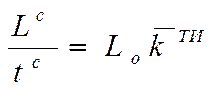откуда следует, что реализуемый коэффициент технического использования автомобиля за весь период его эксплуатации можно определять по формуле

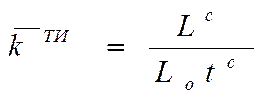.                             (2.18)

Из уравнения (2.14) видно, что для определения значения реализуемого коэффициента технического использования автомобиля можно использовать выражение

, которое связывает с  пробегом автомобиля.

Определим ожидаемый пробег нового автомобиля за период его эксплуатации , воспользовавшись для этой цели выражением (2.17)

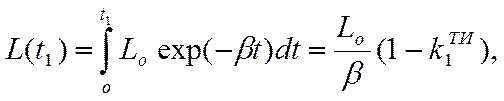            (2.19)

где  - ожидаемое значение коэффициента технического использования автомобиля в момент времени.

Рассмотрим параметр , определяемый по формуле

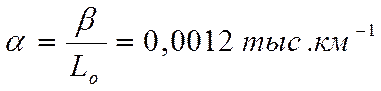.                                     (2.20)

Подставив уравнение (2.20) в формулу (2.19), получим

.                                (2.21)

Анализируя выражение (2.21), можно отметить экспоненциальный характер зависимости  пробега автомобиля  от времени эксплуатации .

Из уравнения (2.21) видно, что

                               (2.22)

В выражениях (2.21) и (2.22) присутствует параметр , определяемый по формуле (2.20), этот параметр оценивает количественное уменьшение коэффициента технического использования автомобиля за единицу его пробега.

Для рассматриваемого в примере АТП коэффициент технического использования автомобиля за каждые 1000 км пробега будет падать на 0,0012. Найдем по формуле (2,22) значение коэффициента использования автомобиля, совершившего пробег L = 300,0 • 10³ км:

II

III

Пробег автомобиля за четвертый год эксплуатации находим по формуле (2.17). Поскольку t₁ = 36 мес., а t₂ = 48 мес., то

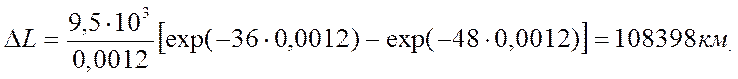
Пробег автомобиля за четыре года эксплуатации

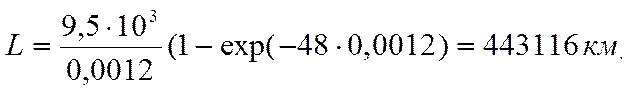
Среднемесячный пробег автомобиля за четвертый год эксплуатации

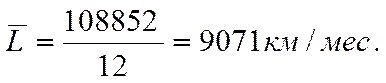
Среднемесячный пробег автомобиля за четыре года эксплуатации

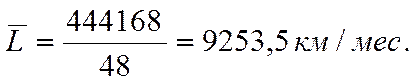
Коэффициент технического использования автомобиля к концу четвертого года эксплуатации

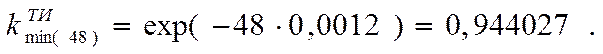
Реализуемый коэффициент технического использования за четвертый год эксплуатации

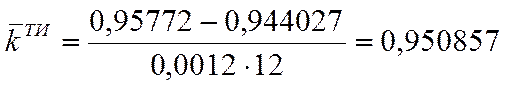, а значение этого коэффициента за четыре года эксплуатации:

 

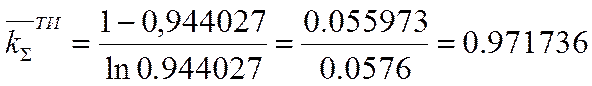
Аналогичным образом можно провести расчет показателей для каждого полугодового периода эксплуатации (табл.2.2).

Прогноз динамики показателей, характеризующих эксплуатацию автомобиля на АТП (табл.2.1).