Эффективная система слежения за задержкой. Оптимизация следящей системы

преобразование представляет собой функцию, аппроксимирующую натуральный логарифм, который является точным отображением z-плоскости на s-плоскость. При взятии преобразования Лапласа над дискретным сигналом (представляющего последовательность отсчётов), результатом является Z-преобразование с точностью до замены переменных:

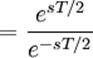
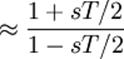                                   (10.1)       

Где   — период квантования (обратная к частоте дискретизации величина). Аппроксимация, приведённая выше и является билинейным преобразованием.

Суть метода  состоит в том, что непрерывные интегрирующие звенья, входящие в систему, заменяют дискретными интеграторами, осуществляющими интегрирование по методу трапеций.

Для определения характеристик следящей системы в переходном режиме воспользуемся дискретной передаточной функцией для ошибки, которая при использовании метода билинейного преобразования получается из передаточной функции замкнутой непрерывной системы  путем замены оператора непрерывного интегрирования:

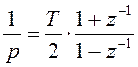,                                                (10.2)

где  - интервал дискретизации, выбираемый в соответствии с теоремой Котельникова из условия 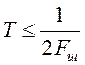 ( реально выбираем на порядок меньше, чтобы исключить накопление ошибок из-за округления чисел).

Полученную в результате дискретной аппроксимации (10.2) передаточную функцию цифровой модели необходимо представить в виде:

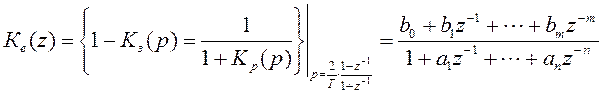.            (10.3)

Этой передаточной функции соответствует разностное уравнение:

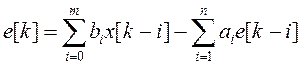.                                  (10.4)

Для исследуемой, системы передаточная функция замкнутой системы (3.6) равна:

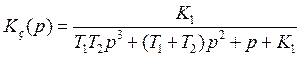 .                                    (3.6)

Тогда дискретная передаточная функция для ошибки будет равна:

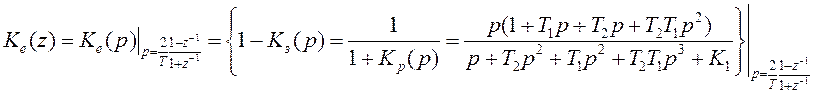(10.5

где  - шаг дискретизации, .

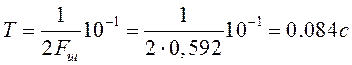Итак, делая замену 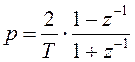, произведем преобразования:

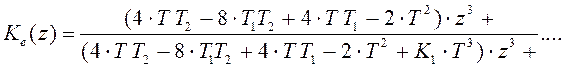
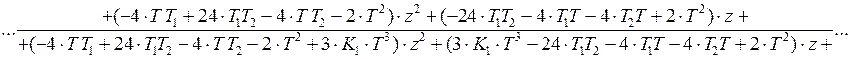
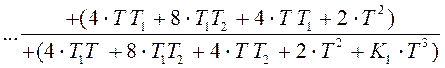,                         (10.6)

где   - добротность системы

Сравнивая с 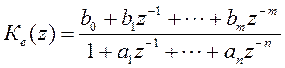, находим коэффициенты разностного уравнения:

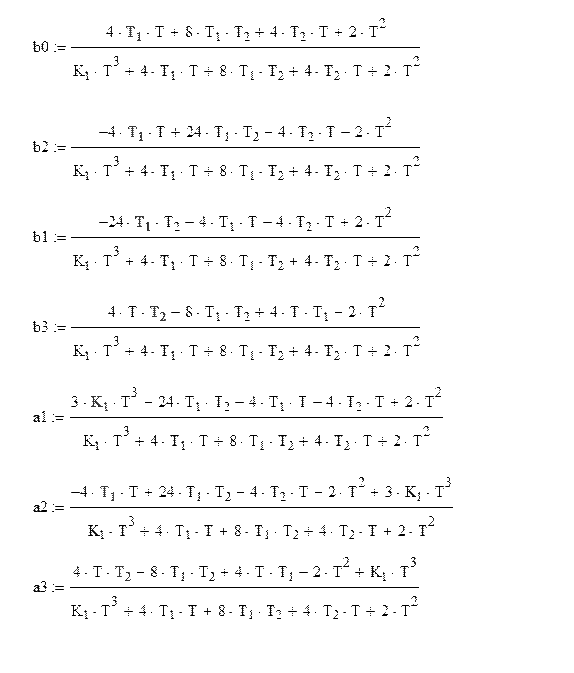
Этой передаточной функции соответствует разностное уравнение:

 (10.14)

где , , ,

, ,

Качественные показатели переходного процесса (быстродействие, перерегулирование) определяется по графику зависимости  ( - дискретное время кратное интервалу  дискретизации). Быстродействие оценивается временем переходного процесса  (время, в течение которого ошибка уменьшается по абсолютной величине до значения 0.01), а перерегулирование – величина максимального выброса  в переходной характеристике.

Построим отклик системы на единичное ступенчатое воздействие (, где )

Рисунок 9 – Единичное ступенчатое  воздействие

Рисунок 10 – Переходной процесс системы

Как видно из графика перерегулирование системы равно , а время переходного процесса (быстродействие) будет равно

Построим отклик системы на линейное воздействие (, )

Рисунок 11 – Линейное воздействие

Рисунок 12 – Переходной процесс в системе при линейном воздействии

Из графика видно, что характеристика стремится к значению 0,7591 мкс, которое соответствует динамической ошибке системы.

11.   Функциональная схема следящей системы

Данная система слежения за задержкой входит в состав  следящего измерителя дальности некогерентной импульсной РЛС (сложный ФМ сигнал), функциональная схема которого представлена на рисунок 13.

Рассмотрим его принцип действия. Зондирующий сигнал, который представляет из себя периодическую последовательность радиоимпульсов заданной формы с меняющейся по линейному закону частотой заполнения, отражаясь от цели, поступает в приемник РЛС, где усиливается, фильтруется от помех