



Федеральное агентство по образованию
Государственное общеобразовательное учреждение высшего профессионального образования
ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ
СИБИРСКОГО ФЕДЕРАЛЬНОГО УНИВЕРСИТЕТА
РАСЧЕТНО-ГРАФИЧЕСКОЕ
ЗАДАНИЕ
(Вариант №38)
Выполнил:
ст-т гр. Р 54-2
Проверил:
преподаватель
Красноярск 2007
1. ТИПОВЫЕ ЗВЕНЬЯ СИСТЕМ РАДИОАВТОМАТИКИ
Задача 1.17.
Построить график АФХ (годограф) звена, передаточная функция которого
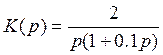
Решение:
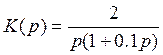
Разбиваем передаточную функцию на две составляющие.
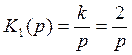 - передаточная функция интегрирующего
звена, где k=2
- передаточная функция интегрирующего
звена, где k=2
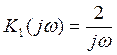
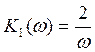 - АЧХ
- АЧХ 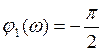 - ФЧХ
- ФЧХ
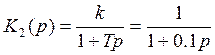 - передаточная функция инерционного звена,
где k=1, Т=0,1
- передаточная функция инерционного звена,
где k=1, Т=0,1
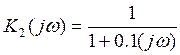
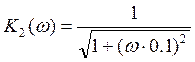 - АЧХ
- АЧХ ![]() - ФЧХ
- ФЧХ
Представим
передаточные функции в виде ![]()
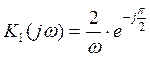
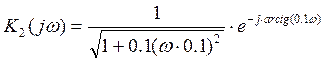
Для построения годографа необходимо вычислить значения АЧХ и ФЧХ передаточной функции при различных значениях частоты.
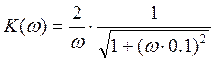
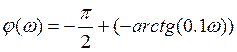
Составим таблицу:
|
ω |
0 |
2.5 |
5 |
7.5 |
10 |
12.5 |
15 |
17.5 |
20 |
30 |
40 |
∞ |
|
K(ω) |
∞ |
0.77 |
0.35 |
0.213 |
0.14 |
0.1 |
0.07 |
0.056 |
0.04 |
0.02 |
0.012 |
… |
|
φ(ω) |
-90 |
-104.03 |
-116.5 |
-126.8 |
-135 |
-141.3 |
-146.3 |
-150.2 |
-153.4 |
-161.5 |
-165.9 |
… |
2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ АВТОМАТИЧЕСКИХ СИСТЕМ
Задача 2.16. Для заданной структурной схемы
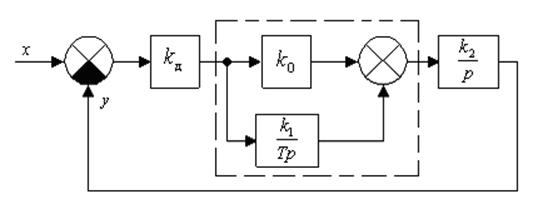
построить ЛАХ И ЛФХ разомкнутой системы, полагая kд=0,1; k0=10; k1=10; T=0,1с; k2=100 с-1.
Решение:
Выделим блок из типовых звеньев, образованный параллельным соединением безынерционного и интегрирующего звена, который описывается передаточной функцией:
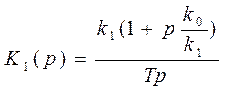
Тогда передаточная функция динамического звена будет иметь вид:
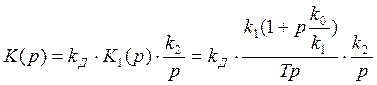
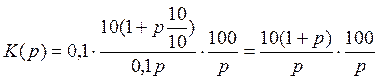
Разбиваем передаточную функцию на 3 составляющие:
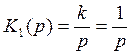 - передаточная функция интегрирующего
звена, где k=1
- передаточная функция интегрирующего
звена, где k=1
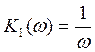 - АЧХ
- АЧХ 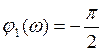 - ФЧХ
- ФЧХ
![]() - передаточная
функция форсирующего звена, где k=10, T=1
- передаточная
функция форсирующего звена, где k=10, T=1
![]() - АЧХ
- АЧХ ![]() - ФЧХ
- ФЧХ
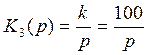 - передаточная функция интегрирующего
звена, где k=100
- передаточная функция интегрирующего
звена, где k=100
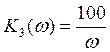 - АЧХ
- АЧХ 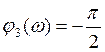 - ФЧХ
- ФЧХ
Тогда АЧХ и ФЧХ динамического звена:
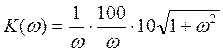
![]()
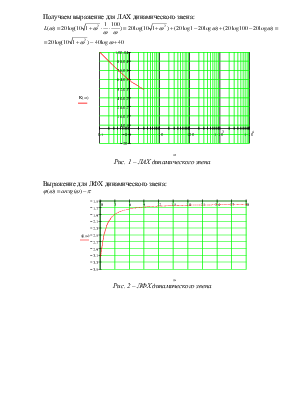
Получаем выражение для ЛАХ динамического звена:
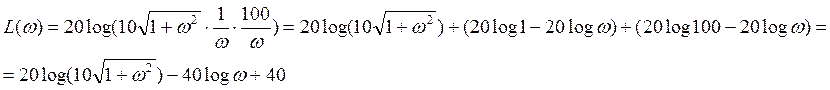
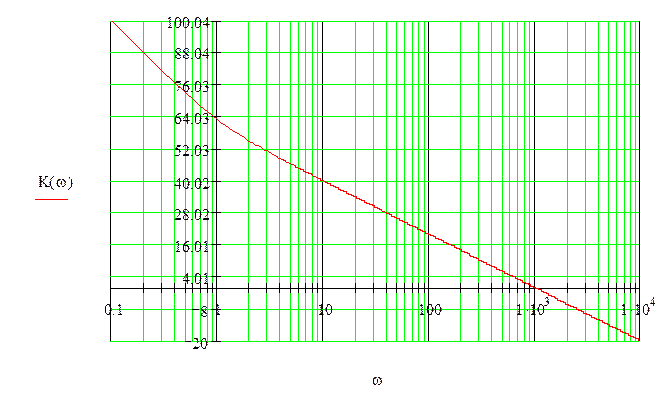
Рис. 1 – ЛАХ динамического звена
Выражение для ЛФХ динамического звена:
![]()
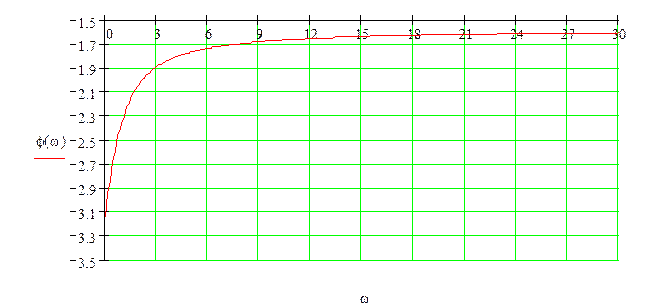
Рис. 2 – ЛФХ динамического звена
3. УСТОЙЧИВОСТЬ ЗАМКНУТЫХ АВТОМАТИЧЕСКИХ СИСТЕМ
Задача 3.15. ЛАХ разомкнутой системы имеет вид
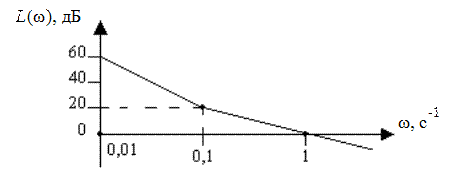
Определить запас устойчивости замкнутой системы.
Решение:
Анализируя ЛАХ, определяем количество типовых звеньев в разомкнутой системе:
k=3 - количество интегрирующих звеньев
m= 1- количество форсирующих звеньев.
Находим передаточную функцию разомкнутой системы:
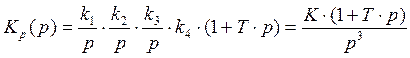 , где К – общее усиление разомкнутой системы.
, где К – общее усиление разомкнутой системы.
Тогда передаточная функция замкнутой системы определяется по формуле:
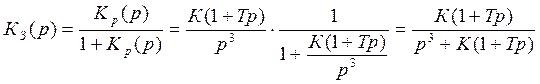
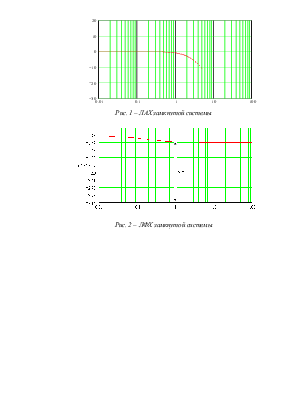
Построим кривую ЛАХ и ЛФХ для замкнутой системы:
![]()
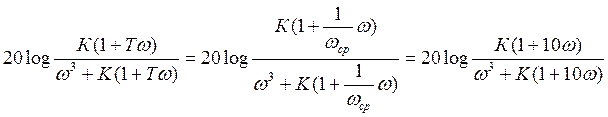
Если ЛФХ разомкнутой системы имеет вид:
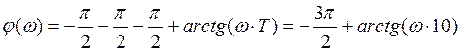
Значит ЛФХ замкнутой системы:
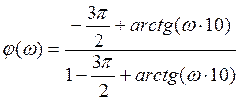
Если ЛФХ не пресекает горизонтальную прямую ![]() , то запас устойчивости определяется одним
показателем – запасом по фазе. Полученный запас устойчивости по фазе
удовлетворяет требованиям к запасу устойчивости АС:
, то запас устойчивости определяется одним
показателем – запасом по фазе. Полученный запас устойчивости по фазе
удовлетворяет требованиям к запасу устойчивости АС: 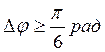 .
.
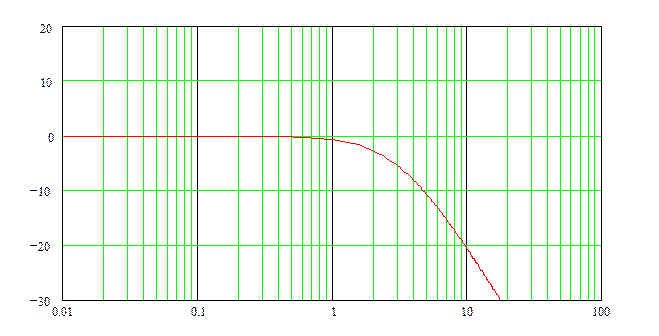
Рис. 1 – ЛАХ замкнутой системы
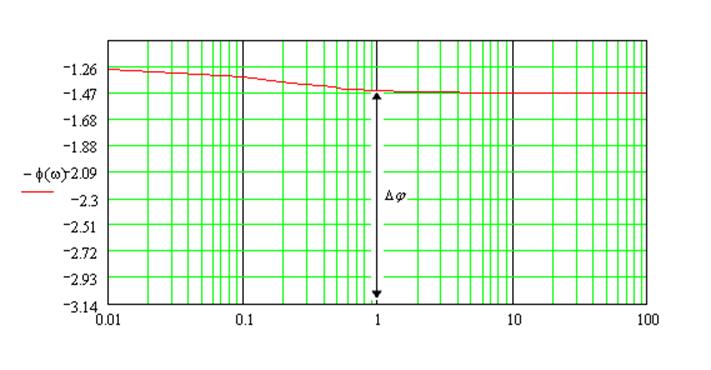
Рис. 2 – ЛФХ замкнутой системы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.