Область применения
К рупорным антеннам переходят для повышения направленности, КНД и улучшения согласования, т.к. волноводные излучатели имеют широкую ДН, малый КНД, плохо согласованы со свободным пространством. Поэтому особое применение они находят будучи использованными в качестве излучателей в направленных антеннах.
Выделяют несколько типов рупорных антенн.
Н - и Е - секториальные образованы путем плавного расширения пары противоположных стенок прямоугольного волновода.
Пирамидальный образованы путем плавного расширения всех стенок прямоугольного волновода.
Коробчатые образованы путем скачкообразного расширения стенок прямоугольного волновода. Они позволяют получить в небольшой полосе частот почти равномерное распределение поля Е и Н плоскостях.
Конические и биконические образованы путем плавного линейного расширения поперечного сечения круглых волноводов. Они позволяют получить игольчатые АДН с шириной главного лепестка 9-12 градусов.
Параметры и их расчет
Для нахождения поля излучения используется апертурный метод. Поле на внешней поверхности стенок рупора полагается равным нулю. Единственным критерием приемлемости апертурного метода является эксперимент.
С учетом цилиндрических координат напряженность электрического поля можно записать с точностью до множителя С:
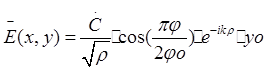, где 
- угол
раскрыва рупора, а зависимость амплитудного множителя от 
обусловлена цилиндричностью волны.
Согласно принятым выше допущениям выражение ;(5.10) оли-сывает электрическое поле и на раскрыве рассматриваемого рупора — отрезке соответствующего квазирегулярного волновода. Лз этого выражения, в частности, следует, что на любой малой
|
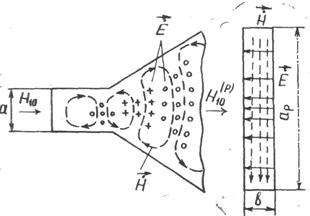
Преобразование плоской волны в цилиндрическую в H-плоскостном секториальном рупоре |
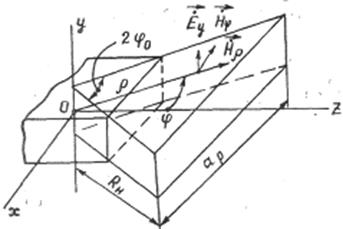
Цилиндрическая система координат, связанная
с H-плоскостным секториальным рупором площадке раскрыва рупора поле имеет одну и ту же ориентацию. Таким образом, к рупорному излучателю применима теорема перемножения (2.74), причем элементом излучения является источник Гюйгенса, а множитель системы может быть определен путем преобразования Фурье от амплитудно-фазового распределения (5ЛО).
Для расчета множителя системы лерейдем в выражении от цилиндрических координат ρ, φ к прямоугольным х, у в плос-кости, раскрыва. Тогда с учетом рис.3 можно записать:
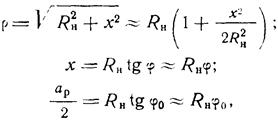
откуда) φ/φo=2x/ар. При записи этих соотношений учтено, что угол раскрыва рупора 2φ0 мал, т. е. ap/Rн<1, где ар и Rн — соответственно ширина и длина рупора.
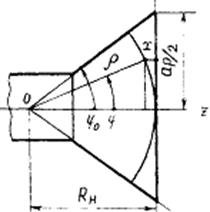
Рис 3 Связь цилиндрических и
прямоугольных координат на рас-
крыве рупора
Учитывая приведенные соотношения, формулу можно переписать в виде
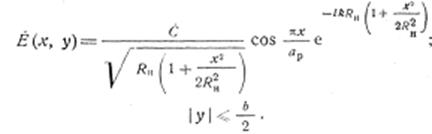
Воспользовавшись этим соотношением, определим, как это было сделано в случае волноводных излучателей, амплитудно-фазовое распределение тока в ЭЛА, ориентированных в главных плоскостях излучающего раскрыва. Проинтегрировав выражение по у, найдем амплитудно-фазовое распределение тока в ЭЛА, расположенной вH-плоскости (то оси х):
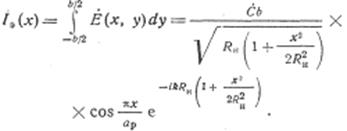
Из этого соотношения видно, что ЭЛА в H-плоскости не является синфазной. Фаза тока (без учета фазы комплексного множителя С)
распределена по квадратичному закону (рис.
4). Амплитуда тока спадает по закону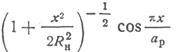
(рис. 4, сплошная линия), близкому к
косинусоидальному (штриховая линия), если Rн>aр. В E-плоскости
амплитудно-фазовое распределение тока в ЭЛА определим, проинтегрировав соотношение по х. Очевидно, что ЭЛА, ориентированная вдоль оси у и
имеющая длину b, будет
синфазной с .равномерным амплитудным распределением тока Iэ(y).
Установленный характер амплитудно-фазового распределения тока в ЭЛА позволяет рассчитать сечения множителя системы главными плоскостями. Так, в E-плоскости множитель системы будет совпадать с выражением ( ). В H-плоскости множитель
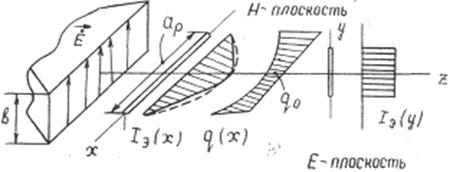Рис. 4. Амплитудно-фазовое распределение тока в ЭЛА, соответствующих H-плоскостному секториальному рупору
системы будет близок к формуле ( ) лишь для рупоров с малым углом раскрыва 2фо≈ар/Rн, когда максимальная квадратичная фазовая ошибка qmax = ka2/4Rн невелика. Изменение угла раскрыва 2φ0 сложным образом влияет на вид множителя систе мы в H-плоскости и его параметры. С одной стороны, увеличение угла 2φо, что эквивалентно росту ар при неизменном Rн, приводит к возрастанию волновых размеров эквивалентной линейной тенны и, следовательно, должно сопровождаться сужением глав ного лепестка множителя системы. С другой стороны, увеличение
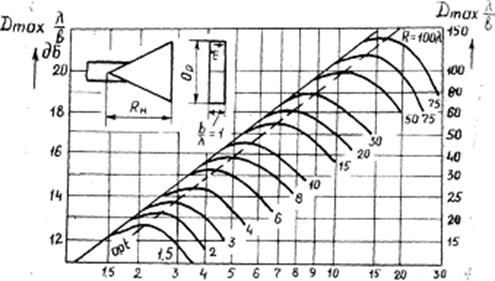
Рис.5 . Зависимость Dтяхот размеров H-плоскостного секториального рупора
2φо (или ар) приводит к росту квадратичной фазовой ошибки, что сопровождается расширением главного лепестка и возрастанием уровня боковых. Из этого следует, что зависимость максимального КНД от величины ар имеет экстремальный характер: при ap=ap opt величина Dmах достигает наибольшего значения. Оптимальная ширина рупора ар opt,, равно как и наибольшее значение Dmах, зависит от длины рупора Ra. На рис. 5 приведены графики зависимости Dmах от ар и Ra, рассчитанные для случая b/λ=1. Если у рупора иное значение b/λ, тс величину Dmax*λ/b найденную из графика, нужно умножить на фактическое значение b/λ. Расчеты показывают, что связь apopt с Rн определяется соотношением
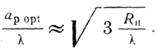
Аналогичным образом можно определить характеристики рупоров других типов.
Из-за спадающих амплитудных распределений в рупорах с линейным расширением размеров поперечного сечения не удается получить высокий КИП (даже при оптимально выбранных размерах ξ=0,5 ... 0,65). Этот недостаток преодолевается в коробчатых рупорах. Практически равномерное амплитудное распределение на раскрыве коробчатого рупора удается обеспечить за счет возбуждения в нем многоволнового режима. Рассмотрим, например, коробчатый рупор, образованный скачкообразным расширением прямоугольного волновода в H-плоскости. В
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
