Необходимо обработать большой массив экспериментальных данных, состоящий из равноточных значений отсчета

измерений подчиняются нормальному закону распределения вероятности.

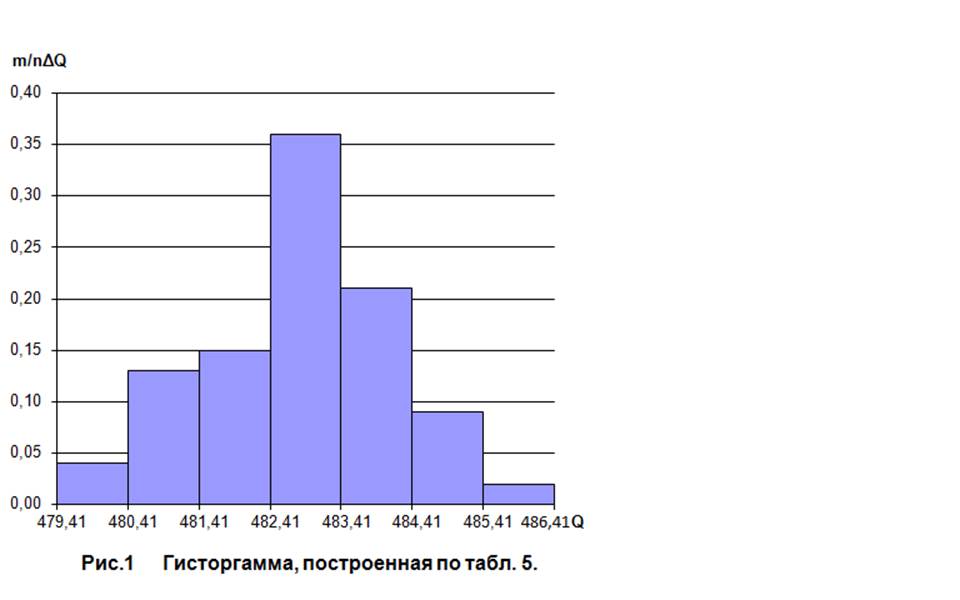
3. Проверим гипотезу о соответствии экспериментальных данных нормальному закону распределения вероятности с помощью критерия К. Пирсона. Сведем все полученные значения в таблицу 6.

3.1  При использовании критерия К. Пирсона  χ² за меру расхождения экспериментальных данных с теоретическим законом распределения вероятности принимается сумма квадратов отклонения частей m_i/n от теоретической вероятности P_i попадания отдельного значения результата измерения в i-й интервал, причем каждое слагаемое берется с весовым коэффициентом n/P_i:

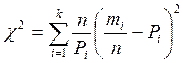
3.2  Определим, на сколько S_Q и в каком направлении отстоит от среднего арифметического правая граница Q_i каждого интервала:

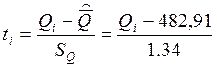
Полученные значения параметра t_i внесем в четвертую графу табл.6

3.3  Функцию Лапласа L(t_i) , берем из прил.1 и заносим в пятую графу табл.6

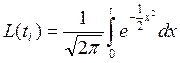
Таблица 6.

3.4  Теоретическая вероятность P_i попадания в i-й интервал отдельного значения результата измерения, подчиняется нормальному закону,

P_i = L(t_i) - L(t_i-1)

Принимая во внимание, что L(-∞)= -0,5, а L(+∞)= 0,5, поместим рассчитанные значения P_i в шестую графу табл.6.

3.5 В седьмую и восьмую графу внесены результаты остальных вспомогательных вычислений. Суммирование чисел в восьмой графе дает

χ²=0,159

По графику интегральной функции распределения вероятности К. Пирсона (рис.70):

χ² < χ²₀

Исходя из этого, принимаем гипотезу о том, что результат измерения подчиняется нормальному закону распределения вероятности.

4. Гипотеза о нормальности закона распределения вероятности результата измерения не противоречит экспериментальным данным.

4.1 Определим стандартное отклонение среднего арифметического :

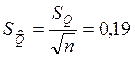
4.2 Выберем доверительную вероятность P=0,95

По рисунку 52 определим t=2,0

4.3 Рассчитаем половину доверительного интервала:

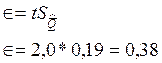
4.4 Запишем результат решения задачи в форме указания интервала, в котором находится числовое значение измеренной физической величины с вероятностью 0,95.

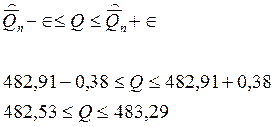
Ответ: интервал [482,53 ; 483,29] в котором находится числовое значение измеренной физической величины Q с выбранной вероятностью равной 0,95

Задача №2.

Необходимо обработать две сравнительно небольшие серии измерений.

Массив экспериментальных данных:

1 серия измерений

2 серия измерений

Для 1 серии измерений

1.  Исходя из того, что в подавляющем большинстве случаев результат измерения подчиняется нормальному закону распределения вероятности, исключим по правилу трех сигм ошибки, если они есть:

1.1.    Находим среднее арифметическое значение результата 1 серии измерений :  

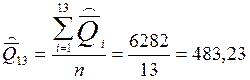
1.2.   Находим стандартное отклонение результата 1 серии измерений  S_Q, используя вычисления из табл.1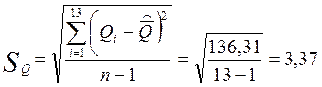   

1.3.    По правилу 3σ находим ошибки: 

-3σ_Q ≤ Q_i ≤ +3σ_Q

483,23-(3*3,37) ≤ Q_i ≤ 483,23+(3*3,37)

473,12≤ Q_i ≤ 493,34

Поскольку все результаты 1 серии измерений находятся в интервале      [473,12…493,34], можно считать, что все ошибки исключены

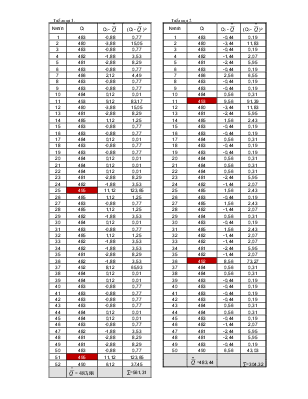
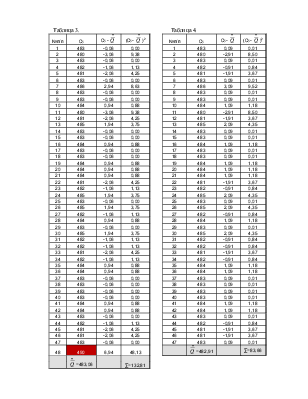
Таблица 1                                                                            

2. Проверим с помощью составного критерия справедливость сделанного допущения.

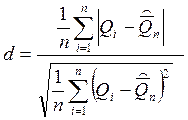
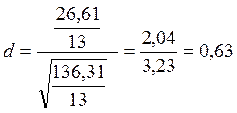
Проверяем выполнение условия

Не соблюдение данного условия достаточно для того, чтобы гипотеза о нормальности закона распределения вероятности результата измерения была отвергнута.

Для 2 серии измерений

1.  Исходя из того, что в подавляющем большинстве случаев результат измерения подчиняется нормальному закону распределения вероятности, исключим по правилу трех сигм ошибки, если они есть:

1.1. Находим среднее арифметическое значение результата 2 серии измерений :  

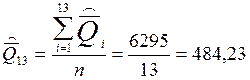
1.2.   Находим стандартное отклонение результата 2 серии измерений  S_Q, используя вычисления из табл.2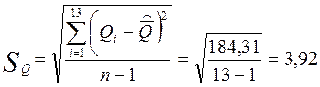   

1.3.    По правилу 3σ находим ошибки: 

-3σ_Q ≤ Q_i ≤ +3σ_Q

484,23-(3*3,92) ≤ Q_i ≤ 484,23+(3*3,92)

472,47 ≤ Q_i ≤ 495,99

Таблица 2                                                                

Поскольку все результаты 2 серии измерений находятся в интервале