Разработка структуры математических моделей солнечной фотоэлектрической системы энергоснабжения (буферная структура), страница 2

Первоначально проектируемые СЭС имели относительную низкую выходную мощность и малый ресурс. Они строились по буферной схеме параллельного соединения первичного источника, накопителя и нагрузки (рис.1). После того, как были исчерпаны ресурсы повышения эффективности таких систем за счет улучшения массоэнергетических характеристик источников электроэнергии, возникла необходимость в изменении буферной структуры и применении в системах электроснабжения электронных регуляторов и зарядно-разрядных устройств.

2 Декомпозиция для 3-х уровней (агрегатов, узлов, элементов)

На рис. 2 изображена схема декомпозиции СЭС на агрегаты, узлы и элементы. В дальнейшем она будет использована для построения математических моделей.

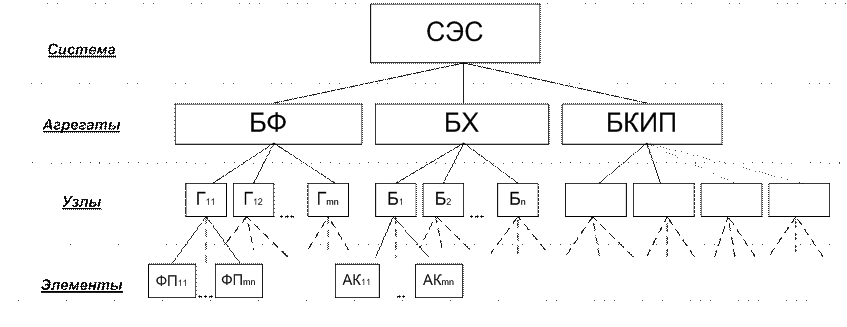Рис. 2. Схема декомпозиции буферной СЭС на агрегаты, узлы и элементы.

3 Разработка структуры функциональных связей (элементов СЭС)

Используя структурную схему и схему декомпозиции СЭС разрабатываем структуру функциональных связей на уровне элементов СЭС (см. рис. 3, 4). Декомпозиция связей элементов производится в предположении, что все АК и ФЭ по своим параметрам идентичны.

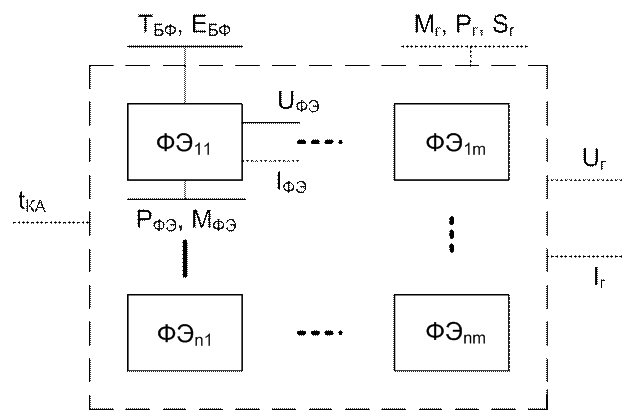
Рис. 3. Структура функциональных связей элементов БФ

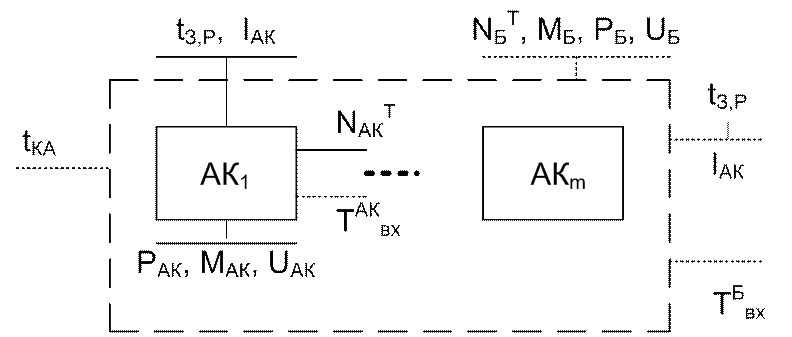
Рис. 4. Структура функциональных связей элементов БХ

Использованы следующие обозначения:

U_г – напряжение группы ФП;

I_г – ток группы ФП;

M_г – масса группы ФП;

Pг – вероятность безотказной работы группы ФП;

U_ФЭ, I_ФЭ, M_ФЭ, P_ФЭ – – напряжение, ток, масса, вероятность безотказной работы фотоэлектрических элементов;

Pг – вероятность безотказной работы группы ФП;

S_г – площадь группы ФП;

T_БФ – температура БФ;

E_БФ – освещенность БФ;

t_КА – время эксплуатации космического аппарата; аналогично обозначены параметры,  характеризующие БХ;

t_з,р – время заряда/разряда аккумуляторной батареи.

4 Разработка структуры математической модели СЭС с целью определения основных массовых, электрических, тепловых, надёжностных и др. характеристик агрегатов и СЭС в целом.

Математи́ческая моде́ль — это упрощенное описание реальности с помощью математических понятий. Используя математический аппарат, мы занимаемся математическим моделированием: заменяем реальный объект его моделью и затем изучаем последнюю. Как и в случае любого моделирования, математическая модель не описывает полностью изучаемое явление, и вопросы о применимости полученных таким образом результатов являются весьма содержательными.

Итак, для проектирования солнечной батареи СЭС КА будем применять математические модели СБ различной информативности. При разработке математической модели внешние связи системы с задачами, выполняемыми КА, заменяются их обобщенными количественными характеристиками.

Записшем математическую модель СЭС в виде следующих выражений. Основу модели составляют функциональные зависимости, внешние связи которых требуют конкретизации в каждом отдельном случае.

1.  Модель внешних факторов:

E_БФ = f(h_α, h_π, i, ψ, θ, Ω, П _со^БФ);

Т_БФ = f(h_α, h_π, i, ψ, θ, Ω, П _со^БФ);

Τ_об = f(h_α, h_π);

Т^вх_СЭС = f(N^Т_СЭС)

2.  Модель БФ:

M^ФЭ_уд = f(тип ФЭ);

M_ФЭ = M^ФЭ_уд∙S_ФЭ;

M_г = M_ФЭ∙m_ФЭ∙n_ФЭ;

M_БФ = M_г∙ m_г∙n_г∙k^БФ_кон;

k^БФ_кон = f(S_БФ);

S_г = S_ФЭ∙m_ФЭ∙n_ФЭ;

S_БФ = S_г∙ m_г∙n_г∙k_зап;

k_зап  = f(S_г, m_г, n_г);

P_ФЭ = f(τ_КА, тип ФЭ);

P_г = f(P_ФЭ, m_ФЭ, n_ФЭ);

P_БФ = f(P_г, m_г, n_г);

U_ФЭ = (U_БФ∙β^г_U∙ β^ФЭ_U)/ (n_г∙n_ФЭ);

β^г_U = f(n_г); β^ФЭ_U=f(n_ФЭ);

I_ФЭ = f(τ_КА, E_БФ, Т_БФ, U_ФЭ);

I_г = I_ФЭ∙m_ФЭ∙β^г_I;

I_БФ = I_г∙m_г∙β^БФ_I∙k_дегр;

β^г_I  = f(m_ФЭ); β^БФ_I=f(m_г);

k_дегр = f(τ_КА, тип ФЭ, h_α, h_π, α);

3.  Модель БХ:

M_АК = f(Q^max_АК, тип АК);

M_Б = M_АК∙n_АК∙k^Б_кон;

k^Б_кон = f(M_АК, n_АК);

M_БХ = M_Б∙n_Б∙k^БХ_кон;

k^БХ_кон= f(M_Б, n_Б);

P_АК = f(τ_КА, Q^max_АК, тип АК)

P_Б = P_АК∙n_АК;

P_БХ = P_Б∙n_Б;

N^T_АК = f(τ_КА, I_АК, τ_з(р), T^АК_вх);

I_АК = I_Б = I_БХ\ n_Б;

N^Т_Б = N^Т_АК∙n_АК;

N^Т_БХ = N^Т_Б∙n_Б;

U_АК = f(τ_КА, I_АК, τ_з(р), T^АК_вх);

Q^max_АК = f(I_БХ, U_БХ, τ_КА, T^БХ_вх, Q_доп);

U_Б = U_АК∙ n_АК;

U_БХ = U_Б;

4.  Модель БКИП:

M_БКИП =f(τ_КА, T^БКИП_вх, I_БФ, I_БА, U_БА, τ_БА);

P_БКИП = f(τ_КА, T^БКИП_вх, I_БФ, I_БА, U_БХ, U_БА, τ_БА);

N^T_БКИП =f(τ_КА, T^БКИП_вх, I_БФ, I_БА, U_БА, τ_БА);

I_БХ = f(τ_КА, T^БКИП_вх, I_БФ, I_БА, U_БХ, U_БА, τ_БА);

τ_з(р) = f(τ_КА, T^БКИП_вх, I_БФ, I_БА, U_БХ, U_БА, τ_БА);

U_БФ = f(U_БА)

5.  Для СЭС в целом:

M_СЭС = (M_БФ+M_БХ+M_БКИП+M_{каб.сети}) ∙k^СЭС_кон;

k^БФ_кон = f(M_БФ, M_БХ, M_БКИП);

P_СЭС = P_БФ∙P_БХ∙P_БКИП;

N^T_СЭС = N^T_БКИП + N^Т_БХ