Вопрос №52
Газовый цикл Брайтона. Оптимизированные расчеты по выбору параметров.
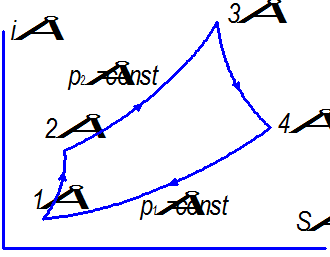
i0 – S0 – диаграмма цикла Брайтона.
Мощность газа, Вт, высвобождаемая в цикле Брайтона: Nц= Nт +Nк, где Nт – мощность газа, высвобождаемая в процессе расширения в турбине или МГД-генераторе;
Nк – мощность, затрачиваемая на сжатие газа в механическом или МГД-компрессоре.
Разность этих мощностей представляет собой полезную мощность, высвобождаемую в цикле, которую можно преобразовать в механическую или электрическую энергию.
В диаграмме i0 – S0:
10-20 – процесс сжатия реального газа в компрессоре, он протекает с ростом энтропии S0, так как наблюдается диссипация механической энергии газа при его трении и переход этой энергии в тепло; 20-30 – процесс нагрева газа в теплообменнике при Р20=const. Энтропия газа растет из-за его нагрева при контакте с первичным источником энергии (термохимический, ядерный, радиоизотопный реакторы, солнечный концентратор и коллектор);
30-40 – процесс расширения газа без теплообмена с внешней средой в турбине или в МГД-генераторе. Энтропия растет из-за диссоциации механической энергии при трении газа и перехода этой энергии в тепло;
40-10 – процесс охлаждения газа в холодильнике. В случае космической установки это холодильник-излучатель. Энтропия S падает из-за отвода тепла.
Если N=G∙L0, где G – массовый расход газа, кг/с; L0 – удельная работа газа, Дж/кг; Nт=Gт∙Lт0 – мощность турбины, Вт; Nк=Gк∙Lк0 – мощность компрессора, Вт, то эффективная мощность цикла равна:
Nц= Gт∙Lт0-Gк∙Lк0.
Если пренебречь расходом сжатого газа на собственные нужды энергоустановки и считать Gт=Gк=G, то эффективная работа цикла Брайтона:
Lц0= Lт0- Lк0, Дж/кг.
В космических условиях используют газотурбинные ЭУ, работающие по замкнутому циклу.
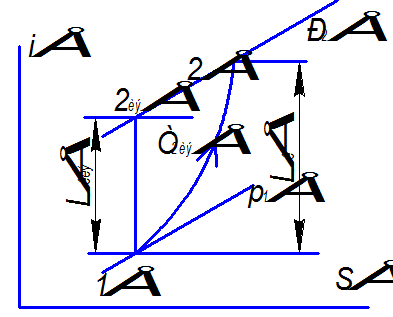
Процесс сжатия в компрессоре
10-20 – адиабатный процесс сжатия газа в компрессоре без теплообмена с окружающей средой, но при наличии диссипации энергии из-за трения реального газа;
10-2иэ0 – изоэнтропный процесс сжатия реального газа без теплообмена и диссипации энергии.
Удельная работа сжатия
реального газа, Дж/кг: ![]() .
.
Удельная работа сжатия
идеального газа, Дж/кг: ![]() .
.
Эти работы связанны через адиабатный КПД компрессора:
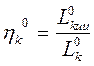 ,
, 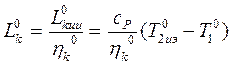 .
.
Вынося Т10
за скобки, получаем: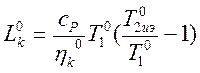 .
.
Связав температуры и давления
с помощью уравнения изоэнтропы 10-2иэ0,
находим: 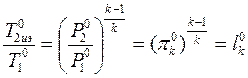 , где
, где 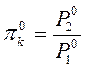 -степень
сжатия компрессора.
-степень
сжатия компрессора.
Тогда 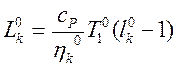 .
.
Аналогично можно найти работу расширения газа в турбине.
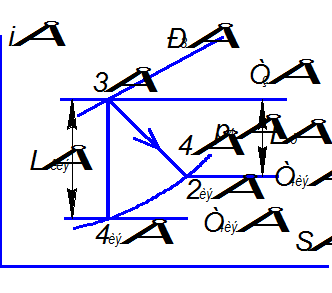
Для реального газа: ![]() , где
, где ![]() -
теплоемкость при постоянном давлении горячего газа в турбине.
-
теплоемкость при постоянном давлении горячего газа в турбине.
В случае расширения
идеального газа в турбине удельная работа расширения вдоль изоэнтропы 30-4иэ0:
![]()
Величины Lт0 и Lтиэ0 связанны величиной адиабатного КПД турбины:
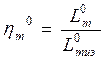 ,
,![]() .Вынося Т30 за
скобки, получаем:
.Вынося Т30 за
скобки, получаем:
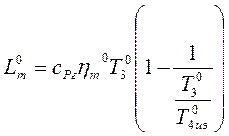 . Связав температуры и давления с помощью
уравнения изоэнтропы 30-4иэ0, находим:
. Связав температуры и давления с помощью
уравнения изоэнтропы 30-4иэ0, находим: 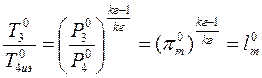 , где
, где
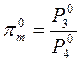 - степень расширения турбины,
- степень расширения турбины, 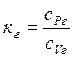 - показатель изоэнтропы горячего газа в
турбине.
- показатель изоэнтропы горячего газа в
турбине.
Тогда 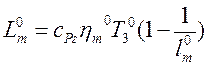 .
.
Эффективная работа цикла Брайтона:
Lц0= Lт0- Lк0=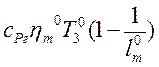
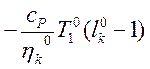 .
.
Связь степени расширения
турбины и степени сжатия компрессора: ![]() ,
, 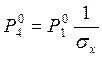 , где
, где ![]() и
и ![]() - коэффициенты восстановления полного
давления в подогревателе и холодильнике.
- коэффициенты восстановления полного
давления в подогревателе и холодильнике.
Тогда 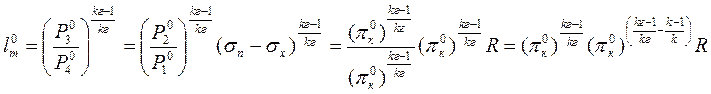 .
.
Опыт расчетов показывает, что
в большинстве случаев величина![]() ,
, ![]() .
.
![]() , где
, где ![]() - величина, характеризующая гидравлическое
сопротивление в контуре турбокомпрессора.
- величина, характеризующая гидравлическое
сопротивление в контуре турбокомпрессора.
Учитывая вышеизложенное можно записать:
Lц0= 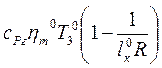
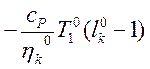 .
.
Вынося удельную работу сжатия
компрессора за скобки, получаем:
Lц0= 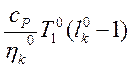
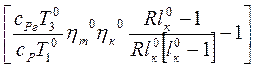 .
.
Введя обозначения 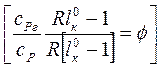 ,
, 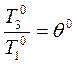 -
степень подогрева газа в цикле.
-
степень подогрева газа в цикле.
Находим Lц0= 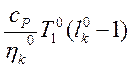
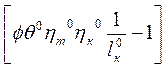 .
.
Величина ![]() характеризует гидравлические сопротивления
в контуре турбокомпрессора и изменение теплоемкости газа с ростом его
температуры.
характеризует гидравлические сопротивления
в контуре турбокомпрессора и изменение теплоемкости газа с ростом его
температуры.
Видно, что Lц0 зависит
от степени подогрева газа в цикле ![]() и его сжатия
и его сжатия ![]() . Величины
. Величины ![]() при
изменении параметров цикла изменяются слабо.
при
изменении параметров цикла изменяются слабо.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.