Материалы лекций № 1.8-9.
Модели линейных САУ.
******
Общая модель линейной непрерывной и дискретной САУ. Решение системы линейных дифференциальных уравнений с переменными коэффициентами. Краевые задачи. Линейные САУ, описываемые обыкновенными дифференциальными уравнениями с постоянными коэффициентами (Передаточная функция линейной САУ. Переходная функция. Весовая, или импульсная переходная, функция системы. Частотные и логарифмические характеристики линейной САУ.). Дискретные линейные САУ. Системы с цифровыми вычислительными машинами.
*****
Линейные САУ занимают особое место в теории автоматического управления. Обусловлено это двумя причинами.
Во-первых, очень многие реальные системы при некоторых ограничениях могут быть линеаризованы. Правда, методы линеаризации не всегда столь просты.
Во-вторых, методы решения линейных дифференциальных или разностных уравнений, которыми в данном случае описываются объекты управления – область давно разработанная.
Формализованным определением понятия линейности в приложении к математической модели объекта управления является требование линейности функций F(X, U, t) и N(X, U, t). Функция f(X1, Х2, ..., Хn) называется линейной, если выполнены условия:
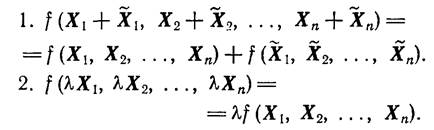(1.8-9.1. – 1.8-9.2.)
1.8-9.1. Общая модель линейной непрерывной и дискретной САУ
Требования линейности (1.8-9.1. – 1.8-9.1.) приводят к описанию (моделированию) объекта управления в виде:
(1.8-9.3.)
для непрерывных САУ и, соответственно,
(1.8-9.4.)
или
(1.8-9.5.)
для дискретных САУ. Будем, как и раньше, считать возмущения малыми (ξ<<1) т.е. будем считать ξ = 0, и работать с уравнениями
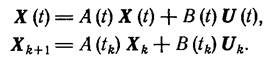(1.8-9.6. - 1.8-9.7.)
Характерной чертой линейных САУ, является возможность применения к ним принципа суперпозиции, который может быть сформулирован следующим образом. Пусть Uj(t) (j = 1, 2, ... , k) - некоторые, вообще говоря, различные, выбранные нами управления, а Xj(t) —соответствующие этим уравнениям траектории объекта управления в фазовом пространстве. Тогда для линейной САУ траектория движения объекта управления X(t) при действии управления
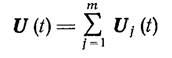(1.8-9.8.)
будет
равна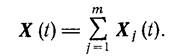 
(1.8-9.9.).
Этот принцип позволяет исследователю рассматривать результат действия каждого управления в отдельности, независимо от действия других управлений.
Очень часто линейные САУ описывают линейным дифференциальным уравнением вида:
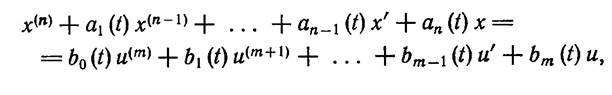(1.8-9.10.)
т. е. в несколько иной форме, чем (1.8-9.6.). Однако, по сути дела, описание (1.8-9.10.) эквивалентно описанию (1.8-9.6.) с точностью до обозначений. Введем следующие обозначения:
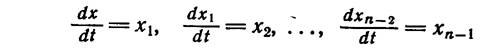(1.8-9.11.)
и, соответственно,
(1.8-9.12.)
тогда, рассматривая n-мерный вектор Х(t) = {х (t), x1(t), ..., xn(t)} и m + 1-мерный вектор U(t) ={u(t), u1(t), ..., un(t)} (считаем m + 1 < n, что обычно выполняется в реальных САУ), а также определив матрицу А размерности n × n как
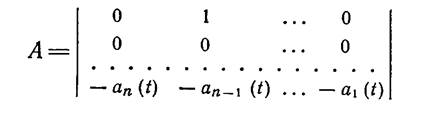(1.8-9.13.)
и матрицу В размерности n × (m + 1) равной
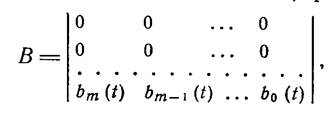(1.8-9.14.)
получим
(1.8-9.15.)
Таким образом, уравнение (1.8-9.10.)и система (1.8-9.6. - 1.8-9.7.) эквивалентны между собой. Каждому решению xi = хi(t) уравнения (1.8-9.10.) соответствует решение X(t) = {хi(t), хi1(t), ..., хi(n-1) (t)} системы (1.8-9.6. - 1.8-9.7.), и наоборот, каждому решению
(1.8-9.16.)
системы (1.8-9.6. - 1.8-9.7.) соответствует решение x(t) = xi(t) уравнения (1.8-9.10.), причем это соответствие однозначно.
Замечание. Из общей теории обыкновенных
дифференциальных уравнений в предположении, что элементы матрицы A(t) = {aij(t)}
и свободные члены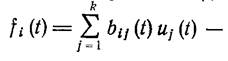 
непрерывные
функции на интервале (0, τ), следует, что система (1.8-9.6. - 1.8-9.7.)
при любых начальных условиях
(1.8-9.17.)
имеет решение на этом интервале, причем это решение единственное. Часто начальное условие (1.8-9.17.) записывают в виде
(1.8-9.18.)
где Х0— некий постоянный n-мерный вектор.
Аналогично для уравнения (1.8-9.10.)в предположении, что
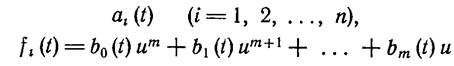(1.8-9.19. – 1.8-9.20.)
— непрерывные функции на интервале (0, τ), следует, что уравнение (1.8-9.10.)при любых начальных условиях
(1.8-9.21.)
имеет решение на этом интервале, причем это решение единственное.
Эти утверждения следуют из одной из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными) — задачи Коши. Простейшая задача Коши состоит в том, что требуется найти определенную на полупрямой t ≥ t0 вектор-функцию X(t), которая удовлетворяет уравнению
(1.8-9.22.)
и при t = t0 - принимает значение Х0, т. е. X(t0) = Х0. Коши в начале прошлого века доказал, что в предположении непрерывности f(X, t) для всех t и непрерывной дифференцируемости по Х эта задача всегда имеет решение, причем решение единственное и непрерывно зависящее от начальных данных.
1.8-9.2. Решение системы линейных дифференциальных уравнений с переменными коэффициентами.
Будем рассматривать нормальную систему линейных дифференциальных уравнений с переменными коэффициентами
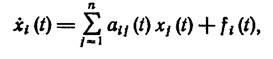(1.8-9.23.)
или, в векторной записи,
(1.8-9.24.)
В первую очередь исследуем однородную систему, т. е. случай f(t) ≡ 0(fi(t) ≡ 0, i=1,2, ..., n). Для однородной системы имеем
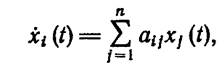(1.8-9.25.)
или, в векторной записи,
(1.8-9.26.)
Установим простейшие свойства этих уравнений.
1. Если X(t) = X0(t) — решение уравнения (1.8-9.26.) — обращается в нуль при некотором значении t0:
(1.8-9.27.)
то это решение тождественно равно нулю X0(t) ≡ 0, t0 < t < tk Такое решение называется тривиальным. Это свойство непосредственно следует из замечания изложенного
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
