В тесной связи с устойчивостью находится чувствительность характеристик системы к изменению параметров схемы, обусловленному, например, колебаниями температуры окружающей среды или старением параметров схемы.
Согласно закону Ома сопротивление R определяется отношением напряжения U к току I, при этом U — падение напряжения на сопротивлении, а I — протекающий через него ток. Аналогично можно определять отрицательное сопротивление
(2.6-7.9.)
При этом изменяется только знак. Таким образом, отрицательное отношение напряжения и тока определяет отрицательное сопротивление RОТ. С математической точки зрения уравнение (2.6-7.9.) очень просто. Однако с физической точки зрения последствия появления отрицательного знака гораздо значительнее, чем это может показаться на первый взгляд. Это подтверждают некоторые приведенные далее принципиальные соображения, касающиеся проблемы отрицательных сопротивлений.
Если представить цепь, состоящую из источника напряжения Uг и двух соединенных последовательно сопротивлений одинаковой величины, но с разными знаками (RОТ., RОТ.= — Rr.), то общее сопротивление этой цепи равно нулю (см. рисунок 2.6-7.14.). Таким образом, отрицательное сопротивление может компенсировать положительное сопротивление такой же величины. Однако это справедливо только отчасти, так как в этом случае получается цепь с общим сопротивлением исчезающе малой величины, при анализе которой возникают логические трудности. Ток I в цепи при любом небольшом напряжении источника Uг →0 принимал бы сколь угодно большое значение Iг →∞. Это противоречит здравому смыслу и практике. Поэтому линейное соотношение (2.6-7.9.) может быть справедливо только на некотором конечном участке вольтамперной характеристики; практически любая кривая, характеризующая отрицательное сопротивление в большом диапазоне амплитуд, должна быть нелинейной. Однако ограничение области линейности не разрешает полностью всех проблем. Так, в цепи с эквивалентной схемой, приведенной на рисунке 2.6-7.14. подведенный ток кратковременного действия не будет затухать во времени и в любой момент времени должен оставаться неизменным. Физическое истолкование уравнения (2.6-7.9.) позволяет привести еще и другие соображения. Знак минус у отношения напряжения к току может получиться двояким образом: изменением полярности напряжения или изменением направления тока:
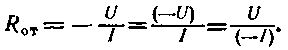(2.6-7.10.)
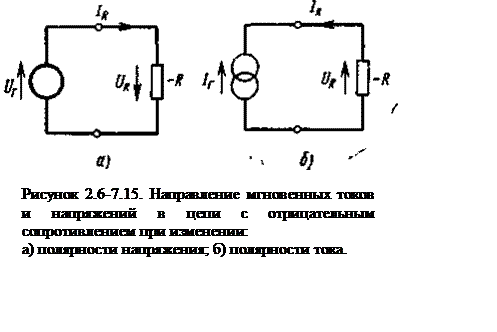
На рисунке 2.6-7.15. наглядно показаны соответствующие мгновенные полярность напряжения и направление тока. Очевидно, что отрицательные сопротивления одинаковой величины могут быть получены двумя разными способами: во-первых, изменением полярности напряжения; во-вторых, изменением направления тока.
С физической точки зрения разные причины возникновения отрицательных сопротивлений могут быть связаны также с различными режимами работы одной и той же схемы. Уже эти простые предварительные соображения показывают, что при анализе схем с отрицательными сопротивлениями нужно быть очень внимательным, чтобы избежать неожиданностей и ошибок.
2.6-7.5. Энергетический баланс цепи с отрицательным сопротивлением.
Анализ энергетических соотношений позволяет выявить дополнительные особенности отрицательных сопротивлений. На рисунке 2.6-7.16 для сравнения изображены две простые цепи с одним положительным (рисунок 2.6-7.16.а), а также с одним положительным и одним отрицательным сопротивлениями (рисунок 2.6-7.16.б). Определим мощность, потребляемую сопротивлением нагрузки RH (напряжение источника Ur, сопротивление нагрузки и отрицательное сопротивления заданы).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.