Переместив начало вектора в рабочую точку, где, как мы считаем, должно работать наше устройство, посмотрим как поведет себя годограф относительно этой точки. Он может описывать достаточно причудливую n-мерную траекторию, то, приближаясь то удаляясь от точки отсчета, но если с течением времени годограф не выходит за пределы некоторой n-мерной сферы радиуса Rуст то режим который мы выбрали для устройства устойчив. Rуст выбирается так, что бы перейдя эту границу устройству уже было проще перейти в другое состояние и т.д. Это один из подходов теории устойчивости.
Из вышеизложенного понятно, что для устойчивости системы даже динамическая ВАХ не будет представлять собой какую-то единственно возможную пусть и n-мерную линию, это будет область в фазовом пространстве, где для рассматриваемого устройства будут реализовываться, так сказать, виртуальные ВАХ не повторяющие друг друга. Эти ВАХ будут собственно реализациями, усреднение которых по какому-то правилу обязательно даст нам реальную статическую ВАХ. Но при одном условии. Каждая точка этой характеристики должна характеризовать устойчивый режим, т.е. такой режим в который обязательно устройство возвращается после окончания действия возмущений.
Для дальнейшего рассмотрения нам потребуется окончить “разбирательство” с внутренним сопротивлением устройства. Как следует из того, о чем говорилось раньше Rвн или Zвн отражает связь между напряжением и током двухполюсника, т.е. каждой точке статической ВАХ соответствует свое значение Rвн. Поэтому его называют статическим внутренним сопротивлением Rст. Поскольку выражение «статическое, внутреннее сопротивление» достаточно длинно то слово «внутреннее» обычно опускают. Остается: статическое сопротивление. О том какая информация в этой величине заключена уже говорилось выше, но, к сожалению, это сопротивление не отражает характера ВАХ, т.е. не несет информации о направлении изменения зависимости. Как исправить этот недостаток в общем-то понятно, необходимо взять не сами значения U и I, а их изменение т.е.:
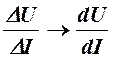. (2.6-7.9.)
Отсюда возникает понятие дифференциального или динамического сопротивления двухполюсника. В этой величине характер изменения зависимости указывается знаком: + если зависимость возрастающая, - если падающая. Но можно поступить иначе – брать производную не от напряжения по току, а от статического сопротивления по току. Знак в этом случае, так же как и выше укажет на характер зависимости.
На что указывает знак + в указанных выше производных, в общем-то, понятно: это увеличение напряжения на устройстве и тока через него, а, следовательно, и мощности вкладываемой в устройство. Но как уже отмечалось, при рассмотрении ВАХ газового разряда на них имеются участки, где дифференциальное сопротивление отрицательное.
2.6-7.4. Понятие отрицательного сопротивления, его смысл и особенности.
Электрические двухполюсники обычно имеют возрастающие вольтамперные характеристики, во всех точках которых дифференциальное сопротивление R=dU/dI положительно. Наряду с этим существуют также системы с падающими участками вольтамперной характеристики, т. е. с отрицательным дифференциальным сопротивлением (RОТР=dU/dI<0). В этом случае говорят о наличии отрицательных сопротивлений или в общем случае отрицательных импедансов.
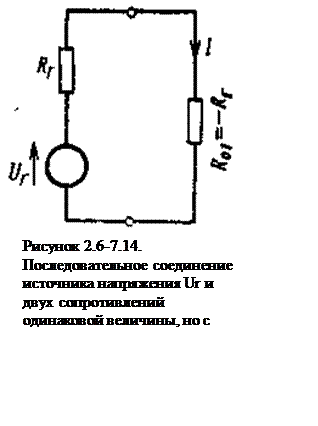Вольтамперная характеристика элементов
с отрицательными импедансами в широком диапазоне амплитуд в принципе нелинейна;
исходя из закона сохранения энергии, ясно, что она может иметь только
ограниченную падающую область. Если рабочая точка лежит на падающем участке
характеристики, то элемент при достаточно малых изменениях управляющей величины
можно рассматривать как линейный; при этом с отрицательным сопротивлением
допустимо (с учетом знака) оперировать как с положительным. Однако при анализе
схемы с отрицательными импедансами возникают некоторые характерные особенности,
которые не проявляются при анализе схем с положительными импедансами. Здесь на
первом месте стоит вопрос об устойчивости схем.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.