Испытания на действие ускорений и невесомости

Материалы лекции № 2.3.

Испытания на действие ускорений и невесомости.

*****

Виды ускорений, возможности их проявления и воспроизведения в условиях испытаний. Оборудование для проведения испытаний на воздействие линейных ускорений (Классификация центрифуг. Основными параметрами, характеризующие центрифуги. Основные типы центрифуг. Возможности обеспечения работы испытываемых объектов в ходе их испытаний на центрифуге.). Средства измерения линейных ускорений. Приборы для измерения частоты вращения. Методы испытаний на воздействие линейного ускорения. Испытания на воздействие невесомости (Невесомость и отказы технических устройств. Имитация условий воздействия динамической невесомости. Испытания по выявлению воздействия невесомости на функционирование технических систем и их компонентов.).

*****

2.3.1.Виды ускорений, возможности их проявления и воспроизведения в условиях испытаний.

При движении наземных транспортных средств, в летательных аппаратах, во вращающихся деталях механизмов, в ракетах и снарядах, во всех движущихся объектах возникают линейные и угловые ускорения. Ускорения могут возникать при прямолинейном, криволинейном и вращательном движениях. Воспроизведение ускорений в процессе испытаний достигается, в основном, с помощью вращательного движения, создаваемого центрифугами. Криволинейное и вращательное движения могут быть равномерными и с ускорением. При равномерном криволинейном движении точки по окружности она проходит путь по дуге равный ΔS, или поворачивается на угол Δφ = ΔS/R, где R радиус окружности, по которой движется точка

Можно показать, что возникающее при указанном перемещении точки приращение вектора скорости приводит к возникновению нормального (центростремительного) ускорения, вектор которого направлен к центру окружности, а модуль определяется формулой

                                          (2.3.1.)

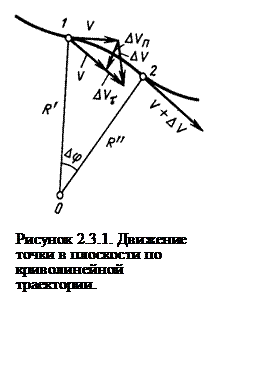
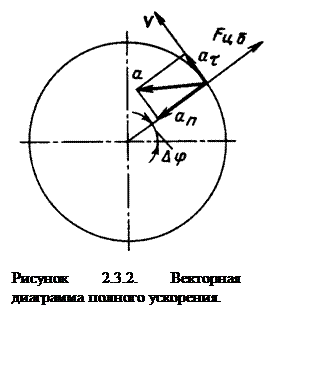
Очевидно, что чем больше искривлена траектория движения, т. е. чем меньше R, тем больше a_n при неизменной скорости. При криволинейном движении точки с ускорением (рисунок 2.3.1.), за время Δt вектор скорости  получает приращение . Для наглядности перенесем вектор в точку 1, чтобы его начало совпадало с началом вектора  Разложим вектор приращения скорости  на две составляющие.  и  для чего отложим от точки 1 на векторе  вектор , равный его модулю в начальный момент. В результате ряда преобразований получим вектор полного ускорения

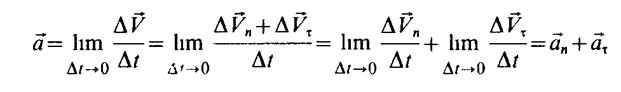       (2.3.2.)

Таким образом, вектор полного ускорения определяется суммой двух векторов , (рисунок 2.3.2.).

При равномерно ускоренном движении вектор  называемый тангенциальным (касательным) ускорением, направлен в сторону движения (совпадает с направлением скорости). При равномерно замедленном движении, направлен в сторону, противоположную направлению движения (скорости). Вектор , характеризует изменение скорости по величине. При неизменной скорости тангенциальное ускорение равно нулю и а=а_n, т. е. имеет место равномерное вращательное движение. Вектор  характеризует изменение скорости по направлению. При неизменном направлении скорости движение происходит по прямолинейной траектории = 0, и а =. Следовательно, чем больше радиус кривизны R, тем меньше . В общем случае модуль полного ускорения равен

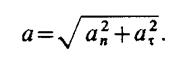                                        (2.3.3.)

Произвольное вращательное движение характеризуется угловой скоростью тела, векторная величина которой определяется выражением

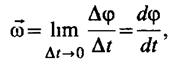                                       (2.3.4.)

где Δt-время, за которое совершается поворот на Δφ.

При постоянной угловой скорости имеет место равномерное вращение, при котором ω = φt. Учитывая, что угловая скорость одного оборота ω = 2π/n, и выражая его числом оборотов n в одну минуту, получим ω = πn/30 Гц.

При неравномерном вращении изменение вектора угловой скорости со временем характеризуется величиной

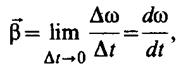                            (2.3.5.)

которая называется угловым ускорением. Модуль углового ускорения β=ω/T. При вращении отдельные точки вращающегося тела имеют различную касательную скорость V_τ, которая зависит от угловой скорости ω и от расстояния R данной точки от оси вращения. Полагая, что точка находится на расстоянии R от оси и проходит при вращении путь ΔS = RΔφ, получим линейную скорость

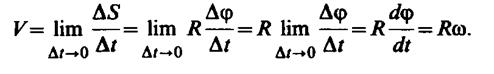                  (2.3.6.)

Таим образом, чем дальше отстоит точка от оси вращения, тем с большей линейной скоростью она вращается. Как уже было показано, a_n = V²/Rи, следовательно, a_n = ω²/R.

Аналогично модуль тангенциального (касательного