Задачи возникающие при проведении испытаний

Материалы практического занятия № 5.

Задачи возникающие при проведении испытаний.

*****

Применение графиков для анализа результатов испытаний. Исключение "анормальных" результатов измерений. Использование принципа накопления информации о надежности. Выводы об испытаниях на надежность. Особенности проектирования испытаний сложных технических систем на надежность.

*****

ПЗ.5.1. Применение графиков для анализа результатов испытаний

Процесс хода испытаний целесообразно каким-нибудь образом контролировать для выявления его основных тенденций. Один из методов такого контроля это нанесение полученных результатов на специальный график, в определенном масштабе. Масштаб подбирается так, чтобы функция распределения получалась на этом графике в виде прямой линии. Понятно, что это возможно, если определенным образом выбрать масштабы по осям графика. Поскольку вид функциональной зависимости исследуемого при проведении испытаний параметра может быть неизвестен, то масштаб выбирают для функциональной теоретической зависимости, которой по исходным предположениям должна следовать экспериментальная зависимость.

Для пояснения рассмотрим пример построения графика для случая, когда имеет место исследование времени до отказа для какой-то продукции и распределение этого времени описывается экспоненциальным законом.

                                        (ПЗ.5.1.)

Пусть предполагаемая функция распределения отказов будет иметь вид

.                                             (ПЗ.5.2.)

Функция, которая получается в результате испытаний, может быть записана в виде

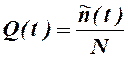,                                               (ПЗ.5.3.)

где n(t) – число отказов изделий из их общего числа Nк моменту времени t.

Введем некоторые обозначения. По оси абсцисс будем откладывать некоторую функцию времени S(t) связанную с истинным временем через некоторый коэффициент масштаба k_t, т.е.

.                                                            (ПЗ.5.4.)

Пусть максимальный размер оси абсцисс нашего графика равен , тогда значение коэффициента масштаба k_tможет быть получено из соотношения , откуда

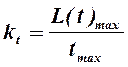,                                               (ПЗ.5.5.)

где t_max– предполагаемое максимальное время испытаний.

По оси ординат будем откладывать некоторую функцию  в масштабе , причем максимальное значение на оси ординат предположим равным . Для линеаризации предполагаемой функции распределения (ПЗ.5.1.) выберем функцию  в виде

                                                   (ПЗ.5.6.)

подставив λ из (ПЗ.5.2.) получим

,                                                (ПЗ.5.7.)

т.е. – значение , откладываемое по оси ординат в масштабе , который можно определить из выражения , откуда

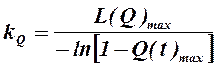.                                          (ПЗ.5.8.)

Пример. Построение графика для анализа испытаний по плану NUr

Как известно, план NUr отличается тем, что на испытания ставится N изделий, ремонт отказавших изделий в ходе испытаний не производится, испытания продолжаются до достижения количеством отказавших изделий величины r.

Построим график результатов испытаний и определим справедливость предположения об экспоненциальном характере распределения времени до отказа.

Для построения графика, примем такие исходные данные:

140 мм; 100 мм, предельное значение вероятности отказа . Предельное время проведения испытаний 700 час. На испытаниях по плану NUr поставлено 18 изделий. За время 400 час отказало 15 изделий. Распределение отказов по интервалам времени представлено статистическим рядом (см. таблицу ПЗ.5.1.).

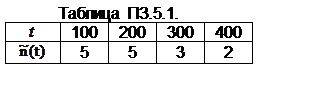Решение.

1.  Определим значение коэффициента масштаба по оси абсцисс

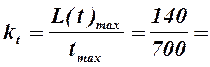0,2 мм/час.

2.  Определим значение коэффициента масштаба по оси ординат предполагая экспоненциальное распределение вероятности отказа F(t). Тогда

.

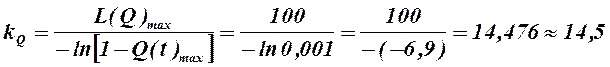3.  Зависимость функции вероятности отказов для различных моментов времени будем определять из экспериментальных данных используя выражение

.

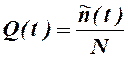4.  Значение функции выберем используя выражение (ПЗ.5.7.), т.е. . Поскольку аналитическое выражение функции Q(t) нам неизвестно, то используем значения функции Q(t) – полученные в эксперименте. Т.о.

.

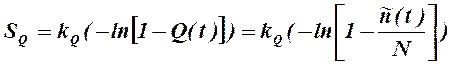На основании всего вышесказанного заполним таблицу (ПЗ.5.2.), а на ее основании построим график (см рисунок ПЗ.5.1.).

Прогнозируемые значения и  получаем в следующей последовательности:

1.  Значения , полученные на основании экспериментальных данных, наносим на график и соединяем линией. Убеждаемся что линия близка к прямой (т.е. наши исходные предпосылки о виде функции  верны и имеет место экспоненциальное распределение).

2.   Продолжаем прямую до пределов графика и из графика находим прогнозируемые значения . По значениям определяем .

Анализ данных таблицы и графика позволяет сделать выводы: