Теплові режими катоду – мішені МРС, страница 4

При решении задач теплопроводности широко используется метод тепловых потенциалов. Разработка метода тепловых потенциалов [13, 15] позволила в наиболее общей постановке свести обобщенную краевую задачу теплопроводности к системе уравнений Вольтера второго рода, разрешать которую в общем виде из – за сложности аналитического выражения не удается. Однако метод оказался особенно эффективным для равномерного движения границ. Были опубликованы решения для двухслойных задач теплопроводности с подвижной границей для областей. Однако все эти области имеют одинаковые теплофизические параметры и не отвечают реальным условиям напыления.

2.Математическоеописание тепловой задачи при наращивании покрытия на основу

Математическое описание тепловой задач при наращивании покрытия на основу должна содержать два уравнения теплопроводности (для покрытия и основы) и граничные условия четвертого рода на их общей границе. Кроме того, необходимо из конкретных тепловых режимов сформулировать граничные условия на внешних поверхностях. Полученная система должна быть дополнена уравнением движения границы кристаллизации для конденсации, найденным из анализа физических явлений на формирующейся поверхности, либо из экспериментальных данных.

Таким образом, математическое описание тепловой задачи, возникающей при наращивании покрытия на основу в форме пластины, можно записать следующим образом:

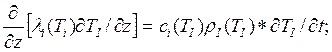
                                           (1.1)

;             при   z= 0              (1.2)

;                                            при   z= - h           (1.3)

;                                          при   z=           (1.4)

;                                                                                                                     (1.5)

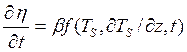,                                                                                                                     (1.6)

Для нахождения распределения температур необходимо проанализировать тепловые условия на границах системы покрытие – основа и получить в явном виде функции, входящие в уравнения (1.3) – (1.6).

3.Тепловые режимы при плазменном напылении в атмосфере

При плазменном напылении в результате взаимодействия нагретых частиц напыляемого материала и воздействия плазменной струи на поверхность происходит нагрев системы. Известно, [3, 16] что в этом случае частицы соударяются с поверхностью основы и затвердевают за время порядка с, а затем за время порядка с остывают до температуры основы. Причем затвердевания частиц происходит индивидуально. Заменяя процесс дискретного нанесения отдельных частиц моделью с непрерывным наращиванием покрытия, получаем, выделение теплоты при остывании частицы от конечной температуры нагрева  до температуры плавления ,выделения энергии кристаллизации и остывания частицы от  до температуры поверхности напыления , а также перехода кинетической энергии частицы в тепловую. Причем часть энергии частицы уходит в окружающее пространство в результате конвекции и теплоизлучения. Рассматривая физически малый объем на поверхности покрытия (рис.1) и составляя для него уравнения теплового баланса, получим при

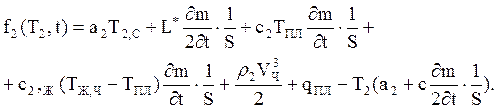               (1.7)

Внешняя сторона основы может охлаждаться в результате конвекции либо специальными охлаждающими приспособлениями, поддерживающими температуру этой поверхности постоянной. При плазменном напылении граница покрытия может двигаться с постоянной скоростью ,            либо скорость движения этой границы может быть периодической функцией времени

4.Тепловые режимы при плазменном напылении в вакууме

Для получения функций в явном виде, входящих в (1.3) – (1.6),при плазменном напылении в вакууме необходимо проанализировать тепловые явления на поверхности конденсации. В этом случае тепловые режимы системы покрытие – основа будут определятся тепловым потоком, падающем на поверхность конденсации, и условиями охлаждения основы.