































диэлектриком с относительной диэлектрической проницаемостью e = 4. Жила и оболочка выполнены из алюминия с удельной проводимостью g = 32·10 4 Cм/см. По кабелю протекает посто-янный ток I = 100 А при напряжении в рас-сматриваемом сечении U = 6 кВ.
Пренебрегая током утечки (проводи-мость изоляции принять равной нулю), определить закон изменения осевой составляющей вектора Пойнтинга через поперечное сечение изоляции. Найти поток вектора Пойнтинга через поперечное сечение изоляции. Найти потоки вектора Пойнтинга внутрь жилы и оболочки на единицу длины кабеля, с их помощью рассчитать сопротивления жилы и оболочки.
Решение
Вектор Пойнтинга рассчитывается через напряжённости
электрическо-го и магнитного полей ![]() =[
=[![]() ´
´![]() ]. Радиальная составляющая вектора напряжённости
электрического поля (см. раздел 12)
]. Радиальная составляющая вектора напряжённости
электрического поля (см. раздел 12)
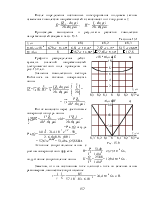
Er =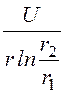 =
=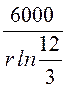 = 4330
= 4330![]() B/см при r[см].
B/см при r[см].
На поверхности жилы получаем Erж =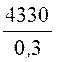 = 14400 B/см, на
внутренней поверхности оболочки Erоб =
= 14400 B/см, на
внутренней поверхности оболочки Erоб =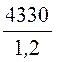 = 3610 B/см.
= 3610 B/см.
Напряжённость магнитного поля рассчитывается по закону полного тока и имеет только составляющую Ha. Для области диэлектрика
H = Ha =![]() =
=![]() ·
·![]() =
15,92·
=
15,92·![]() A/см при
r[см].
A/см при
r[см].
На поверхности жилы получаем Hж = 53,1 A/см, на внутренней стороне оболочки Hоб = 13,3 A/см.
Тангенциальная составляющая напряжённости электрического поля на поверхности жилы направлена вдоль положительного направления оси z (от генератора к нагрузке)
Etж =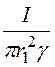 =
=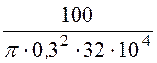 = 11,06·10 -4
B/см и
= 11,06·10 -4
B/см и ![]() =
=![]() Etж, на
поверхности оболочки тангенциальная составляющая направлена противоположно:
Etж, на
поверхности оболочки тангенциальная составляющая направлена противоположно:
Etоб =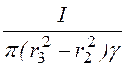 =
=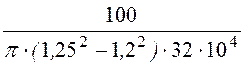 = 8,12·10-4
B/см и
= 8,12·10-4
B/см и ![]() =
-
=
-![]() Etоб.
Etоб.
Заметим, что тангенциальная составляющая напряжённости электриче-ского поля меньше радиальной на 7 порядков (отличается » в 107 раз).
Осевая составляющая вектора Пойнтинга, направленная от генератора к нагрузке,
Пz = Er·Ha =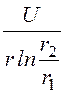 ·
·![]() = 68,92·103·
= 68,92·103·![]() Bт/см2 при r[см].
Bт/см2 при r[см].
Поток мощности через изоляцию кабеля
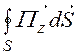 =
=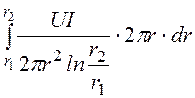 =
UI = 6000·100 = 6·105 Bт = Pн, то
есть энергия к приёмнику передаётся по изоляции кабеля и определяется
потребляемой мощностью нагрузки.
=
UI = 6000·100 = 6·105 Bт = Pн, то
есть энергия к приёмнику передаётся по изоляции кабеля и определяется
потребляемой мощностью нагрузки.
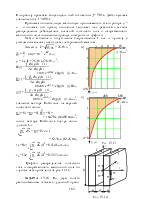
Поток энергии внутрь жилы на единицу длины l (рис. 15.5)
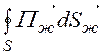 = Etж·Hж·2pr1l
=
= Etж·Hж·2pr1l
=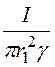 ·
·![]() ·2pr1l = I2
·2pr1l = I2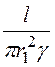 = I2
= I2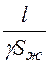 = DPж, где
DPж – мощность потерь в
жиле длиной l.
= DPж, где
DPж – мощность потерь в
жиле длиной l.
Формула 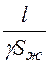 = Rж представляет собой
омическое (полученное на постоянном токе) сопротивление проводника. Таким
образом, на единицу длины l = 1 м = 100 cм получаем
= Rж представляет собой
омическое (полученное на постоянном токе) сопротивление проводника. Таким
образом, на единицу длины l = 1 м = 100 cм получаем
Rж =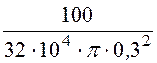 = 11,06·10 -4 ом, DPж =
11,06 Bт.
= 11,06·10 -4 ом, DPж =
11,06 Bт.
Тепловые потери в оболочке определяются потоком вектора Пойнтинга внутрь оболочки:
DPоб = Поб·Sоб = Etoб·Hoб·2pr2l =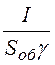 ·
·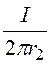 ·2pr2l = I2
·2pr2l = I2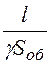 .
.
Сопротивление оболочки на единицу длины l = 1 м
Rоб =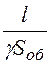 =
=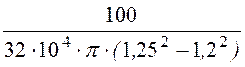 =
8,12·10 -4 ом,
=
8,12·10 -4 ом,
DPоб = I2Rоб = 1002·8,12·10 -4 = 8,12 Bт при длине кабеля l = 1 м.
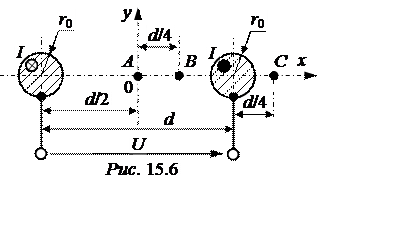 ЗАДАЧА 15.8.
По двухпровод-ной шине, расположенной в воздухе, с проводами одинакового
радиуса r0= 2 см, обладающими очень боль-шой удельной
проводимостью (g = ¥), замыкается ток I = 1 кА, как показано на рис. 15.6. Напряжение
между проводами U = 1 кВ.
ЗАДАЧА 15.8.
По двухпровод-ной шине, расположенной в воздухе, с проводами одинакового
радиуса r0= 2 см, обладающими очень боль-шой удельной
проводимостью (g = ¥), замыкается ток I = 1 кА, как показано на рис. 15.6. Напряжение
между проводами U = 1 кВ.
Рассчитать вектор Пойнтинга для точек А, В, С, лежащих на оси х, если расстояние между проводами d = 0,5 м.
Примечание. Так как d >> r0, смещением электрических осей от геометрических осей проводов пренебречь.
Ответ: ПA = 15,84·105 Bт/м2, ПB = 28,2·105 Bт/м2, ПC = 10,13·105 Bт/м2.
15.2. УРАВНЕНИЯ ПЕРЕМЕННОГО ЭЛЕКТРОМАГНИТНОГО ПОЛЯ В КОМПЛЕКСНОЙ ФОРМЕ. ВОЛНОВЫЕ УРАВНЕНИЯ.
При синусоидальном установившемся режиме переменного электромагнитного поля его характеристики выражаются с помощью комплексных амплитуд или комплексов действующих значений, когда мгновенные значения определяются соотношениями
![]() (wt) =
(wt) =![]() sin(wt +yE) = Im(
sin(wt +yE) = Im(![]()
![]() e jwt), где
верхняя стрелка обозначает, что рассматривается векторная величина, а нижняя
риска указывает на комплексную форму величины E = E
e jwt), где
верхняя стрелка обозначает, что рассматривается векторная величина, а нижняя
риска указывает на комплексную форму величины E = E![]() .
.
Выполнив операции
дифференцирования по времени, предусмотрен-ные уравнениями Максвелла для
мгновенных значений, опустив операцию «мнимая часть» и сократив на ![]() e jwt,
получают уравнения Максвелла в комплексной форме.
e jwt,
получают уравнения Максвелла в комплексной форме.
Запишем их в соответствии с подразд. 15.1:
1) 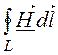 = I;
rot
= I;
rot![]() =
=![]() = g
= g ![]() + jw
+ jw
![]() = g
= g ![]() + jwee0
+ jwee0![]() при отсутствии тока
переноса;
при отсутствии тока
переноса;
2) 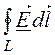 = -jwФ; rot
= -jwФ; rot
![]() = -jw
= -jw ![]() = -jwmm0
= -jwmm0![]() ;
;
3) 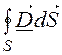 = q;
div
= q;
div ![]() = r;
= r;
4) 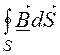 = 0; div
= 0; div ![]() = 0.
= 0.
Уравнения связи принимают вид
![]() = g
= g ![]() + jw
+ jw ![]() ,
, ![]() =
e0
=
e0![]() +
+
![]() =
ee0
=
ee0![]() ,
,
![]() = m0(
= m0(![]() +
+![]() ) = mm0
) = mm0![]() .
.
Граничные условия в комплексной форме определяются равенствами:
E1t = E2t, D1n = D2n – для диэлектриков;
E1t = E2t, d1n = d2n – для проводящих сред;
H1t = H2t, B1n = B2n – для магнитной составляющей поля.
Вводится комплексный вектор Пойнтинга ![]() =
=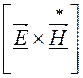 , где
, где ![]() – сопряжённый комплекс напряжённости
магнитного поля. Тогда
– сопряжённый комплекс напряжённости
магнитного поля. Тогда
-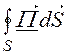 = P+ jQ
=
= P+ jQ
=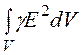 + 2jw
+ 2jw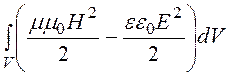 .
.
Для однородной изотропной среды при отсутствии
свободных зарядов q = 0, r = 0 в
соответствии с третьим уравнением Максвелла 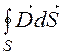 = 0, div
= 0, div ![]() = 0, div
= 0, div ![]() = 0, а 4 уравнения Максвелла сводятся к одному
уравнению:
= 0, а 4 уравнения Максвелла сводятся к одному
уравнению:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.