некоторому закону ![]() ставится в соответствие вполне
определённое действительное число
ставится в соответствие вполне
определённое действительное число ![]() , то говорят, что
, то говорят, что ![]() есть функция переменной величины
есть функция переменной величины ![]() и пишут
и пишут ![]() .
.
Множество ![]() называется областью
определения функции
называется областью
определения функции ![]() и обозначается
и обозначается ![]() . Множество всех значений
. Множество всех значений ![]() функции
функции ![]() , когда
, когда ![]() пробегает
всю область определения, называется областью изменения или областью
значений функции и обозначается
пробегает
всю область определения, называется областью изменения или областью
значений функции и обозначается ![]() .
.
Например, для функции ![]() область определения
область определения ![]() , область значений
, область значений ![]() .
.
Различают следующие способы задания функции: табличный, графический, аналитический (с помощью формул).
Под графиком
функции понимают множество точек плоскости, абсциссы которых есть
значения независимой переменной, а ординаты равны соответствующим значениям функции. График фукции есть некоторая
линия на плоскости. Например, уравнение ![]() задает функцию, графиком
которой является парабола.
задает функцию, графиком
которой является парабола.
К основным элементарным функциям относятся:
1.
![]() (при постоянном
(при постоянном ![]() ) — степенная функция;
) — степенная функция;
2. ![]() (при постоянном
(при постоянном ![]() ,
, ![]() ,
, ![]() ) — показательная функция;
) — показательная функция;
3. ![]() (при постоянном
(при постоянном ![]() ,
, ![]() ,
, ![]() ) — логарифмическая функция;
) — логарифмическая функция;
4. ![]() —
тригонометрические функции;
—
тригонометрические функции;
5. ![]() — обратные тригонометрические функции.
— обратные тригонометрические функции.
Функция, заданная
последовательной цепью нескольких функций (![]() , где
, где ![]() ), называется сложной функцией.
Например, функция
), называется сложной функцией.
Например, функция ![]() сложная, и она может быть представлена следующей цепью
основных элементарных функций:
сложная, и она может быть представлена следующей цепью
основных элементарных функций: ![]() .
.
Функции,
образованные из основных элементарных функций посредством конечного числа
алгебраических операций и взятия функции от функции, называются элементарными.Все остальные функции называются неэлементарными.
Примером неэлементарной функции может служить функция вида ![]()
Функция, определяемая уравнениями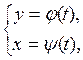 в которых зави-симость между
в которых зави-симость между![]() и
и![]() устанавливается
посредством третьей
перемен-ной
устанавливается
посредством третьей
перемен-ной ![]() ,называется заданной параметрически,
при этом
,называется заданной параметрически,
при этом ![]() —параметр.
—параметр.
Например, уравнения ![]() определяют ли-нейную функцию
определяют ли-нейную функцию![]() .
.
§2. Предел числовой последовательности. Предел функции
Определение. Число ![]() называется пределом
последователь-ности
называется пределом
последователь-ности ![]() если для любого положительного числа
если для любого положительного числа ![]() существует такой номер
существует такой номер ![]() , что при всех
, что при всех ![]() выполняется неравенство
выполняется неравенство ![]() .
.
Если последовательность ![]() имеет своим
пределом число
имеет своим
пределом число ![]() , то это записывается следующим
образом
, то это записывается следующим
образом ![]() .
.
Определение. Число А называется пределом
функции![]() в точке
в точке ![]() ,
если для каждого числа
,
если для каждого числа ![]() найдется такое число
найдется такое число ![]() , что при
, что при ![]() выполняется неравенство
выполняется неравенство ![]() .
.
Обозначают
этот факт так: ![]() .
.
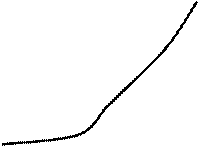
Если число ![]() является пределом функции
является пределом функции ![]() в точке
в точке ![]() , то на графике это иллюстрируется следующим образом. Так как из неравенства
, то на графике это иллюстрируется следующим образом. Так как из неравенства ![]() следует
неравенство
следует
неравенство ![]() , то это значит, что для всех
, то это значит, что для всех ![]() ,
отстоящих от
,
отстоящих от ![]() не далее чем на
не далее чем на ![]() ,
точка
,
точка ![]() графика функции
графика функции ![]() лежит внутри полосы шириной
лежит внутри полосы шириной ![]() ,
ограниченной прямыми
,
ограниченной прямыми ![]() и
и ![]() . Очевидно, что с уменьшением
. Очевидно, что с уменьшением ![]() величина
величина
![]() также уменьшается (см. рис.3.1).
также уменьшается (см. рис.3.1).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() M
M
![]()
![]()
![]()
![]()
0 ![]()
![]()
![]()
![]()
Рис.3.1
Число ![]() называется пределом
функции
называется пределом
функции ![]() в
точке
в
точке![]() , если для любого
, если для любого ![]() существует число
существует число ![]() , что при всех
, что при всех ![]() выполняется неравенство
выполняется неравенство ![]() .
.
Функция ![]() называется
ограниченной в области D, если
существует постоянное число
называется
ограниченной в области D, если
существует постоянное число ![]() , что для всех
, что для всех ![]() выполняется неравенство
выполняется неравенство ![]() .
.
Например,
функция ![]() ограничена для всех
ограничена для всех![]() , так
как в этой области
, так
как в этой области ![]() .
.
§3. Бесконечно малые и бесконечно большие величины
Определение. Величина ![]() называется
бесконечно малойвеличиной в точке
называется
бесконечно малойвеличиной в точке![]() , если
, если ![]() .
.
Величина ![]() называется
бесконечно большой величиной в
точке
называется
бесконечно большой величиной в
точке ![]() ,если
,если
![]() .
.
Например, функция ![]() является бесконечно малой в точке
является бесконечно малой в точке ![]() , а функция
, а функция ![]() есть бесконечно малая в точках
есть бесконечно малая в точках ![]() ,
так как их пределы в соответствующих точках равны нулю. Функция
,
так как их пределы в соответствующих точках равны нулю. Функция ![]() является бесконечно малой в точке
является бесконечно малой в точке ![]() и бесконечно большой в точке
и бесконечно большой в точке ![]() .
.
Теорема. Если ![]() — бесконечно малая величина в точке
— бесконечно малая величина в точке ![]() , то
, то ![]() —бесконечно большая величина в этой же точке
—бесконечно большая величина в этой же точке ![]() .
.
Если ![]() —
бесконечно большая величина в точке
—
бесконечно большая величина в точке ![]() , то
, то ![]() -
бесконечно малая величина
в этой же точке (
-
бесконечно малая величина
в этой же точке (![]() ).
).
(Доказательство см. [1], гл. II, §4.)
Справедливы следующие утверждения:
1. Сумма конечного числа бесконечно малых величин есть бесконечно малая величина.
2. Произведение ограниченной величины на бесконечно малую величину есть бесконечно малая величина.
3. Произведение конечного числа бесконечно малых величин есть бесконечно малая величина.
§4. Теоремы о пределах
Если пределы ![]() и
и ![]() существуют и
конечны, то
существуют и
конечны, то
1. ![]() , где с –
const;
, где с –
const;
2. ![]()
![]() +
+![]() ;
;
3. ![]()
![]()
![]() ;
;
4. 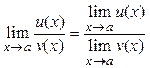 , где
, где ![]() .
.
Замечательные пределы.
Первый замечательный предел: ![]() .
.
Второй замечательный предел:
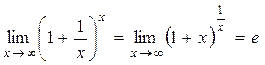 ,
где
,
где ![]() — иррациональное число,
— иррациональное число, ![]() — одна из фундаментальных величин в
математике. Оно определяет, например, функции:
— одна из фундаментальных величин в
математике. Оно определяет, например, функции: ![]() ,
которая называется экспонентой;
,
которая называется экспонентой;
![]() ,
которая называется натуральным логарифмом.
,
которая называется натуральным логарифмом.
Пример 3.1. Вычислить 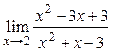 .
.
Так как ![]() , то применима теорема о пределе
частного. Значит,
, то применима теорема о пределе
частного. Значит, 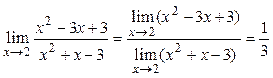 .
.
Пример 3.2. Вычислить 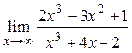 .
.
Так как при ![]() числитель и знаменатель дроби, стоящей под знаком предела,
стремятся к бесконечности, то имеем неопределенность вида
числитель и знаменатель дроби, стоящей под знаком предела,
стремятся к бесконечности, то имеем неопределенность вида ![]() . Для раскрытия таких неопределенностей делят числитель и
знаменатель дроби на старшую степень
. Для раскрытия таких неопределенностей делят числитель и
знаменатель дроби на старшую степень ![]() . После деления на
. После деления на ![]() получаем:
получаем:
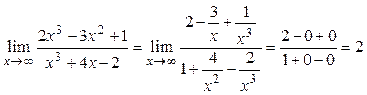 .
.
Пример
3.3. Вычислить 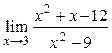 .
.
Так как ![]() , то имеем неопре-делённость вида
, то имеем неопре-делённость вида ![]() .
Разложим числитель и знаменатель дроби на линейные множители. Так как
.
Разложим числитель и знаменатель дроби на линейные множители. Так как ![]() при
при ![]() и
и ![]() , то
, то
![]() . Тогда
. Тогда 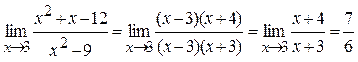 .
.
Пример
3.4. Вычислить  .
.
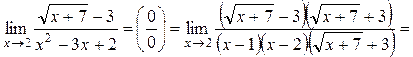

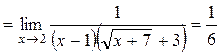 .
.
Пример
3.5. Вычислить 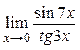 .
.
Для раскрытия неопределённости ![]() воспользуемся первым замечательным пределом. Считая,
что
воспользуемся первым замечательным пределом. Считая,
что ![]() , проведём очевидные преобразования:
, проведём очевидные преобразования: 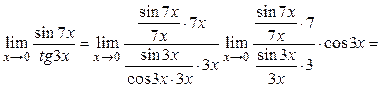
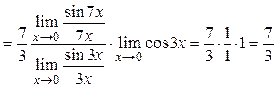 .
.
Пример
3.6. Вычислить 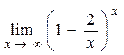 .
.
Для раскрытия неопределённости ![]() воспользуемся
вторым замечательным пределом:
воспользуемся
вторым замечательным пределом: 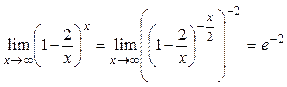 , поскольку
, поскольку 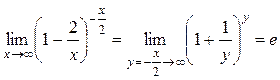 .
.
§5. Сравнение бесконечно малых величин
Для сравнения двух бесконечно
малых величин ![]() и
и ![]() в точке
в точке
![]() находят предел отношения
находят предел отношения 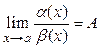 .
.
Если ![]() и
и ![]() товеличины
товеличины ![]() и
и ![]() называются бесконечно малыми одного порядка.
называются бесконечно малыми одного порядка.
Если ![]() , то
, то
![]() называется бесконечно малой высшего порядка по сравнению с
называется бесконечно малой высшего порядка по сравнению с![]() .
Записывается это так:
.
Записывается это так: ![]() .
.
Если ![]() , то
бесконечно малые величины
, то
бесконечно малые величины ![]() и
и
![]() называют эквивалентным и обозначают
называют эквивалентным и обозначают ![]() . Например,
. Например, ![]() в
точке
в
точке ![]() , так как
, так как ![]() .
.
Основные эквивалентности в точке ![]() :
:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
При вычислении пределов используют следующую теорему.
Теорема.Предел отношения двух бесконечно малых величин в некоторой точке равен пределу отношения эквивалентных им бесконечно малых величин в той же точке.
Доказательство см. [1], гл. II, §11.
Пример
3.7. Вычислить
![]() .
.
Воспользуемся эквивалентными бесконечно
малыми величинами. Так как при ![]()
![]() и
и ![]() , то
, то 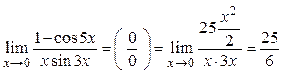 .
.
§6. Непрерывность функции
Определение. Функция ![]() называется непрерывной в точке
называется непрерывной в точке ![]() , если
предел функции в точке
, если
предел функции в точке ![]() существует и
существует и ![]() .
.
Односторонними называются пределы:
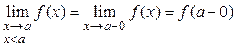 - левосторонний
предел в точке
- левосторонний
предел в точке ![]() ;
;
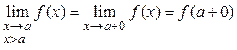 - правосторонний
предел в точке
- правосторонний
предел в точке ![]() .
.
Определение. Функция ![]() называется непрерывной в точке
называется непрерывной в точке ![]() , если
существуют односторонние пределы в точке
, если
существуют односторонние пределы в точке ![]() и
и ![]() . (*)
. (*)
Если односторонние пределы конечны, но
нарушается хотя бы одно из равенств (*), то ![]() называется точкой разрыва 1-го рода.
называется точкой разрыва 1-го рода.
Если хотя бы один из этих односторонних
пределов не существует или равен бесконечности, то ![]() называется точкой
разрыва второго рода.
называется точкой
разрыва второго рода.
![]() Например,
функция
Например,
функция 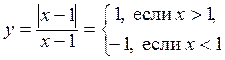 ,
имеет в точке
,
имеет в точке ![]() разрыв
1-го рода (рис. 3.2). y
разрыв
1-го рода (рис. 3.2). y
![]()
![]()
![]() 1
1
![]()
![]() 0 1 x
0 1 x
![]() -1
-1
Рис. 3.2
Функция ![]() имеет в точке
имеет в точке ![]() разрыв второго рода (рис.3.3).
разрыв второго рода (рис.3.3).
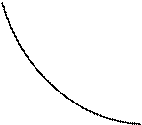
![]()
![]() y
y
![]()
 0 2 x
0 2 x
Рис.3.3
Если функция непрерывна во всех точках
отрезка ![]() ,
то она называется непрерывной на этом отрезке.
,
то она называется непрерывной на этом отрезке.
Из определения непрерывности функции и теорем о пределах следуют теоремы:
I. Если
функции ![]() и
и
![]() непрерывны
в точке
непрерывны
в точке ![]() ,
то в этой точке непрерывны функции
,
то в этой точке непрерывны функции ![]() ,
, ![]() ,
,  .
.
II. Сложная функция, составленная из непрерывных функций, непрерывна в соответствующей точке.
III. Всякая элементарная функция непрерывна в каждой точке своей области определения.
Доказательство приведено, например, в [1], гл. II, §9.
РАЗДЕЛ 4. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
§1. Производная функции,её геометрический и механический смысл
Пусть функция ![]() определена в некоторой окрестности точки х.
Если переменная х получит приращение
определена в некоторой окрестности точки х.
Если переменная х получит приращение ![]() , то функция у получит приращение
, то функция у получит приращение ![]() .
.
Определение. Производной функции ![]() в точке х
называется предел отношения приращения функции
в точке х
называется предел отношения приращения функции ![]() к приращению аргумента
к приращению аргумента ![]() , когда
, когда ![]() , т.е.
, т.е.
![]() .
.
Для
производной функции ![]() в точке х применяют также обозначения:
в точке х применяют также обозначения:
![]() .
.
Функция, имеющая в данной точке конечную производную, называется дифференцируемой в этой точке.
Геометрический смысл производной. Построим график функции ![]() и проведём к нему касательную через точку
и проведём к нему касательную через точку ![]() (рис.4.1).
Обозначим через
(рис.4.1).
Обозначим через ![]() угол,
образованный этой касательной c осью
угол,
образованный этой касательной c осью ![]() , тогда
, тогда
![]() , т.е.
производная
, т.е.
производная ![]() функции
функции ![]() равна угловому коэффициенту касательной к графику
этой функции в точке с абсциссой
равна угловому коэффициенту касательной к графику
этой функции в точке с абсциссой ![]() .
.
![]()

 y
y
![]()
![]()
![]()
![]()
![]()
![]() α
α
0 x0 x
Рис.4.1
Уравнение касательной к
кривой ![]() в
точке
в
точке ![]() имеет
вид
имеет
вид
![]() , а уравнение
нормали к данной кривой в этой же точке записывается в виде
, а уравнение
нормали к данной кривой в этой же точке записывается в виде
![]() при
условии, что
при
условии, что ![]() .
.
Если
![]() , то
уравнение касательной:
, то
уравнение касательной: ![]() , а уравнение нормали:
, а уравнение нормали: ![]() .
.
Механический смысл производной. Пусть материальная точка движется прямолинейно по
закону ![]() .
Тогда
.
Тогда ![]() , т.е. производная
от пути по времени есть скорость движения точки.
, т.е. производная
от пути по времени есть скорость движения точки.
§2. Основные правила дифференцирования
Если функции ![]() и
и ![]() дифференцируемы, то
дифференцируемы, то
1.
![]() ,
, ![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
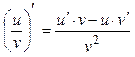 ,
, ![]() .
.
5.
Если ![]() и
и ![]() -
дифференцируемые функции своих аргументов, то сложная функция
-
дифференцируемые функции своих аргументов, то сложная функция ![]() тоже
дифференцируема и
тоже
дифференцируема и
![]() или
или ![]() .
.
Это правило легко распространить на цепочку из любого конечного числа дифференцируемых функций.
6.
Если для дифференцируемой функции ![]()
![]() существует обратная функция
существует обратная функция ![]() , то
, то
 или
или 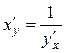 .
.
§3. Таблица производных основных элементарных функций
В
приводимой ниже таблице:![]() ;
;![]() ;
;![]() ,
,![]() ;
;![]() .
.
|
|
||
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство справедливости указанных формул смотрите в [1], гл.III, §5, 6, 8, 10, 12, 14.
Пример
4.1. Найти производную функции ![]() .
.
Данную функцию представляем в виде![]() . Тогда
. Тогда 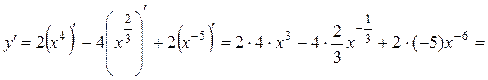
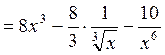 .
.
Пример
4.2. Найти производную функции ![]() .
.
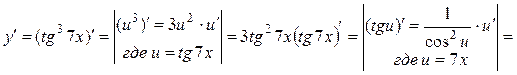
 .
.
Здесь при решении указывались формулы, которые применялись при вычислении производных.
Пример
4.3. Найти производную функции ![]() .
.
Последовательно используем формулы для производных сложных функций
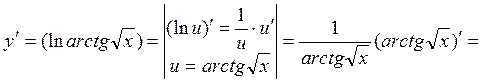
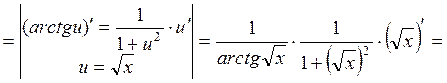
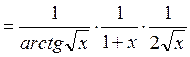 .
.
Пример
4.4. Найти производную функции ![]() .
.
Применим формулу производной произведения
![]()
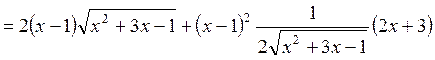 .
.
Пример
4.5. Найти производную функции 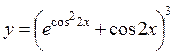 .
.
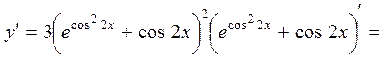
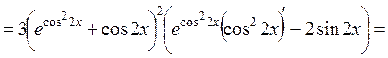
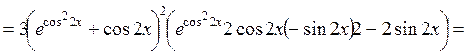
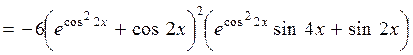 .
.
§4. Дифференциал функции, его геометрический смысл.
Правила дифференцирования
Если функция ![]() дифференцируема в точке
дифференцируема в точке ![]() , то существует
конечный предел
, то существует
конечный предел
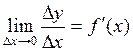 .
.
Отсюда следует, что 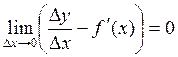 , т.е.
, т.е. 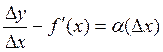 , где
, где ![]() - бесконечно малая величина
- бесконечно малая величина 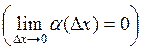 . Это
значит, что приращение функции
. Это
значит, что приращение функции ![]() , соответствующее приращению аргумента
, соответствующее приращению аргумента ![]() , может быть
представлено в виде
, может быть
представлено в виде ![]() .
.
Определение.
Дифференциалом ![]() функции
функции ![]() в точке
в точке ![]() называется главная линейная часть приращения функции
в этой точке, т.е.
называется главная линейная часть приращения функции
в этой точке, т.е.
![]() .
.
Обозначая ![]() , получим формулу
, получим формулу
![]() или
или ![]() , т.е.
дифференциал функции равен произведению производной этой функции на
дифференциал аргумента.
, т.е.
дифференциал функции равен произведению производной этой функции на
дифференциал аргумента.
Геометрический смысл дифференциала функции. Дифференциал функции ![]() равен приращению ординаты касательной, проведённой к
графику этой функции в точке
равен приращению ординаты касательной, проведённой к
графику этой функции в точке ![]() , когда аргумент получает приращение
, когда аргумент получает приращение ![]() (рис.4.2).
(рис.4.2).
 |
|||
![]()
![]()
 |

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
0 ![]()
![]()
![]()
Рис.4.2
Пример
4.6. Найти дифференциал функции ![]() .
.
Находим производную ![]() . Тогда
. Тогда ![]() .
.
Если ![]() - постоянная,
- постоянная, ![]() - дифференцируемые функции, то справедливы следующие правила
нахождения дифференциалов:
- дифференцируемые функции, то справедливы следующие правила
нахождения дифференциалов:
1.
![]() ,
,
2.
![]() ,
,
3.
![]() ,
,
4.
![]() ,
,
5.
![]() ,
,
6.
![]() .
.
§5. Производные и дифференциалы высших порядков
I.
Производной ![]() -ого
порядка называют производную, взятую
от производной
-ого
порядка называют производную, взятую
от производной ![]() -го порядка,
т.е.
-го порядка,
т.е.
![]() .
.
Согласно
этому определению производная порядка ![]() любой функции находится последовательным её
дифференцированием
любой функции находится последовательным её
дифференцированием ![]() раз, т.е. для функции
раз, т.е. для функции ![]() имеем
имеем
![]()
Для обозначения производной ![]() -го порядка
применяются символы
-го порядка
применяются символы
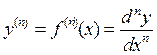 .
.
Физический смысл второй производной. Так как производная любой функции равна скорости её
изменения в данной точке, то вторая производная от пути по времени равна
ускорению движения точки в данный момент времени, т.е. ![]() .
.
II.
Дифференциалом ![]() -ого
порядка функции
-ого
порядка функции ![]() называется
дифференциал, взятый от дифференциала
называется
дифференциал, взятый от дифференциала ![]() -го порядка, т.е.
-го порядка, т.е.
![]() .
.
Откуда
следует, что ![]() ,
т.к.
,
т.к. ![]() не зависит
от
не зависит
от ![]() . Аналогично
получаем
. Аналогично
получаем
![]() .
.
Пример
4.7. Найти производную и дифференциал
второго порядка функции ![]() .
.
Находим первую производную
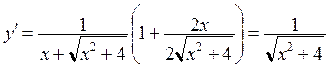 .
.
Следовательно,
![]() .
.
Дифференцируя первую производную, получаем
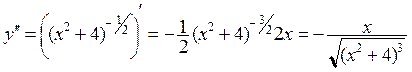 , значит
, значит ![]() .
.
§6. Правило Лопиталя и его применение к
раскрытию неопределённостей
Теорема. Пусть
функции ![]() и
и
![]() непрерывны
на отрезке
непрерывны
на отрезке ![]() , дифференцируемы на интервале
, дифференцируемы на интервале ![]() и в
точке
и в
точке ![]() одновременно обращаются в нуль или равны бесконечности. Тогда, если
существует предел
одновременно обращаются в нуль или равны бесконечности. Тогда, если
существует предел 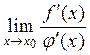 , то справедливо равенство
, то справедливо равенство 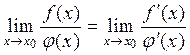 .
.
Правило применимо и в случае, когда ![]() .
.
Пример
4.8. Найти 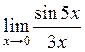 .
.
Так
как функции ![]() и
и
![]() непрерывны
и дифференцируемы в точке
непрерывны
и дифференцируемы в точке ![]() и
и ![]() ,
то применяя правило Лопиталя, получим
,
то применяя правило Лопиталя, получим 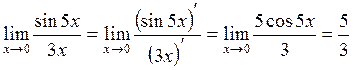 .
.
Пример
4.9. Найти 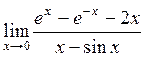 .
.
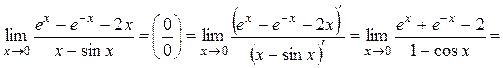
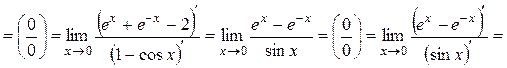
 .
.
РАЗДЕЛ 5. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ПОСТРОЕНИЮ ИХ ГРАФИКОВ
§1. Возрастание и убывание функции. Экстремум функции
Определение.
Если для всех точек интервала ![]() при
при ![]() выполняется
неравенство
выполняется
неравенство ![]() ,
то функция называется возрастающей (убывающей) на
,
то функция называется возрастающей (убывающей) на ![]() .
.
Признаки возрастания (убывания) функции.
1.
Если функция ![]() дифференцируема
на интервале
дифференцируема
на интервале ![]() и возрастает (убывает), то
и возрастает (убывает), то ![]() для
любых
для
любых ![]() .
.
2.
Если функция ![]() дифференцируема
на интервале
дифференцируема
на интервале ![]() и
и ![]() , то она возрастает (убывает) на
, то она возрастает (убывает) на ![]() .
.
Определение.
Точка ![]() называется точкой
максимума (минимума) функции
называется точкой
максимума (минимума) функции ![]() , если
существует такая окрестность точки
, если
существует такая окрестность точки ![]() , что для любых
, что для любых ![]() из этой окрестности
из этой окрестности ![]() .
.
![]() Точки, в
которых функция достигает максимума или минимума, называются точками
экстремума функции, а значения функции в этих точках называют экстремальными.
Точки, в
которых функция достигает максимума или минимума, называются точками
экстремума функции, а значения функции в этих точках называют экстремальными.
 |
![]()
![]()
![]() 0
0 ![]()
![]()
![]()
![]() Рис.5.1
Рис.5.1
Функция, заданная кривой на рис.5.1, в точках ![]() и
и ![]() достигает
максимума, а в точке
достигает
максимума, а в точке ![]() - минимума.
- минимума.
Необходимый признак экстремума. В точке экстремума производная функции равна нулю или не существует.
Функция ![]() (рис.5.1) в точках
(рис.5.1) в точках ![]() и
и ![]() имеет производную равную нулю. Касательные к кривой в этих точках
параллельны оси
имеет производную равную нулю. Касательные к кривой в этих точках
параллельны оси ![]() .
Но функция может достигать экстремума и в точках, в которых производная не
существует (точка
.
Но функция может достигать экстремума и в точках, в которых производная не
существует (точка ![]() ).
).
Достаточный признак экстремума. Пусть функция ![]() дифференцируема в некотором интервале, содержащем
критическую точку
дифференцируема в некотором интервале, содержащем
критическую точку ![]() , кроме, быть может, самой точки
, кроме, быть может, самой точки ![]() .
Тогда, если при переходе через критическую точку производная
.
Тогда, если при переходе через критическую точку производная ![]()
1)
меняет знак с + на – , то в
точке ![]() функция имеет максимум;
функция имеет максимум;
2)
меняет знак с – на +, то в
точке ![]() функция имеет минимум;
функция имеет минимум;
3)
не меняет знак, то в точке ![]() нет
экстремума.
нет
экстремума.
Схема исследования функции на экстремум с помощью первой производной:
![]()
![]()
![]()
![]()
![]()
![]() +
+ ![]() –
– ![]() +
+  +
+ ![]()
Пример 5.1.
Исследовать на экстремум функцию ![]() .
.
Находим критические точки данной функции
![]()
![]()
![]()
Исследуем знак производной при переходе через критические
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.