Задача линейного программирования. Три типа оборудования

ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

(Н. П. Чурляева учеб. пособие «Методы математического моделирования». – САА, Красноярск 2001)

Все задачи математического программирования сводятся к одной общей постановке: найти значения переменных х₁, х₂...... х_n, доставляющих max(min) заданной целевой функции F(х_1, х₂,..., х_n)и удовлетворяющих одновременно ряду условий – ограничениям:

g_i (x₁, x₂,...x_n) < > b_i;                  i = 1, 2,...., m;       x_j > 0.   (1)

Задача линейного программирования возникает, если целевая функция F и все ограничения g_i линейны относительно х₁,х₂,..., х_n , т.е.:

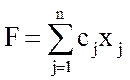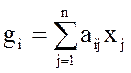;                  ;      i = 1,…, m.  (2)

Рассмотрим возникновение задачи линейного программирования и один из методов ее решения на примере одной технологической задачи. Допустим, для изготовления двух изделий А₁ и А₂ используется три типа оборудования: токарное, сварочное и шлифовальное. Для каждой операции известно время обработки одного изделия. Известны также общий фонд (лимит) рабочего времени оборудования каждого типа и прибыль от реализации одного изделия типа А₁ или А₂.

Таблица

Требуется определить, сколько изделий и какого типа необходимо изготовить для получения максимальной прибыли от реализации.

Предположим, изготовлено x₁ изделия типа А₁ и х₂ изделий типа А₂. Тогда на их изготовление пошло всего 12·х₁ + 4·x₂, станко-часов токарного оборудования. Поскольку общий фонд рабочего времени токарных станков не может превышать 300 станко-часов, то имеет место неравенство

12·x₁ + 4·x₂ < 300                                          (3)

Аналогично для сварочных и шлифовальных работ получаем еще два неравенства:

4·x₁ + 4·x₂ < 120,                                           (4)

3·x₁ + 12·x₂ < 250.

Кроме того, два неравенства возникает из факта неотрицательности числа изделия:

x₁ > 0,            x₂ > 0.                                                 (5)

Прибыль от реализации x₁ изделий типа A₁ и x₂ изделий типа A₂ составит F = 30x₁ + 40x₂, млн. р.

Геометрическая интерпретация поставленной задачи линейного программирования довольно проста в силу двумерности задачи и заключается в следующем. Ограничения (3), (4), (5) определяют выпуклую область допустимых решений задачи, называемую многоугольником решений. Стороны этого многоугольника задаются прямыми, уравнения которых получаем из ограничений (3), (4), (5) заменой знаков >, < на знак равенства.

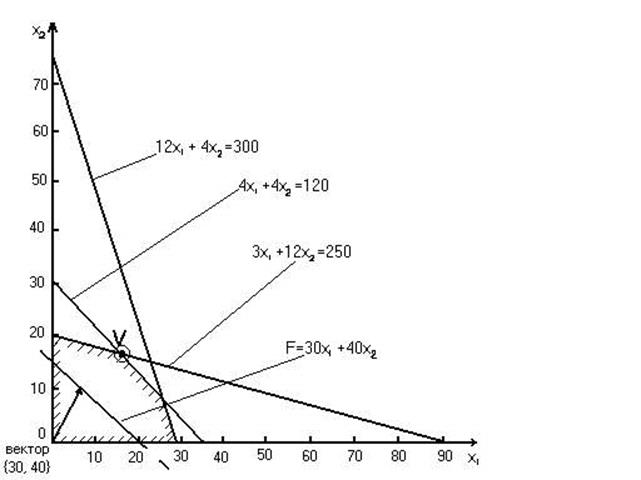
Рис. 1. Графическое решение задачи линейного программирования

Можно показать, что целевая функция F принимает максимальное значение в одной из вершин заштрихованного многоугольника, а именно в вершине V. Чтобы найти искомую вершину, строим прямую постоянного уровня 30·x₁ + 40·x₂ = F и перемещаем ее параллельно самой себе, т.е. вдоль вектора (30, 40) до тех пор, пока не  достигнем границы области допустимых решений. Вершина V является точкой пересечения двух прямых, поэтому ее координата определяются решением системы уравнений

4·x₁ + 4·x₂ = 120,

3·x₁ + 12·x₂ = 250.

Решив эту систему, получим , . Следовательно, изготовив 12 изделий типа А₁ и 18 изделий типа А₂, получим максимально возможную прибыль

F^max   30 × 12 + 40 × 18 = 1080 млн.р.

Если к изделиям А₁ и А₂ добавить изделие А₃, то геометрическая интерпретация поставленной задачи поиска максимума прибыли усложняется, поскольку от двумерного (плоского) случая переходим к трехмерному (пространственному). Тем не менее и в случае n = 3 возможно наглядное геометрическое решение задачи. Для этого производим следующие действия:

1.  Вместо прямых, задаваемых неравенствами типа (3), (4), (5), строим плоскости

g_i  = a_i1 · x₁ + a_i2 · x₂ + a_i3 · x₃ = b_i;        i = 1, 2,…, m.

2.         Находим области, определяемые каждым i–м ограничением задачи.

3.         Вместо многоугольника решений определяем многогранник решений.

4.         Вместо прямой постоянного уровня строим плоскость, задаваемую целевой функцией F = с₁ · x₁ + с₂ · x₂ + c₃ · x₃ и пересекающую многогранник решений.

5.         Строим вектор  нормальный плоскости постоянного уровня.

6.  Перемещаем плоскость постоянного уровня вдоль вектора С до тех пор, пока не достигнем вершины V многогранника решений, в которой