Пример выполнения контрольной работы «Реализация плана полного факторного эксперимента типа 22»

ПРИМЕР ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ

«РЕАЛИЗАЦИЯ ПЛАНА ПОЛНОГО ФАКТОРНОГО ЭКСПЕРИМЕНТА ТИПА 2²»

Пример приводится из методических указаний «Математическое моделирование технологических процессов в машиностроении» / П.А. Снетков. – СибГАУ, 2006. – 52 с.

ИСХОДНЫЕ ДАННЫЕ:

При зенкеровании  отверстий зенкером из быстрорежущей стали Р6М5, в детали из закаленной стали 12Х18Н9Т, измерялись осевые силы резания Р_о. Каждое измерение повторялось дважды n = 2. Данные занесены в табл. 1.

Таблица 1. Осевые силы резания Р_о, Н

Табличные значения критериев Фишера, Стьюдента и Кохрена, для заданных условий, соответственно: F_0.05 (1, 4) = 224,6;    t_0.05 (4) = 2.776;    G_0.05 (1, 4) = 0.996

Задание:

Получить уравнение регрессии Р_о = b₀ + b₁t + b₂S_o и построить графики функций:

для t = 0,5 мм Р_о = b₀ + 0,5 × b₁ + b₂S_o;

для t = 1,0 мм Р_о = b₀ +  b₁ + b₂S_o;

для  t = 1,5 мм Р_о = b₀ + 1,5 × b₁ + b₂S_o.

Провести дисперсионный анализ, проверить однородность дисперсий, определить значимость коэффициентов регрессии, проверить адекватность полученной модели реальной поверхности отклика.

РЕШЕНИЕ:

В качестве первого переменного фактора X₁ выбираем глубину резания t, в качестве второго фактора X₂ выбираем подачу S, в качестве отклика Y принимаем осевую силу резания Р_о. Определяем шаг и уровни варьирования факторов данные заносим в таблицу 2.

Таблица 2. Исходные данные для планирования эксперимента

Расчет шага варьирования:

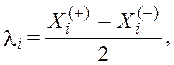                       (1)

Расчет основного уровня:

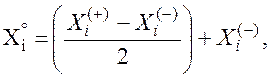        (2)

Производим кодирование факторов по формуле:

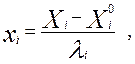                                            (3)

где x_j — кодированное значение фактора, X_i — натуральное значение фактора,

X^o_i  — натуральное значение основного уровня,

l_i — интервал варьирования,i — номер фактора.

1.  Заполняем таблицу 2.

Условия четырех измерений, кодированные в соответствии с формулой (3), приведены в графах 2 и 3 табл. 3. Результаты измерений помещены в графы 4 и 5 табл. 3.

Графы 6 и 7  заполняются результатами вычислений по формулам

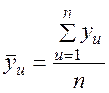              –   среднее арифметическое           (4)

и

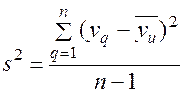 – дисперсия            (5)

причем в связи с тем, что çy_u1-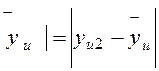 при n = 2, формула (5) упрощается:

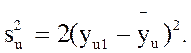
Таблица 2. Результаты реализации плана ПФЭ типа 2²

Выборочные оценки s²_u можно считать однородными, поскольку выполняется неравенство

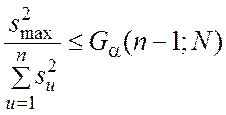              (6)

где  – наибольшая из дисперсий,

 – табличное значение критерия Кохрена.

Вычисляем дисперсию воспроизводимости среднего значения функции по формуле:

;

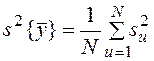Рассчитываем  коэффициенты регрессии:

;                         

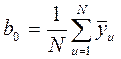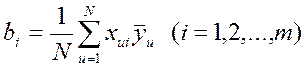, где m – количество факторов;

Определяем дисперсии коэффициентов регрессии

;                              

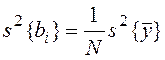Все коэффициенты b_i проверяем на значимость, так как выполняется условие:

 t_0,05  (4) то линейное уравнение регрессии имеет вид:

Далее заполняем графы 8 и 9 табл. 2 и проверяем гипотезу об адекватности полученной модели реальной поверхности отклика.

Остаточная дисперсия равна

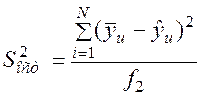
где f₂ – количество степеней свободы,

Гипотеза об адекватности полученной модели реальной поверхности отклика не отвергается, так как выполняется условие

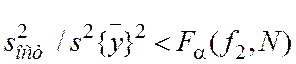
где – табличное значение критерия Фишера.

Раскодирование линейных уравнений регрессии производится по формуле:

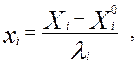
Подставляем значения x₁ и x₂ в уравнения регрессии и получаем линейное уравнение регрессии в раскодированном виде:

Получаем искомое уравнение регрессии:

Строим графики функции (рис. 1)