Санкт-Петербургский государственный морской технический университет
КАФЕДРА СТРОИТЕЛЬНОЙ МЕХАНИКИ КОРАБЛЯ
Учебный год: 2007/2008
Семестр: весенний
Группа: 1310
КУРСОВАЯ РАБОТА
По дисциплине «ТЕХНИЧЕСКАЯ ФИЗИКА»
На тему «Расчет шпангоутной рамы сухогрузного судна методом угловых перемещений»
Дата выдачи задания: 11.03.2008
Срок выполнения:
Номер варианта исходных данных: ВII2
Исполнитель: студент Герасимов И.В.
Преподаватель: к.т.н., доцент Ипатовцев Ю.Н.
|
Дата сдачи работы |
Резолюция преподавателя |
_________________________ «______»_____________2008_г
__________________________
САНКТ-ПЕТЕРБУРГ
2008 г.
I.Исходные данные:
|
Вариант № В-II-4 |
|
|
Нагрузки |
|
|
Заделки |
|
|
Длины и жесткости стержней |
|
Таблица 1
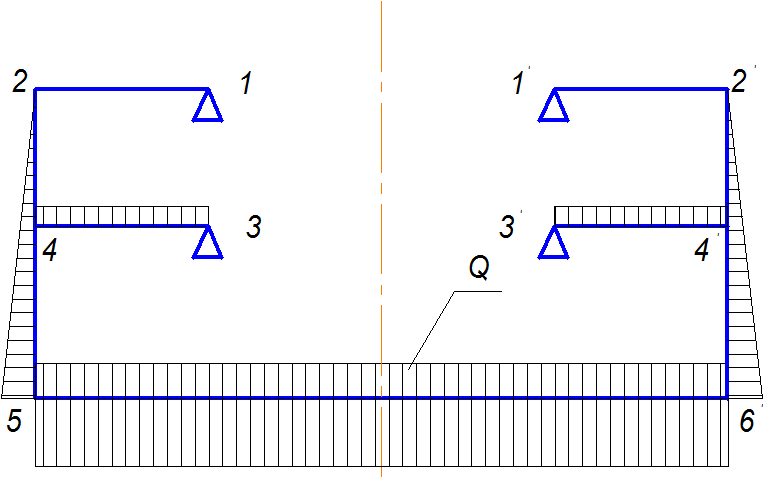
Рис. 1 Схема шпангоутной рамы
Введение
Прочность и сохранение формы поперечного сечения корпуса обеспечивается шпангоутными рамами. Большинство шпангоутных рам транспортных судов состоит из стержней, соединенных под прямым углом. Данный угол не меняется и в деформированном состоянии, так как узлы соединения, укрепленные кницами, обладают, как правило, весьма большой жесткостью по сравнению с изгибной жесткостью стержней рам. Как следствие, углы поворота узловых поперечных сечений стержней оказываются одинаковыми в каждом узле или, иначе говоря, у каждого узла имеется свой угол поворота.
Анализу прочности рамы предшествует раскрытие ее статической неопределимости, выполняемое методом сил или перемещений.
Значительно более распространенным типом шпангоутной рамы является сложная рама, в узлах которой сходится более двух стержней. Расчет таких рам целесообразно выполнять методом угловых перемещений, где в качестве неизвестных принимают углы поворота узлов, а систему разрешающих уравнений составляют из условий равновесия узлов рамы под действием приложенных к ним моментов.
1. Составление системы разрешающих уравнений:
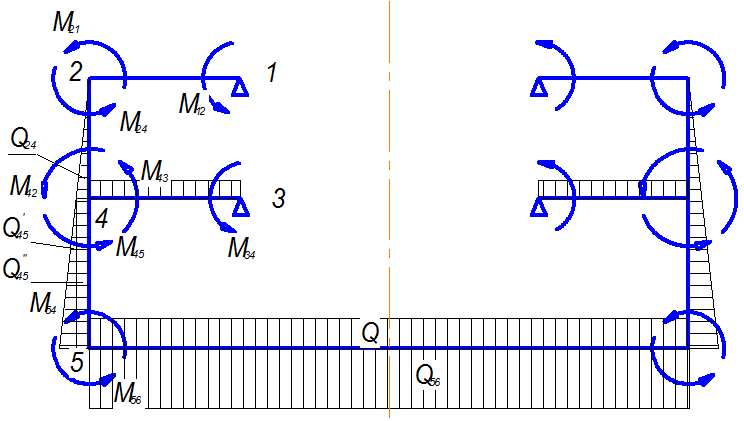
Рис.2 Направления узловых моментов
Учитывая симметрию рамы, рассмотрим только ее часть слева от ДП
![]()
![]()
![]()
![]()
![]()
2.Определение коэффициентов ![]() для всех стержней рамы:
для всех стержней рамы:
Любой опорный момент выражается в виде ![]() , где
, где ![]() ,
, 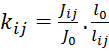 , значения которого приведены в
таблицу 2
, значения которого приведены в
таблицу 2
Таблица 2
|
Значения коэффициента |
|||||
|
Стержень |
1-2 |
2-4 |
3-4 |
4-5 |
5-6 |
|
|
10 |
4 |
10 |
32 |
100 |
3.Найти опорные моменты от пролетной
нагрузки ![]() , рассматривая стежни
рамы жестко заделанным по концам:
, рассматривая стежни
рамы жестко заделанным по концам:
Формулы для вычисления ![]() получены из справочника [1] и
приведены в таблицу 3.
получены из справочника [1] и
приведены в таблицу 3.
Таблица 3
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Вычисление значений ![]()
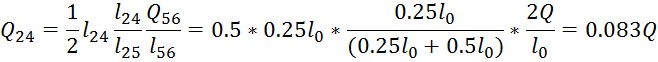
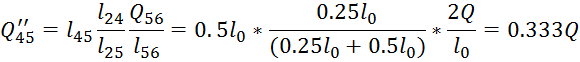
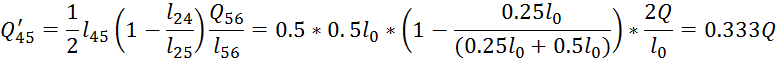
5.Решить систему уравнений:
Уравнения 1,2,3,4,5 переписаны следующими :
![]() .
.![]()
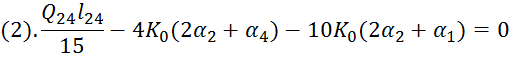
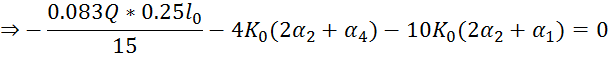
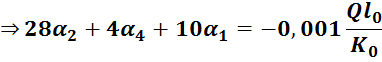
![]() .
.
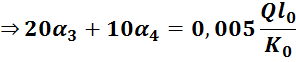
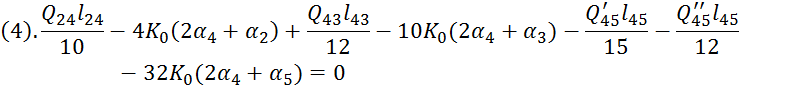
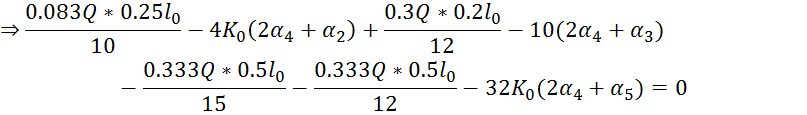
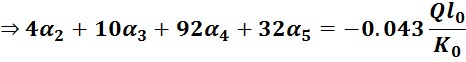
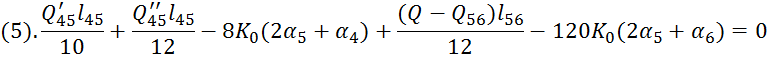
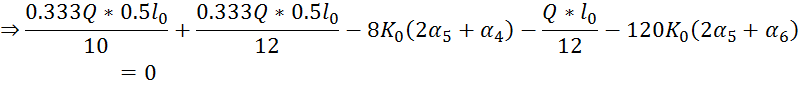
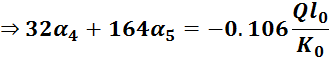
Тогда система уравнений для определения углов поворота имеет вид:
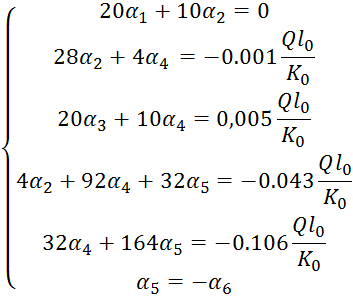
Решение этой системы:
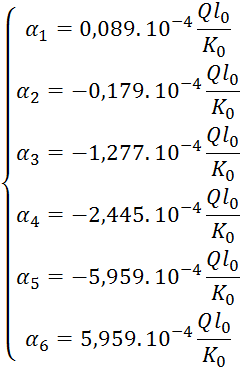
6.Определить узловые и опорные моменты:
Узловые моменты вычисленные следующим образом :
![]()
![]()
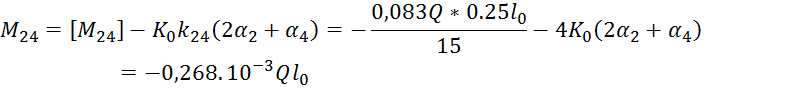
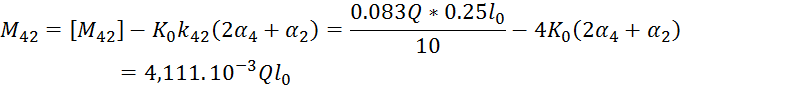
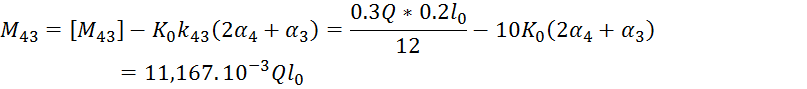
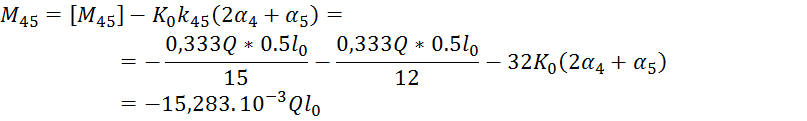
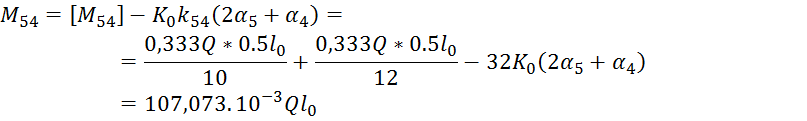
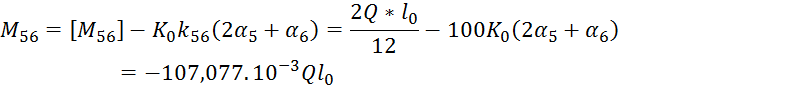
7.Проверим результаты вычисления :
![]()
![]()
![]()
8.Определение перерезывающих сил, изгибающих моментов и построение их эпюр:
Истинное направление опорных и узловых моментов изображено на рис.3
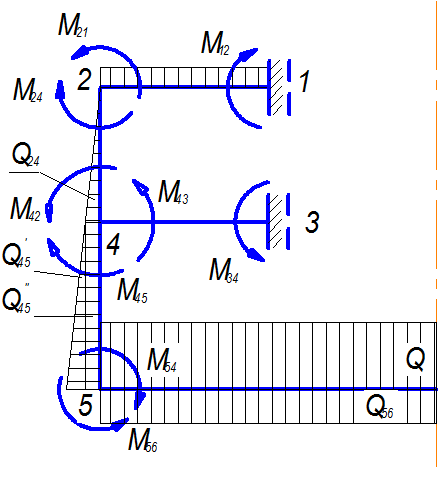
Рис.3 Истинное направление опорных и узловых моментов.
Определение опорных реакций и максимальных моментов от нагрузки:
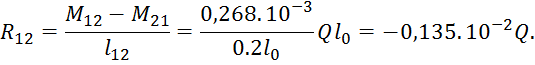
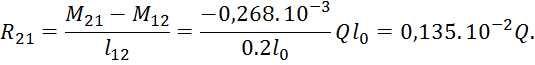
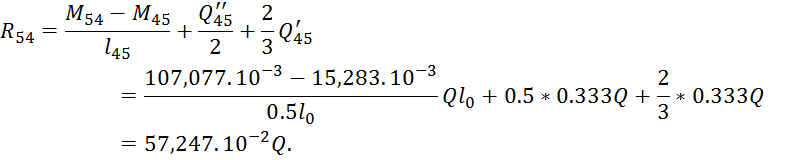
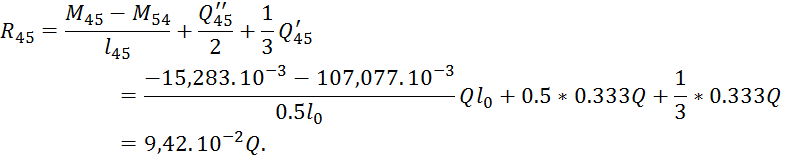
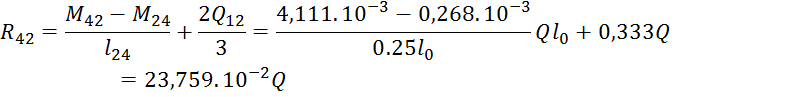
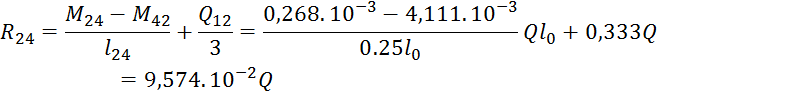
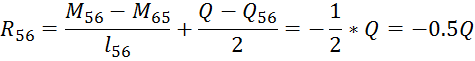
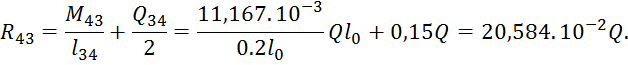
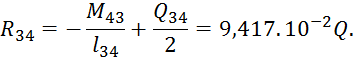
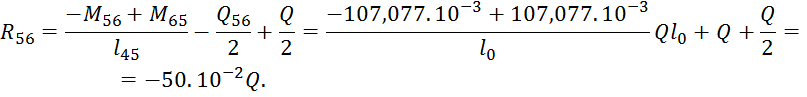
![]()
![]()
Рис.4 Эпюра изгибающих моментов
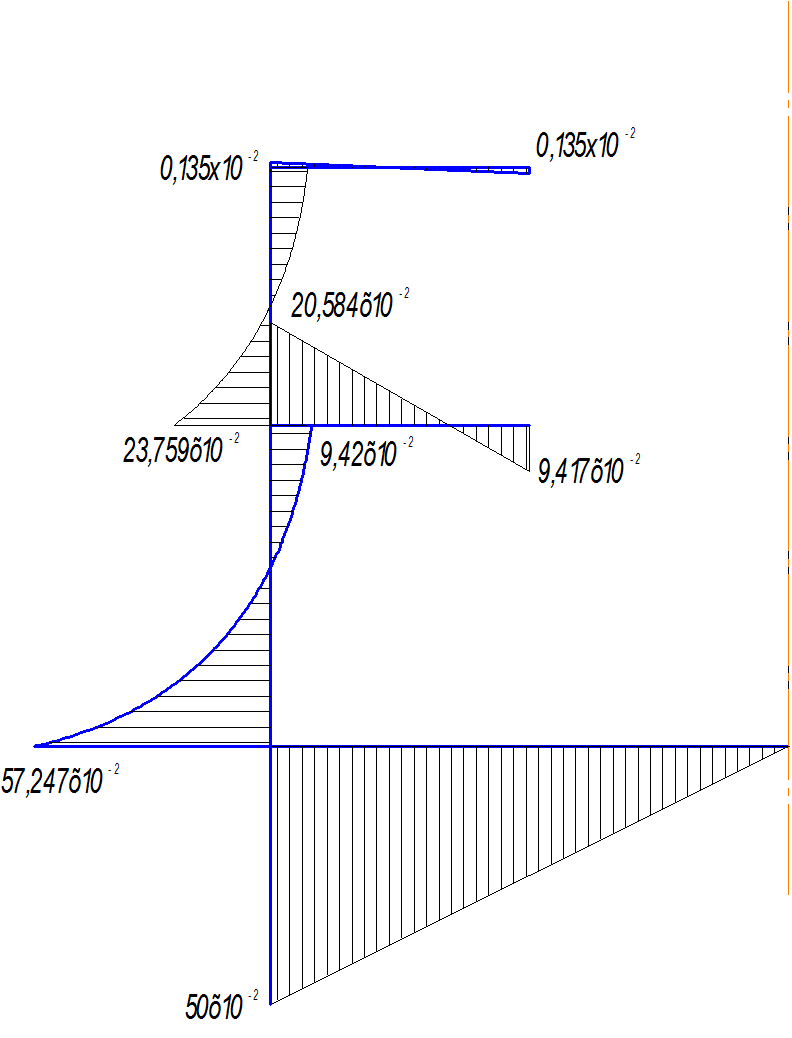
Рис.5 Эпюра изгибающих моментов
9.Упращенный расчет:
Рассмотрим балку 2-4-5,опирающуюся на жесткую опору 4 и упругие заделки 2,5(рис. 7)
Определим коэффициенты податливости для заделок 2 и 5
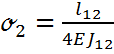 ,
,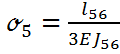
Система разрешающих уравнений:
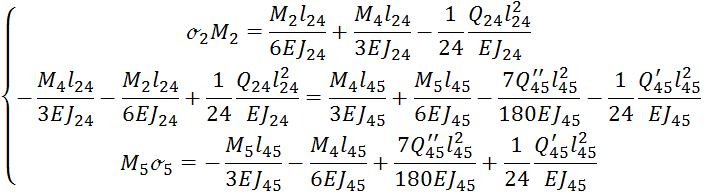
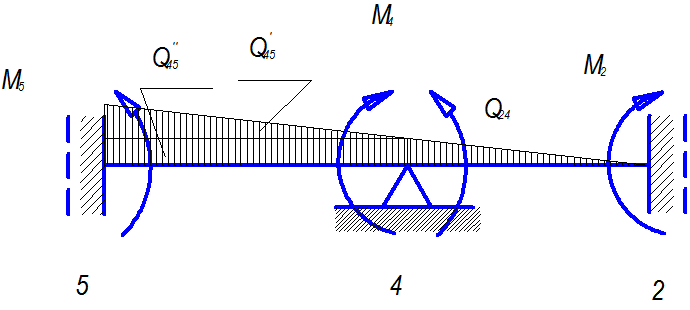
Рис. 6 К упрощенному расчету
Поставим значения и получим следующую каноническую систему:
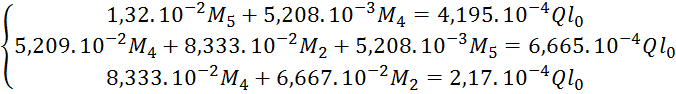
Решения этой системы :
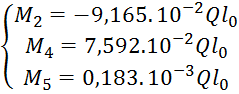
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.