Сложение и вычитание синусоидальных функций времени на комплексной плоскости. Векторная диаграмма

27 Сложение и вычитание синусоидальных функций времени на

комплексной плоскости. Векторная диаграмма.

Любую гармонически изменяющуюся во времени величину можно представить в виде функции

,

где I_m – амплитуда этой функции, T – ее период, ω – круговая частота и φ – сдвиг фазы. График такой функции выглядит следующим образом.

В электротехнике для оценки гармонических функций (в данном случае тока) используются следующие характеристики.

Среднее значение

Действующее, эффективное, среднее значение тока по тепловыделению

Поскольку операции с гармоническими функциями в явном виде весьма затруднительны, на практике используется представление синусоидально изменяющихся функций в виде вектора на комплексной плоскости. Исходную функцию времени называют оригиналом, а вектор на комплексной плоскости – ее изображением.

Сложение и вычитание синусоидальных функций

Пусть имеются две гармонические функции  и .

Требуется найти функцию i = i₁ + i₂, которая будет представлять собой гармоническую функцию с той же частотой.

Найдем изображения исходных функций на комплексной плоскости

После перехода от функции времени к изображениям – комплексным числам математические операции с ними становятся намного проще. Для сложения и вычитания, как правило, используется алгебраическая форма комплексных чисел, а для умножения, деления, возведения в степень и т.п. – показательная форма.

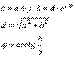
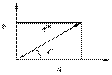
Переход от алгебраической формы комплексного числа к показательной

Примеры перевода из алгебраической формы в показательную