Синтез логических устройств

Синтез логических устройств.

Формы представления логических функций.

1. аналитическая запись.

f(x,y) = x + = x·y + x· +

f – функция

x,y – аргументы

x·y  - минтерм

x +  - макстерм

Минтерм – булево (логическое) произведение всех переменных (аргументов) каждая из которых входит в это произведение один раз.

Макстерм – булева сумма всех аргументов функции, каждая из которых входит в эту сумму один раз.

Для функции двух переменных:

Минтерм – m₀ = ,  m₁ = , m₂ = x·, m₃ = x·y

Макстерм – M₀ = +

Если есть инверсия, то в этой позиции 0, если нету, то 1.

Есть полные минтермы и макстермы, а есть и не полные.

Для функции трех переменных:

m₂ =

M =

2. с помощью карт Вейча или Карно.

Первыми появились карты Вейча.

Для функции двух переменных:      x + = сумме закрашенных слагаемых

	x
y	x·y
	x·

Другая запись:

	x
y	1
	1	1

Функция трех переменных:

	x	x
y
		z	z

Функция четырех переменных:

	x	x
y
y					w
					w
		z	z

3. таблица.

     Функция трех переменных:

i	x	y	z	f
0	0	0	0	1
1	0	0	1	0
2	0	1	0	0
3	0	1	1	1
4	1	0	0	1
5	1	0	1	0
6	1	1	0	0
7	1	1	1	1

i – порядковый номер минтерма

f = m₀·1 + m₁·0 + m₂·0 + m₃·1 + m₄·1 + m₅·0 + m₆·0 + m₇·1 = m₀ + m₃ + m₄ + m₇

 

 

Свойства минтермов и макстермов.

• Существуют одноименные минтермы и макстермы. Это те минтермы и макстермы, в которые входят противоположные переменные.

m₂ =

M₅ = x +  + z

Если n переменных, то (2ⁿ – 1) это сумма индексов у одноименных минтермов и макстермов.

• Булева сумма всех минтермов любого числа равна 1.

Булево произведение всех макстермов равно 0.

                                                     

• Произведение минтермов с разными индексами равно 0

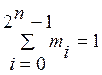
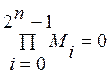
         m_i·m_j = 0

• Сумма макстермов с разными индексами равна 1

                        M_i + M_j = 1

Представление функций в совершенно нормальных формах.

Совершенно нормальная дизъюнктивная форма (СНДФ) -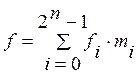

Совершенно нормальная конъюнктивная форма (СНКФ) -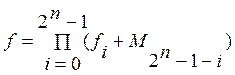

НДФ – здесь используется произведение переменных, в которых присутствуют не все переменные.

Пример НДФ: f(x₁, x_2, x₃) = x₁ +

Нужно перейти к СНДФ. Есть несколько способов это сделать:

1. составить таблицу функций и расписать.
2. каждый член умножить на комбинацию (х_i + ), где i – отсутствующий индекс в этом произведении.

 (х_i + )=1

f(x₁, x_2, x₃) = x₁ + =  x₁·()·() + ·() =

В основном всегда стремятся перейти от СНДФ к НДФ.

Упрощение булевых функций.

1.  использование тождеств.

2.  применение карт Карно, Вейча.

f = +

это СНДФ.

Здесь 32 переменных, 24 умножений, 7 сложений.

Представим функцию в виде карты минтермов (Вейча).

	A	A
B	1	1		1
B	1	1		1	D
					D
	1			1
		C	C

Чем больше объединений единиц, тем меньше количество переменных.

Чем меньше букв в произведении, тем проще электрическая схема.

   f =

Правила объединений: 

• соседние квадратики можно “склеить”.
• Квадраты, состоящие из четырех можно объединять.
• Двойные квадраты можно объединять.
• Полные строки и столбцы тоже можно объединять.
• Минтермы, которые находятся на концах строк или столбцов, объединяются.

Нарисуем электрическую схему для этой функции (рис. 1).

Схема получается гораздо проще, чем если бы мы рисовали для первоначальной функции.

                                  

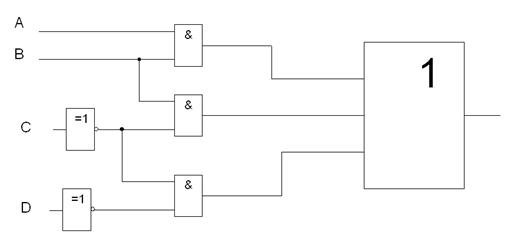
Рис. 1.

Использование избыточных комбинаций для упрощений.

Избыточные комбинации – комбинации, которые в коде не участвуют, и возникнуть не могут.

Допустим для кода 8421: 10 используют, а существует 16.

Не используются в коде: 1010, 1011, 1100, 1101, 1110, 1111

Пример:  f =

	1	☺
1☺
☺	☺	1	1

Если функция не имеет избыточных комбинаций, то функцию больше упростить нельзя. Предположим, что у функции есть избыточные комбинации: , , , отметим их в таблице ☺

                                                     ☺ поглощает 1

                                                     Вместо ☺ ставим либо 0, либо 1

              f =

Преобразование нескольких функций одновременно.

Преобразователь – переводит один код в другой (рис. 2).

                     

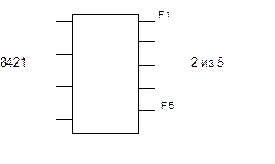
                                         Рис. 2.

Функция – логическое состояние, которое характеризуется на выходе цифрового устройства.

Если на выходе несколько функций:

Для каждой функции пишем формулу, минимизируем и создаем устройство, либо одновременно упрощаем все функции.

Пример:  f₁ =

                 f₂ =

                 f₃ =

	A	A
B		1
B	1			1	D
			1	1	D
		1		1
		C	C

 для f₁:

	A	A
B	1			1
B	1		1	1	D
			1	1	D
		C	C

 Для f₂:

Для f₃:

	A	A
B	1
B	1			1	D
	1	1	1	1	D
				1
		C	C

31 буква и 11 слагаемых

Проведем одновременную минимизацию:

1.  объединяем 1

2.  на каждой карте получаем одинаковую функцию.

E =

                  f₁ = E+

                 f₂ = E+

                 f₃ = E+

24 буквы и 9 слагаемых